The JEE Main 2022 July 25 – Shift 1 Maths Question Paper with Solutions is given on this page. Students can check the JEE Main 2022 answer keys here. They are advised to solve and practise JEE Main 2022 question papers so that they can be familiar with the type of questions asked for the JEE Main exam. Revising JEE Main 2022 question papers is the best method to prepare for the upcoming JEE Main exam.
JEE Main 2022 July 25th Shift 1 Mathematics Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. The total number of functions, f : {1, 2, 3, 4} → {1, 2, 3, 4, 5, 6} such that f(1) + f(2) = f(3), is equal to
(A) 60
(B) 90
(C) 108
(D) 126
Answer (B)
Sol. Case 1:If f(3) = 3 then f(1) and f(2) take 1 OR 2
No. of ways = 2⋅6 = 12
Case 2: If f(3) = 5 then f(1) and f(2) take 2 OR 3
OR 1 and 4
No. of ways = 2⋅6⋅2 = 24
Case 3: If f(3) = 2 then f(1) = f(2) = 1
No. of ways = 6
Case 4: If f(3) = 4 then f(1) = f(2) = 2
No. of ways = 6
OR f(1) and f(2) take 1 and 3
No. of ways = 12
Case 5: If f(3) = 6 then f(1) = f(2) = 3 ⇒ 6 ways
OR f(1) and f(2) take 1 and 5 ⇒ 12 ways
OR f(2) and f(1) take 2 and 4 ⇒ 12 ways
2. If α, β, γ, δ are the roots of the equation x4 + x3 + x2 + x + 1 = 0, then α2021 + β2021 + γ2021 + δ2021 is equal to
(A) –4
(B) –1
(C) 1
(D) 4
Answer (B)
Sol. \(\begin{array}{l}x^4 + x^3 + x^2 + x + 1 = 0\ OR\ \frac{x^5-1}{x-1}=0\left(x \neq 1\right) \end{array} \)
\(\begin{array}{l}\text{So roots are}~ e^{i2\pi/5},e^{i4\pi/5},e^{i6\pi/5},e^{i8\pi/5}\end{array} \)
i.e.α, β, γ and δ
From properties of nth root of unity
\(\begin{array}{l} 1^{2021}+\alpha^{2021}+\beta^{2021}+\gamma^{2021}+\delta^{2021}=0 \end{array} \)
\(\begin{array}{l} \Rightarrow\ \alpha^{2021}+\beta^{2021}+\gamma^{2021}+\delta^{2021}=-1\end{array} \)
3. For n ∈ N let \(\begin{array}{l} S_n=\left\{z\in C\colon |z-3+2i|=\frac{n}{4} \right\} \text{and}~ T_n=\left\{ z\ \in\ C \colon \left|z-2+3i\right|=\frac{1}{n}\right\}\end{array} \)
. Then the number of elements in the set \(\begin{array}{l} \left\{n\ \in\ N: S_n\cap T_n=\phi \right\}\end{array} \)
is
(A) 0
(B) 2
(C) 3
(D) 4
Answer (*)
Sol.
\(\begin{array}{l} S_n=\left\{z\ \in\ C:\left|z-3+2i\right|=\frac{n}{4} \right\} \end{array} \)
represents a circle with centre C1(3, –2) and radius \(\begin{array}{l} r_1=\frac{n}{4} \end{array} \)
Similarly Tn represents circle with centre C2(2, –3) and radius
\(\begin{array}{l} r_2=\frac{1}{n}\end{array} \)
As Sn ∩ Tn = φ
C1C2>r1 + r2 OR C1C2< |r1 – r2|
\(\begin{array}{l} \sqrt{2}>\frac{n}{4}+\frac{1}{n} \end{array} \)
OR
\(\begin{array}{l} \sqrt{2}<\left|\frac{n}{4}-\frac{1}{n}\right| \end{array} \)
n = 1, 2, 3, 4 n may take infinite values.
4. The number of q∈ (0, 4π) for which the system of linear equations
3(sin 3θ) x – y + z = 2
3(cos 2θ) x + 4y + 3z = 3
6x + 7y + 7z = 9
has no solution, is
(A) 6
(B) 7
(C) 8
(D) 9
Answer (B)
Sol.
\(\begin{array}{l} \Delta = \begin{vmatrix}3\sin 3\theta & -1 & 1 \\3\cos 2\theta & 4 & 3 \\6 & 7 & 7 \\\end{vmatrix} \end{array} \)
= 3sin3θ(7) + 1(21cos2θ – 18) + 1(21cos2θ – 24)
Δ = 21sin3θ + 42cos2θ – 42
For no solution
sin3θ + 2cos2θ = 2
⇒ sin3θ = 2⋅2sin2θ
⇒ 3sinθ – 4sin3θ = 4sin2θ
⇒ sinθ(3 – 4sinθ – 4sin2θ) = 0
\(\begin{array}{l}sin\theta = 0\ OR\ sin\theta = \frac{1}{2} \end{array} \)
\(\begin{array}{l} \theta=\pi, 2\pi,3\pi,\frac{\pi}{6},\frac{5\pi}{6},\frac{13\pi}{6},\frac{17\pi}{6} \end{array} \)
5. If \(\begin{array}{l} \displaystyle \lim_{n\rightarrow\infty}\left(\sqrt{n^2-n-1}+n\alpha+\beta\right)=0 \end{array} \)
then 8(α + β) is equal to
(A) 4
(B) –8
(C) –4
(D) 8
Answer (C)
Sol.
\(\begin{array}{l} \displaystyle \lim_{n\rightarrow\infty}\left(\sqrt{n^2-n-1}+n\alpha+\beta\right)=0 \end{array} \)
\(\begin{array}{l} =\displaystyle \lim_{n\rightarrow\infty}n\left[\sqrt{1-\frac{1}{n}-\frac{1}{n^2}}+\alpha+\frac{\beta}{n}\right]=0\end{array} \)
∴ α = –1
Now,
\(\begin{array}{l} \displaystyle \lim_{n\rightarrow\infty}n\left[\left\{1-\left(\frac{1}{n}+\frac{1}{n^2}\right) \right\}^{\frac{1}{2}}+\frac{\beta}{n}-1\right]=0\end{array} \)
\(\begin{array}{l} \displaystyle \lim_{n\rightarrow\infty}n\frac{\left(1-\frac{1}{2}\left(\frac{1}{n}+\frac{1}{n^2}\right)+\dots\right)+\frac{\beta}{n}-1}{\frac{1}{n}}=0\end{array} \)
\(\begin{array}{l} \Rightarrow\ \beta – \frac{1}{2}=0 \end{array} \)
\(\begin{array}{l} \therefore \beta = \frac{1}{2}\end{array} \)
Now,
\(\begin{array}{l} 8\left(\alpha+\beta\right)=8\left(-\frac{1}{2}\right)=-4\end{array} \)
6. If the absolute maximum value of the function \(\begin{array}{l} f(x) = (x^2 – 2x + 7) e^{(4x^3-12x^2-180x + 31)} \end{array} \)
in the interval [–3, 0] is f(α), then
(A) α = 0
(B) α = –3
(C) α∈ (–1, 0)
(D) α∈ (–3, –1]
Answer (B)
Sol. Given,
\(\begin{array}{l} f\left(x\right)=\underset{f_1\left(x\right)}{\underbrace{\left(x^2-2x+7\right)}}\ \underset{f_2\left(x\right)}{\underbrace{e^{\left(4x^3-12x^2-180x+31\right)}}}\end{array} \)
f1(x) = x2 – 2x + 7
\(\begin{array}{l} f’_1\left(x\right)=2x-2,\end{array} \)
so f(x) is decreasing in [–3, 0]
and positive also
\(\begin{array}{l} f_2\left(x\right)=e^{4x^3-12x^2-180x+31} \end{array} \)
\(\begin{array}{l} f_2^{‘}\left(x\right)=e^{4x^3-12x^2-180x+31} . 12x^2 – 24x – 180\end{array} \)
\(\begin{array}{l} =12\left(x-5\right)\left(x+3\right)e^{4x^3-12x^2-180x+31}\end{array} \)
So, f2(x) is also decreasing and positive in {–3, 0}
∴ absolute maximum value of f(x) occurs at x = –3
∴ α = -3
7. The curve y(x) = ax3 + bx2 + cx + 5 touches the x-axis at the point P(–2, 0) and cuts the y-axis at the point Q, where y′ is equal to 3. Then the local maximum value of y(x) is
\(\begin{array}{l} (\text{A})\ \frac{27}{4} \end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{29}{4} \end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{37}{4} \end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{9}{2} \end{array} \)
Answer (A)
Sol. f(x) = y = ax3 + bx2 + cx + 5 …(i)
\(\begin{array}{l} \frac{dy}{dx}= 3ax^2 + 2bx + c ……\left(ii\right )\end{array} \)
Touches x-axis at P(–2, 0)
\(\begin{array}{l} \Rightarrow y\left|_{x=-2}\right.=0\Rightarrow-8a+4b-2c+5=0\dots\left(iii\right) \end{array} \)
Touches x-axis at P(–2, 0) also implies
\(\begin{array}{l} \frac{dy}{dx}\left|_{x=-2}\right.=0\Rightarrow 12a-4b+c=0\dots\left(iv\right) \end{array} \)
y = f(x) cuts y-axis at (0, 5)
Given,
\(\begin{array}{l} \frac{dy}{dx}\left.\right|_{x=0}=c=3\dots\left(v\right)\end{array} \)
From (iii), (iv) and (v)
\(\begin{array}{l} a=-\frac{1}{2},b=-\frac{3}{4},c=3\end{array} \)
\(\begin{array}{l} \Rightarrow f\left(x\right)=\frac{-x^2}{2}-\frac{3}{4}x^2+3x+5\end{array} \)
\(\begin{array}{l} f’\left(x\right)=\frac{-3}{2}x^2-\frac{3}{2}x+3\end{array} \)
\(\begin{array}{l} =\frac{-3}{2}\left(x+2\right)\left(x-1\right) \end{array} \)
f′(x) = 0 at x = –2 and x = 1
By first derivative test x = 1 in point of local maximum
Hence local maximum value of f(x) is f(1)
\(\begin{array}{l} i.e.,\frac{27}{4} \end{array} \)
8. The area of the region given by
\(\begin{array}{l} A=\left\{\left(x,y\right);x^2\leq y \leq \text{min}\left\{x+2, 4-3x \right\} \right\}\end{array} \)
is
\(\begin{array}{l} (\text{A})\ \frac{31}{8}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{17}{6}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{19}{6}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{27}{8}\end{array} \)
Answer (B)
Sol. A = {(x, y) : x2 ≤ y ≤ min {x + 2, 4 – 3x}
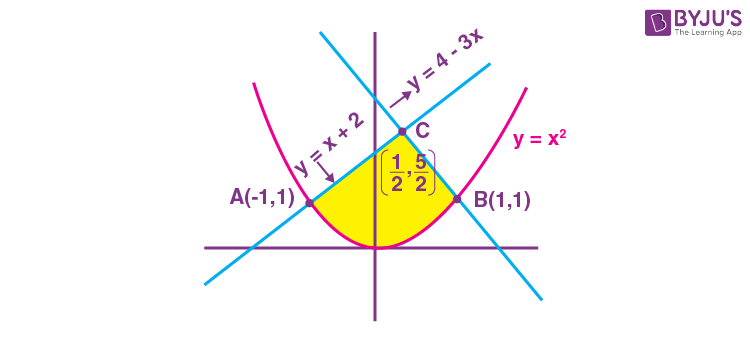
So, area of the required region
\(\begin{array}{l} A=\displaystyle\int\limits_{-1}^{\frac{1}{2}}\left(x+2-x^2\right)dx+\displaystyle\int\limits_{\frac{1}{2}}^{1}\left(4-3x-x^2\right)dx\end{array} \)
\(\begin{array}{l} =\left[\frac{x^2}{2}+2x-\frac{x^3}{3}\right]_{-1}^{\frac{1}{2}}+\left[4x-\frac{3x^2}{2}-\frac{x^3}{3}\right]_\frac{1}{2}^1 \end{array} \)
\(\begin{array}{l} =\left(\frac{1}{8}+1-\frac{1}{24}\right)-\left(\frac{1}{2}-2+\frac{1}{3}\right)+\left(4-\frac{3}{2}-\frac{1}{3}\right)-\left(2-\frac{3}{8}-\frac{1}{24}\right)\end{array} \)
\(\begin{array}{l} =\frac{17}{6} \end{array} \)
9. For any real number x, let [x] denote the largest integer less than equal to x. Let f be a real valued function defined on the interval [–10, 10] by \(\begin{array}{l} f\left(x\right)=\left\{\begin{matrix}x-[x], \text{ if } [x] \text{ is odd} \\1+[x]-x, \text{if }[x]\text{ is even}\end{matrix}\right.\end{array} \)
Then the value of \(\begin{array}{l} \frac{\pi^2}{10}\displaystyle\int\limits_{-10}^{10}f\left(x\right)\cos\pi x\ dx\end{array} \)
is
(A) 4
(B) 2
(C) 1
(D) 0
Answer (A)
Sol.
\(\begin{array}{l} f\left(x\right)=\left\{\begin{matrix}x-[x],\ \text{if }[x]\text{ is odd} \\1+[x]-x, \text{if }[x]\text{ is even}\end{matrix}\right.\end{array} \)
Graph of f(x)
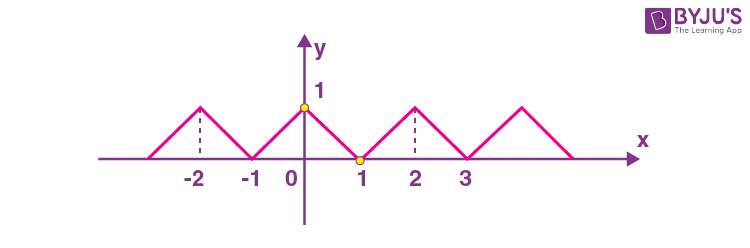
So,
\(\begin{array}{l} \frac{\pi^2}{10}\displaystyle\int\limits_{-10}^{10}f\left(x\right)\cos\ \pi x\ dx=\frac{\pi^2}{10}\cdot 20\displaystyle\int\limits_0^1 f\left(x\right)\cos\pi x\ dx \end{array} \)
\(\begin{array}{l} =2\pi^2\displaystyle\int\limits_0^1\left(1-x\right)\cos\pi x\ dx \end{array} \)
\(\begin{array}{l} =2\pi^2\left\{\left.\left(1-x\right)\frac{\sin\pi x}{\pi}\right|_0^1 -\left.\frac{\cos\pi x}{\pi^2}\right|_0^1\right\}=4\end{array} \)
10. The slope of the tangent to a curve C : y = y(x) at any point (x, y) on it is \(\begin{array}{l} \frac{2e^{2x}-6e^{-x}+9}{2+9e^{-2x}}\end{array} \)
. If C passes through the points \(\begin{array}{l} \left(0, \frac{1}{2}+\frac{\pi}{2\sqrt{2}}\right)\text{ and }\left(\alpha,\frac{1}{2}e^{2\alpha}\right),\end{array} \)
then eα is equal to
\(\begin{array}{l} (\text{A})\ \frac{3+\sqrt{2}}{3-\sqrt{2}} \end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{3}{\sqrt{2}}\left(\frac{3+\sqrt{2}}{3-\sqrt{2}} \right)\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{1}{\sqrt{2}}\left(\frac{\sqrt{2}+1}{\sqrt{2}-1} \right)\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{\sqrt{2}+1}{\sqrt{2}-1}\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} \frac{dy}{dx}=\frac{2e^{2x}-6e^{-x}+9}{2+9e^{-2x}}=e^{2x}-\frac{6e^{-x}}{2+9e^{-2x}}\end{array} \)
\(\begin{array}{l} \int dy=\int e^{2x}dx-3\int \frac{e^{-x}}{\underset{\text{put }e^{-x}=t}{\underbrace{1+\left(\frac{3e^{-x}}{\sqrt{2}}\right)^2}}}dx\end{array} \)
\(\begin{array}{l} =\frac{e^{2x}}{2}+3\int\frac{dt}{1+\left(\frac{3t}{\sqrt{2}}\right)^2} \end{array} \)
\(\begin{array}{l} =\frac{e^{2x}}{2}+\sqrt{2}\tan^{-1}\frac{3t}{\sqrt{2}}+C \end{array} \)
\(\begin{array}{l} y=\frac{e^{2x}}{2}+\sqrt{2}\tan^{-1}\left(\frac{3e^{-x}}{\sqrt{2}}\right)+C \end{array} \)
It is given that the curve passes through
\(\begin{array}{l} \left(0,\frac{1}{2}+\frac{\pi}{2\sqrt{2}}\right)\end{array} \)
\(\begin{array}{l} \frac{1}{2}+\frac{\pi}{2\sqrt{2}}=\frac{1}{2}+\sqrt{2}\tan^{-1}\left(\frac{3}{\sqrt{2}}\right)+C\end{array} \)
\(\begin{array}{l} \Rightarrow C=\frac{\pi}{2\sqrt{2}}-\sqrt{2}\tan^{-1}\left(\frac{3}{\sqrt{2}}\right) \end{array} \)
Now if
\(\begin{array}{l} \left(\alpha,\frac{1}{2}e^{2\alpha}\right)\end{array} \)
satisfies the curve, then
\(\begin{array}{l} \frac{1}{2}e^{2\alpha}=\frac{e^{2\alpha}}{2}+\sqrt{2}\tan^{-1}\left(\frac{3e^{-\alpha}}{\sqrt{2}}\right)+\frac{\pi}{2\sqrt{2}}-\sqrt{2}\tan^{-1}\left(\frac{3}{\sqrt{2}}\right)\end{array} \)
\(\begin{array}{l} \tan^{-1}\left(\frac{3}{\sqrt{2}}\right)-\tan^{-1}\left(\frac{3e^{-\alpha}}{\sqrt{2}}\right)=\frac{\pi}{2\sqrt{2}}\times\frac{1}{\sqrt{2}}=\frac{\pi}{4}\end{array} \)
\(\begin{array}{l} \frac{\frac{3}{\sqrt{2}}-\frac{3e^{-\alpha}}{\sqrt{2}}}{1+\frac{9}{2}e^{-\alpha}}=1\end{array} \)
\(\begin{array}{l}\frac{3}{\sqrt{2}}e^\alpha-\frac{3}{\sqrt{2}}=e^\alpha+\frac{9}{2} \end{array} \)
\(\begin{array}{l} e^\alpha=\frac{\frac{9}{2}+\frac{3}{\sqrt{2}}}{\frac{3}{\sqrt{2}}-1}=\frac{3}{\sqrt{2}}\left(\frac{3+\sqrt{2}}{3-\sqrt{2}}\right)\end{array} \)
11. The general solution of the differential equation (x – y2)dx + y(5x + y2)dy = 0 is :
\(\begin{array}{l} (\text{A})\ \left(y^2+x\right)^4=C\left|\left(y^2+2x\right)^3\right|\end{array} \)
\(\begin{array}{l} (\text{B})\ \left(y^2+2x\right)^4=C\left|\left(y^2+x\right)^3\right|\end{array} \)
\(\begin{array}{l} (\text{C})\ \left|\left(y^2+x\right)^3\right|=C\left(2y^2+x\right)^4\end{array} \)
\(\begin{array}{l} (\text{D})\ \left|\left(y^2+2x\right)^3\right|=C\left(2y^2+x\right)^4\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l} \left(x-y^2\right)dx+y\left(5x+y^2\right)dy=0\end{array} \)
\(\begin{array}{l} y\frac{dy}{dx}=\frac{y^2-x}{5x+y^2} \end{array} \)
Let y2 = t
\(\begin{array}{l} \frac{1}{2}\cdot\frac{dt}{dx}=\frac{t-x}{5x+t} \end{array} \)
Now substitute, t = vx
\(\begin{array}{l} \frac{dt}{dx}=v+x\frac{dv}{dx}\end{array} \)
\(\begin{array}{l} \frac{1}{2}\left\{v+x\frac{dv}{dx} \right\}=\frac{v-1}{5+v}\end{array} \)
\(\begin{array}{l} x\frac{dv}{dx}=\frac{2v-2}{5+v}-v=\frac{-3v-v^2-2}{5+v}\end{array} \)
\(\begin{array}{l} \int\frac{5+v}{v^2+3v+2}dv=\int-\frac{dx}{x} \end{array} \)
\(\begin{array}{l} \int\frac{4}{v+1}dv-\int\frac{3}{v+2}dv=-\int\frac{dx}{x}\end{array} \)
\(\begin{array}{l} 4\text{In}\left|v+1\right|-3\text{In}\left|v+2\right|=-\text{In }x+\text{In }C\end{array} \)
\(\begin{array}{l} \left|\frac{\left(v+1\right)^4}{\left(v+2\right)^3}\right|=\frac{C}{x}\end{array} \)
\(\begin{array}{l} \left|\frac{\left(\frac{y^2}{x}+1\right)^4}{\left(\frac{y^2}{x}+2\right)^3}\right|=\frac{C}{x}\end{array} \)
\(\begin{array}{l} \left|\left(y^2+x\right)^4\right|=C\left|\left(y^2+2x\right)^3\right|\end{array} \)
12. A line, with the slope greater than one, passes through the point A(4, 3) and intersects the line
x – y – 2 = 0 at the point B. If the length of the line segment AB is \(\begin{array}{l} \frac{\sqrt{29}}{3}, \ \text{then B also lies on the line :}\end{array} \)
(A) 2x + y = 9
(B) 3x – 2y = 7
(C) x + 2y = 6
(D) 2x – 3y = 3
Answer (C)
Sol.
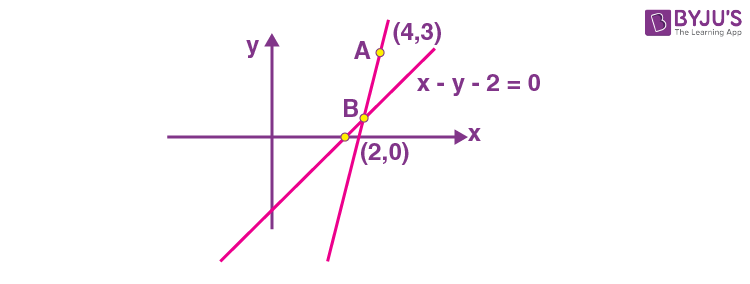
Let inclination of required line is θ,
So the coordinates of point B can be assumed as
\(\begin{array}{l} \left(4-\frac{\sqrt{29}}{3}\cos\theta, 3-\frac{\sqrt{29}}{3}\sin\theta\right) \end{array} \)
Which satisfices x – y – 2 = 0
\(\begin{array}{l} 4-\frac{\sqrt{29}}{3}\cos\theta-3+\frac{\sqrt{29}}{3}\sin\theta-2=0 \end{array} \)
\(\begin{array}{l} \sin\theta-\cos\theta=\frac{3}{\sqrt{29}}\end{array} \)
By squaring
\(\begin{array}{l} \sin 2\theta=\frac{20}{29}=\frac{2\tan\theta}{1+\tan^2\theta}\end{array} \)
\(\begin{array}{l} \tan\theta=\frac{5}{2}\text{ only (because slope is greater than 1)}\end{array} \)
\(\begin{array}{l} \sin\theta=\frac{5}{\sqrt{29}},\cos\theta=\frac{{2}}{\sqrt{29}} \end{array} \)
\(\begin{array}{l} Point~B:\left(\frac{10}{3},\frac{4}{3}\right)\end{array} \)
Which also satisfies x + 2y = 6
13. Let the locus of the centre (α, β), β> 0, of the circle which touches the circle x2 +(y – 1)2 = 1 externally and also touches the x-axis be L. Then the area bounded by L and the line y = 4 is :
\(\begin{array}{l} (\text{A})\ \frac{32\sqrt{2}}{3}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{40\sqrt{2}}{3}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{64}{3}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{32}{3}\end{array} \)
Answer (C)
Sol.
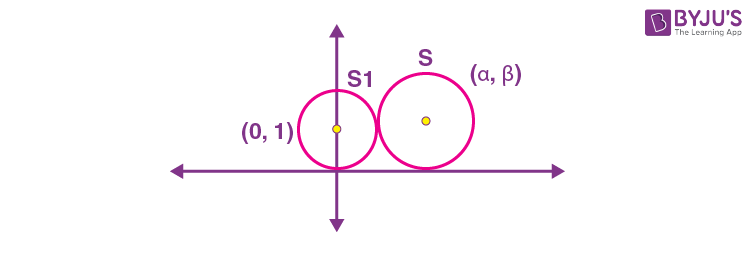
Radius of circle S touching x-axis and centre (α, β) is |β|. According to given conditions
α2 + (β – 1)2 = (|β| + 1)2
α2 + β2 – 2β + 1 = β2 + 1 + 2|β|
α2 = 4β as β> 0
∴ Required louse is L : x2 = 4y
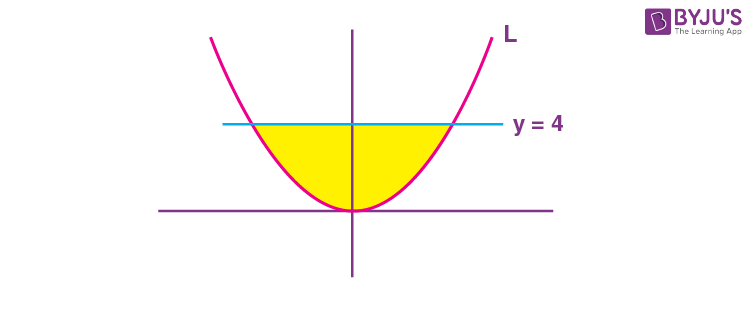
\(\begin{array}{l}\text{The area of shaded region }=2\int_0^42\sqrt{y}dy \end{array} \)
\(\begin{array}{l} =4\cdot\left[\frac{y^\frac{3}{2}}{\frac{3}{2}}\right]_0^4\end{array} \)
\(\begin{array}{l} =\frac{64}{3}\text{ square units}.\end{array} \)
14. Let P be the plane containing the straight line \(\begin{array}{l} \frac{x-3}{9}=\frac{y+4}{-1}=\frac{z-7}{-5}\end{array} \)
and perpendicular to the plane containing the straight lines \(\begin{array}{l} \frac{x}{2}=\frac{y}{3}=\frac{z}{5} \end{array} \)
and \(\begin{array}{l} \frac{x}{3}=\frac{y}{7}=\frac{z}{8}.\end{array} \)
If d is the distance P from the point (2, –5, 11), then d2 is equal to :
\(\begin{array}{l} (\text{A})\ \frac{147}{2}\end{array} \)
(B) 96
\(\begin{array}{l} (\text{C})\ \frac{32}{3}\end{array} \)
(D) 54
Answer (C*)
Sol. Let <a, b, c> be direction ratios of plane containing lines
\(\begin{array}{l} \frac{x}{2}=\frac{y}{3}=\frac{z}{5}\end{array} \)
and \(\begin{array}{l} \frac{x}{3}=\frac{y}{7}=\frac{z}{8}.\end{array} \)
∴ 2a + 3b + 5c = 0 …(i)
and 3a + 7b + 8c = 0 …(ii)
from eq. (i) and (ii)
\(\begin{array}{l} \frac{a}{24-35}=\frac{b}{15-16}=\frac{c}{14-9} \end{array} \)
∴ D.RS. of plane are < 11, 1, –5>
Let D.RS of plane P be <a1, b1, c1> then.
11a1 + b1 – 5c1 = 0 …(iii)
and 9a1 – b1 – 5c1 = 0 …(iv)
From eq. (iii) and (iv) :
\(\begin{array}{l} \frac{a_1}{-5-5}=\frac{b_1}{-45+55}=\frac{c_1}{-11-9} \end{array} \)
∴ D.A5. of plane P are < 1, –1, 2>
Equation plane P is : 1(x – 3) –1(y + 4) +2(z –7) = 0
⇒ x – y + 2z – 21 = 0
Distance from point (2, –5, 11) is
\(\begin{array}{l} d=\frac{\left|2+5+22-2\right|}{\sqrt{6}}\end{array} \)
\(\begin{array}{l} \therefore d^2=\frac{32}{3}\end{array} \)
15. Let ABC be a triangle such that \(\begin{array}{l} \overrightarrow{BC}=\overrightarrow{a},\overrightarrow{CA}=\overrightarrow{b},\overrightarrow{AB}=\overrightarrow{c},\left|\overrightarrow{a}\right|=6\sqrt{2},\left|\overrightarrow{b}\right|=2\sqrt{3}\end{array} \)
and \(\begin{array}{l} \overrightarrow{b}\cdot\overrightarrow{c}=12.\end{array} \)
Consider the statements :
\(\begin{array}{l} \left(S1\right):\left|\left(\overrightarrow{a}\times\overrightarrow{b}\right)+\left(\overrightarrow{c}\times\overrightarrow{b}\right)\right|-\left|\overrightarrow{c}\right|=6\left(2\sqrt{2}-1\right)\end{array} \)
\(\begin{array}{l} \left(S2\right):\angle ACB=\cos^{-1}\left(\sqrt{\frac{2}{3}}\right) \end{array} \)
Then
(A) Both (S1) and (S2) are true
(B) Only (S1) is true
(C) Only (S2) is true
(D) Both (S1) and (S2) are false
Answer (C*)
Sol.

\(\begin{array}{l}\because\ \vec{a}+\vec{b}+\vec{c}=0\cdots(i)\end{array} \)
then
\(\begin{array}{l} \vec{a}+\vec{c}=-\vec{b}\end{array} \)
then
\(\begin{array}{l} \left(\overrightarrow{a}+\overrightarrow{c}\right)\times\overrightarrow{b}=-\overrightarrow{b}\times\overline{b}\end{array} \)
\(\begin{array}{l} \therefore\ \vec{a}\times\vec{b}+\vec{c}\times\vec{b}=\vec{0}\cdots(ii)\end{array} \)
For
\(\begin{array}{l} \left(S1\right):\left|\vec{a}\times\vec{b}+\vec{c}\times\vec{b}\right|-\left|\vec{c}\right|=6\left(2\sqrt{2}-1\right)\end{array} \)
\(\begin{array}{l} \left|\left(\vec{a}+\vec{c}\right)\times\vec{b}\right|-\left|\vec{c}\right|=6\left(2\sqrt{2}-1\right)\end{array} \)
\(\begin{array}{l} \left|\vec{c}\right|=6-12\sqrt{2}\ \left(\text{not possible}\right)\end{array} \)
Hence (S1) is not correct
For (S2) : from (i)
\(\begin{array}{l} \vec{b}+\vec{c}=-\vec{a} \end{array} \)
\(\begin{array}{l} \Rightarrow\ \vec{b}\cdot\vec{b}+\vec{c}\cdot\vec{b}=-\vec{a}\cdot\vec{b}\end{array} \)
\(\begin{array}{l} \Rightarrow\ 12+12=-6\sqrt{2}\cdot2\sqrt{3}\cos\left(\pi-\angle ACB\right)\end{array} \)
\(\begin{array}{l} \therefore\ \cos\left(\angle ACB\right)=\sqrt{\frac{2}{3}}\end{array} \)
\(\begin{array}{l} \therefore\ \angle ACB=\cos^{-1}\sqrt{\frac{2}{3}}\end{array} \)
∴ S(2) is correct.
16. If the sum and the product of mean and variance of a binomial distribution are 24 and 128 respectively, then the probability of one or two successes is :
\(\begin{array}{l} (\text{A})\ \frac{33}{2^{32}} \end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{33}{2^{29}} \end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{33}{2^{28}} \end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{33}{2^{27}} \end{array} \)
Answer (C)
Sol. If n is number of trails, p is probability of success and q is probability of unsuccess then,
Mean = np and variance = npq.
Here np + npq = 24 …(i)
np.npq = 128 …(ii)
and q = 1 – p …(iii)
from eq. (i), (ii) and (iii) :
\(\begin{array}{l} p=q=\frac{1}{2}\end{array} \)
and n = 32.
∴ Required probability
\(\begin{array}{l} =P\left(X=1\right)+P\left(X=2\right) \end{array} \)
\(\begin{array}{l} =^{32}C_1\cdot\left(\frac{1}{2}\right)^{32}+^{32}C_2\cdot\left(\frac{1}{2}\right)^{32}\end{array} \)
\(\begin{array}{l} =\left(32+\frac{32\times 31}{2}\right)\cdot\frac{1}{2^{32}}\end{array} \)
\(\begin{array}{l} =\frac{33}{2^{28}}\end{array} \)
17. If the numbers appeared on the two throws of a fair six faced die are α and β, then the probability that x2 + αx + β> 0, for all x ∈ R, is :
\(\begin{array}{l} (\text{A})\ \frac{17}{36}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{4}{9}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{1}{2}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{19}{36}\end{array} \)
Answer (A)
Sol. For x2 + αx + β> 0 ∀ x∈R to hold, we should have α2 – 4β<0
If α = 1, β can be 1, 2, 3, 4, 5, 6 i.e., 6 choices
If α = 2, β can be 2, 3, 4, 5, 6 i.e., 5 choices
If α = 3, β can be 3, 4, 5, 6 i.e., 4 choices
If α = 4, β can be 5 or 6 i.e., 2 choices
If α = 6, No possible value for βi.e., 0 choices
Hence total favourable outcomes
= 6 + 5 + 4 + 2 + 0 + 0
= 17
Total possible choices for α and β = 6 × 6 = 36
Required probability
\(\begin{array}{l} =\frac{17}{36}\end{array} \)
18. The number of solutions of |cos x| = sinx, such that –4π ≤ x ≤ 4π is :
(A) 4
(B) 6
(C) 8
(D) 12
Answer (C)
Sol. Number of solutions of the equation |cosx| = sinx for x ∈ [-4π, 4π] will be equal to 4 times the number of solutions of the same equation for x∈[0, 2π].
Graphs of y = |cosx| and y = sinx are as shown below.
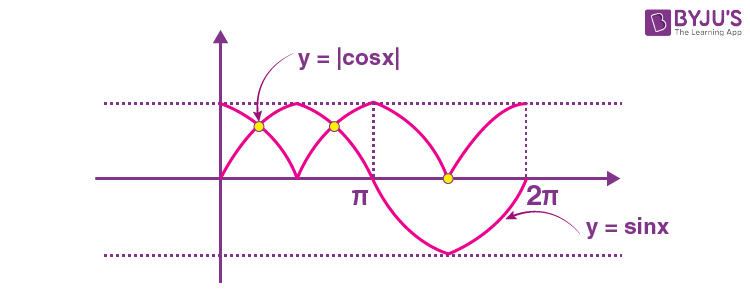
Hence, two solutions of given equation in [0, 2π]
⇒ Total of 8 solutions in [–4π, 4π].
19. A tower PQ stands on a horizontal ground with base Q on the ground. The point R divides the tower in two parts such that QR = 15 m. If from a point A on the ground the angle of elevation of R is 60° and the part PR of the tower subtends an angle of 15° at A, then the height of the tower is :
\(\begin{array}{l} (\text{A})\ 5\left(2\sqrt{3}+3\right)\text{ m}\end{array} \)
\(\begin{array}{l} (\text{B})\ 5\left(\sqrt{3}+3\right)\text{ m}\end{array} \)
\(\begin{array}{l} (\text{C})\ 10\left(\sqrt{3}+1\right)\text{ m}\end{array} \)
\(\begin{array}{l} (\text{D})\ 10\left(2\sqrt{3}+1\right)\text{ m}\end{array} \)
Answer (A)
Sol.
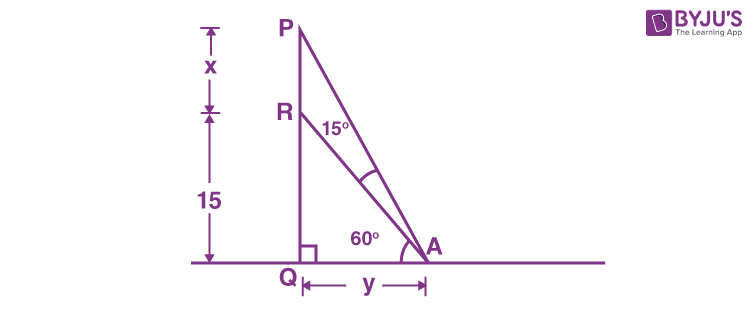
\(\begin{array}{l}From \triangle APQ\\ \frac{x+15}{y}=\tan75^\circ\cdots(i) \end{array} \)
\(\begin{array}{l}From \triangle RQA\\ \frac{15}{y}=\tan60^\circ\cdots(ii) \end{array} \)
From (i) and (ii)
\(\begin{array}{l} \frac{x+15}{15}=\frac{\tan75^\circ}{\tan60^\circ}=\frac{\tan\left(45^\circ+30^\circ\right)}{\tan60^\circ}=\frac{\sqrt{3}+1}{\left(\sqrt{3}-1\right)\cdot\sqrt{3}} \end{array} \)
On simplification,
\(\begin{array}{l} x=10\sqrt{3}\text{ m}\end{array} \)
Hence height of the tower
\(\begin{array}{l} =\left(15+10\sqrt{3}\right)\text{ m}\end{array} \)
\(\begin{array}{l} =5\left(2\sqrt{3}+3\right)\text{ m}\end{array} \)
20. Which of the following statements is a tautology?
\(\begin{array}{l} (\text{A})\ \left(\left(\sim p\right)\vee q \right)\Rightarrow p\end{array} \)
\(\begin{array}{l} (\text{B})\ p\Rightarrow \left(\left(\sim p\right)\vee q\right)\end{array} \)
\(\begin{array}{l} (\text{C})\ \left(\left(\sim p\right)\vee q\right)\Rightarrow q\end{array} \)
\(\begin{array}{l} (\text{D})\ q\Rightarrow \left(\left(\sim p\right)\vee q\right)\end{array} \)
Answer (D)
Sol. Truth Table
| p |
q |
~p |
~q |
(~p) ∨ q
A
B
C
D |
| ((~p) ∨ q) → p |
p → ((~p) ∨ q) |
(~p) ∨ q → q |
q → ((~p) ∨ q) |
| T |
T |
F |
F |
T |
T |
T |
T |
T |
| T |
F |
F |
T |
F |
T |
F |
T |
T |
| F |
T |
T |
F |
T |
F |
T |
T |
T |
| F |
F |
T |
T |
T |
F |
T |
F |
T |
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. Let \(\begin{array}{l} A=\begin{pmatrix}2 & -1 & -1 \\1 & 0 & -1 \\1 & -1 & 0 \\\end{pmatrix}\ \text{and}\ B = A – I.\ \text{If}\ \omega=\frac{\sqrt{3}i-1}{2},\end{array} \)
then the number of elements in the set \(\begin{array}{l} \left\{n\in\left\{1,2,\cdots,100 \right\}:A^n+\left(\omega B\right)^n=A+B \right\} \end{array} \)
is equal to _______.
Answer (17)
Sol. Here
\(\begin{array}{l} A=\begin{pmatrix}2 & -1 & -1 \\1 & 0 & -1 \\1 & -1 & 0 \\\end{pmatrix} \end{array} \)
We get A2 = A and similarly, for
\(\begin{array}{l} B=A-I=\begin{bmatrix}1 & -1 & -1 \\1 & -1 & -1 \\1 & -1 & -1 \\\end{bmatrix}\end{array} \)
We get B2 = – B⇒B3 = B
∴ An + (ωB)n = A + (ωB)n for n∈ N
For ωn to be unity n shall be multiple of 3 and for Bn to be B.n shell be 3, 5, 7, … 99
∴ n = {3, 9, 15,….. 99}
Number of elements = 17.
2. The letters of the work ‘MANKIND’ are written in all possible orders and arranged in serial order as in an English dictionary. Then the serial number of the word ‘MANKIND’ is ______.
Answer (1492)
Sol. Arranging letter in alphabetical order A D I K M N N for finding rank of MANKIND making arrangements of dictionary we get
A ………….→
\(\begin{array}{l} \frac{6!}{2!}=360\end{array} \)
D ………….→ 360
I ………….→ 360
K ………….→ 360
M A D ………….→
\(\begin{array}{l} \frac{4!}{2!}=12\end{array} \)
M A I ………….→ 12
M A K ………….→ 12
M A N D ………….→ 3! = 6
M A N I ………….→ 6
M A N K D ………….→ 2
M A N K I D ………….→ 1
M A N K I N D ………….→ 1
∴ Rank of MANKIND = 1440 + 36 + 12 + 2 + 2
= 1492
3. If the maximum value of the term independent of t in the expansion of \(\begin{array}{l} \left(t^2x^\frac{1}{5}+\frac{\left(1-x\right)^\frac{1}{10}}{t}\right),x\geq 0\end{array} \)
is K, then 8 K is equal to __________.
Answer (6006)
Sol. General Term
\(\begin{array}{l}= 15C_r\left(t^2x^\frac{1}{5}\right)^{15-r}\left(\frac{\left(1-x\right)^\frac{1}{10}}{t}\right)^r\end{array} \)
for term independent on t
2(15 – r) – r = 0
⇒ r = 10
∴ T11 = 15C10x(1 – x)
Maximum value of x (1 – x) occur at
\(\begin{array}{l} x=\frac{1}{2}\end{array} \)
\(\begin{array}{l}i.e.,\left(x(1-x)\right)_{max}=\frac{1}{4}\end{array} \)
\(\begin{array}{l}\Rightarrow K = ^{15}C_{10} \times \frac{1}{4}\end{array} \)
\(\begin{array}{l} \Rightarrow 8 K = 2(^{15}C_{10}) = 6006\end{array} \)
4. Let a, b be two non-zero real numbers. If p and r are the roots of the equation x2 – 8ax + 2a = 0 and q and s are the roots of the equation x2 + 12bx + 6b = 0, such that \(\begin{array}{l} \frac{1}{p},\frac{1}{q},\frac{1}{r},\frac{1}{s} \end{array} \)
are in A.P., then a–1 – b–1 is equal to _________.
Answer (38)
Sol. ∵ Roots of 2ax2 – 8ax + 1 = 0 are
\(\begin{array}{l} \frac{1}{p}\end{array} \)
and \(\begin{array}{l} \frac{1}{r}\end{array} \)
and roots of 6bx2 + 12bx + 1 = 0 are \(\begin{array}{l} \frac{1}{q}\end{array} \)
and \(\begin{array}{l} \frac{1}{s}\end{array} \)
.
Let
\(\begin{array}{l} \frac{1}{p},\frac{1}{q},\frac{1}{r},\frac{1}{s}\end{array} \)
as α – 3β, α – β, α + β, α + 3β
So sum of roots 2α – 2β = 4 and 2α + 2β = – 2
Clearly
\(\begin{array}{l} \alpha = \frac{1}{2} \end{array} \)
and \(\begin{array}{l} \beta =-\frac{3}{2} \end{array} \)
Now product of roots,
\(\begin{array}{l} \frac{1}{p}\cdot\frac{1}{r}=\frac{1}{2a}=-5\Rightarrow\frac{1}{a}=-10\end{array} \)
and \(\begin{array}{l} \frac{1}{q}\cdot\frac{1}{x}=\frac{1}{6a}=-8\Rightarrow\frac{1}{b}=-48\end{array} \)
So,
\(\begin{array}{l} \frac{1}{a}-\frac{1}{b}=38 \end{array} \)
5. Let a1 = b1 = 1, an = an – 1 + 2 and bn = aa + bn – 1 for every natural number n ≥ 2. Then \(\begin{array}{l} \sum_{n=1}^{15}a_n\cdot b_n\end{array} \)
is equal to ______.
Answer (27560)
Sol. a1 = b1 = 1
an = an – 1 + 2 (for n≥ 2) bn = an + bn – 1
a2 = a1 + 2 = 1 + 2 = 3 b2 = a2 + b1 = 3 + 1 = 4
a3 = a2 + 2 = 3 + 2 = 5 b3 = a3 + b2 = 5 + 4 = 9 a4 = a3 + 2 = 5 + 2 = 7 b4 = a4 + b3 = 7 + 9 = 16
a15 = a14 + 2 = 29 b15 = 225
\(\begin{array}{l} \sum_{n=1}^{15}a_n\ b_n=1\times 1+3\times 4+5\times 9+\cdots 29\times 225\end{array} \)
\(\begin{array}{l} \therefore\ \sum_{n=1}^{11}a_n\ b_n=\sum_{n=1}^{15}\left(2n-1\right)n^2=\sum_{n=1}^{15}2n^3-\sum_{n=1}^{15}n^2\end{array} \)
\(\begin{array}{l} =2\left[\frac{15\times16}{2}\right]^2-\left[\frac{15\times16\times31}{6}\right]=27560 \end{array} \)
6. Let \(\begin{array}{l} f\left(x\right)=\left\{\begin{matrix}\left|4x^2-8x+5\right|, & \text{if }8x^2-6x+1\geq 0 \\\left[4x^2-8x+5\right], & \text{if }8x^2-6x+1<0 \\\end{matrix}\right.\end{array} \)
where [α] denotes the greatest integer less than or equal to α. Then the number of points in R where f is not differentiable is
Answer (3)
Sol.
\(\begin{array}{l} f\left(x\right)=\left\{\begin{matrix}\left|4x^2-8x+5\right|, & \text{if }8x^2-6x+1\geq 0 \\\left[4x^2-8x+5\right], & \text{if }8x^2-6x+1<0 \\\end{matrix}\right.\end{array} \)
\(\begin{array}{l} =\left\{\begin{matrix}4x^2-8x+5, & \text{if }x\in \left[-\infty,\frac{1}{4}\right]\cup\left[\frac{1}{2},\infty\right) \\\left[4x^2-8x+5\right] & \text{if }x\in \left(\frac{1}{4},\frac{1}{2}\right) \\\end{matrix}\right.\end{array} \)
\(\begin{array}{l} f\left(x\right)=\left\{\begin{matrix}4x^2-8x+5 & \text{if }x\in \left(-\infty,\frac{1}{4}\right]\cup\left[\frac{1}{2},\infty\right) \\3 & x\in \left(\frac{1}{4},\frac{2-\sqrt{2}}{2}\right) \\2 & x\in\left[\frac{2-\sqrt{2}}{2},\frac{1}{2}\right) \\\end{matrix}\right.\end{array} \)
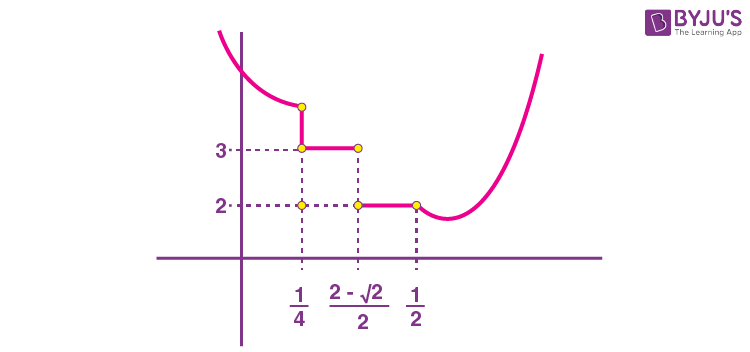
∴ Non-diff at
\(\begin{array}{l} x=\frac{1}{4},\frac{2-\sqrt{2}}{2},\frac{1}{2} \end{array} \)
7. If \(\begin{array}{l} \displaystyle \lim_{n\rightarrow\infty}\frac{\left(n+1\right)^{k-1}}{n^{k+1}}\left[\left(nk+1\right)+\left(nk+2\right)+\cdots+\left(nk+n\right)\right]\end{array} \)
\(\begin{array}{l} =33\cdot\displaystyle \lim_{n\rightarrow\infty}\frac{1}{n^{k+1}}\cdot\left[1^k+2^k+3^k+\cdots+n^k\right],\end{array} \)
then the integral value of k is equal to _______.
Answer (5)
Sol.
\(\begin{array}{l} \lim_{n\rightarrow\infty}\left(\frac{n+1}{n}\right)^{k-1}\frac{1}{n}\sum_{r=1}^{n}\left(k+\frac{r}{n}\right)=33\displaystyle \lim_{n\rightarrow\infty}\frac{1}{n}\sum_{k=1}^{n}\left(\frac{r}{n}\right)^k\end{array} \)
\(\begin{array}{l} \Rightarrow \int_0^1\left(k+x\right)dx=33\int_0^1x^kdx\end{array} \)
8. Let the equation of two diameters of a circle x2 + y2 – 2x + 2fy + 1 = 0 be 2px – y = 1 and 2x + py = 4p. Then the slope m ∈ (0, ∞) of the tangent to the hyperbola 3x2 – y2 = 3 passing through the centre of the circle is equal to _______.
Answer (2)
Sol. x2 + y2 – 2x + 2fy + 1 = 0 [entre = (1, –f]
Diameter 2px – y = 1 …(i)
2x + py = 4p …(ii)
\(\begin{array}{l} x=\frac{5P}{2P^2+2} \end{array} \)
\(\begin{array}{l} y=\frac{4P^2-1}{1+P^2} \end{array} \)
\(\begin{array}{l} \because x=1\end{array} \)
f = 0 \(\begin{array}{l}[\text{for}\ P=\frac{1}{2}]\end{array} \)
\(\begin{array}{l} \frac{5P}{2P^2+2}=1 \end{array} \)
f = 3 [for P = 2]
\(\begin{array}{l} \therefore P=\frac{1}{2},2\end{array} \)
\(\begin{array}{l}\text{Centre can be} \left(\frac{1}{2},0\right)\text{ or }\left(1,3\right)\end{array} \)
\(\begin{array}{l} \left(\frac{1}{2},0\right)\text{will not satisfy}\end{array} \)
∴ Tangent should pass through (2, 3) for 3x2 – y2 = 3
\(\begin{array}{l} \frac{x^2}{1}-\frac{y^2}{3}=1 \end{array} \)
\(\begin{array}{l} y=mx\pm\sqrt{m^2-3}\end{array} \)
Substitute (2, 3)
\(\begin{array}{l} 3=m\pm\sqrt{m^2-3}\end{array} \)
\(\begin{array}{l} \therefore\ m=2\end{array} \)
9. The sum of diameters of the circles that touch (i) the parabola 75x2 = 64(5y – 3) at the point (8/5, 6/5) and (ii) the y-axis is equal to _______.
Answer (10)
Sol.
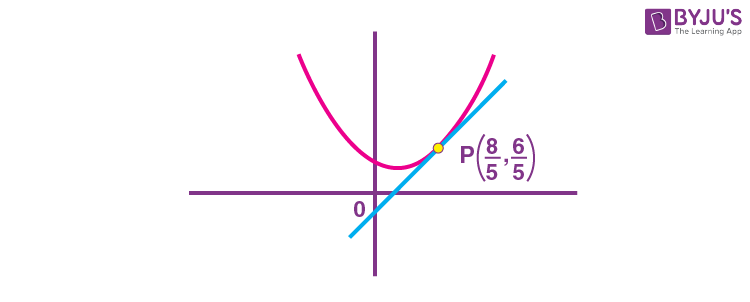
Equation of tangent to the parabola at
\(\begin{array}{l} P\left(\frac{8}{5},\frac{6}{5}\right) \end{array} \)
\(\begin{array}{l} 75x\cdot\frac{8}{5}=160\left(y+\frac{6}{5}\right)-192\end{array} \)
⇒ 120x = 160y
⇒ 3x = 4y
Equation of circle touching the given parabola at P can be taken as
\(\begin{array}{l} \left(x-\frac{8}{5}\right)^2+\left(y-\frac{6}{5}\right)^2+\lambda\left(3x-4y\right)=0\end{array} \)
If this circle touches y-axis then
\(\begin{array}{l} \frac{64}{25}+\left(y-\frac{6}{5}\right)^2+\lambda\left(-4y\right)=0 \end{array} \)
\(\begin{array}{l} \Rightarrow y^2-2y\left(2\lambda+\frac{6}{5}\right)+4=0\end{array} \)
⇒ D = 0
\(\begin{array}{l} \Rightarrow \left(2\lambda+\frac{6}{6}\right)^2=4\end{array} \)
\(\begin{array}{l} \Rightarrow \lambda=\frac{2}{5}\text{ or }-\frac{8}{5}\end{array} \)
Radius = 1 or 4
Sum of diameter = 10
10. The line of shortest distance between the lines \(\begin{array}{l} \frac{x-2}{0}=\frac{y-1}{1}=\frac{z}{1}\ \text{and}\ \frac{x-3}{2}=\frac{y-5}{2}=\frac{z-1}{1}\end{array} \)
makes an angle of \(\begin{array}{l} \cos^{-1}\left(\sqrt{\frac{2}{27}}\right) \end{array} \)
with the plane P : ax – y – z = 0, (a> 0). If the image of the point (1, 1, –5) in the plane P is (α, β, γ), then α + β – γ is equal to ________.
Answer (*)
Sol.
\(\begin{array}{l}\text{Line of shortest distance will be along }\overline{b_1}\times \overline{b_2}\end{array} \)
Where,
\(\begin{array}{l}\overline{b_1}=\hat{j}+\hat{k}\end{array} \)
and \(\begin{array}{l} \overrightarrow{b_2}=2\hat{i}+2\hat{j}+\hat{k} \end{array} \)
\(\begin{array}{l} \overline{b_1}\times\overline{b_2}=\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\ 0& 1 & 1 \\2 & 2 & 1 \\\end{vmatrix}=-\hat{i}+2\hat{j}-2\hat{k}\end{array} \)
\(\begin{array}{l}\text{Angle between}\ \overline{b_1}\times\overline{b_2} \text{ and plane P},\end{array} \)
\(\begin{array}{l} \sin\theta=\left|\frac{-a-2+2}{3\cdot\sqrt{a^2+2}}\right|=\frac{5}{\sqrt{27}}\Rightarrow \frac{\left|a \right|}{\sqrt{a^2+2}}=\frac{5}{\sqrt{3}}\end{array} \)
\(\begin{array}{l} \Rightarrow\ a^2=-\frac{25}{11} \left(\text{not possible}\right)\end{array} \)
JEE Main 2022 July 25th Shift 1 Paper Analysis





















Comments