The JEE Main 2022 July 27 β Shift 1 Maths Question Paper with Solutions will be available on this page. JEE Main 2022 answer keys are created by subject experts at BYJUβS. Students can use the JEE Main 2022 question papers to understand the difficulty level and exam pattern. It will also help them to check the correct answers and thus analyse their performance. Practising these solutions will help students to improve their confidence and problem-solving skills.
JEE Main 2022 27th July Shift 1 Mathematics Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. Let R1 and R2 be two relations defined on β by a R1b β ab β₯ 0 and aR2b β a β₯ b. Then,
(A) R1 is an equivalence relation but not R2
(B) R2 is an equivalence relation but not R1
(C) Both R1 and R2 are equivalence relations
(D) Neither R1 nor R2 is an equivalence relation
Answer (D)
Sol. a R1b β ab β₯ 0
So, definitely (a, a) β R1 as a2 β₯ 0
If (a, b) β R1 β (b, a) β R1
But if (a, b) β R1, (b, c) β R1
β Then (a, c) may or may not belong to R1
{Consider a = β5, b = 0, c = 5 so (a, b) and (b, c) β R1 but ac < 0}
So, R1 is not equivalence relation
a R2 b β a β₯ b
(a, a) β R2 β so reflexive relation
If (a, b) β R2 then (b, a) may or may not belong to R2
β So not symmetric
Hence it is not equivalence relation
2. Let \(\begin{array}{l}f,g : \mathbb{N} = \{1\} \rightarrow \mathbb{N}\ \text{be functions defined by}\end{array} \)
f(a) = Ξ±, where Ξ± is the maximum of the powers of those primes p such that pΞ± divides a, and g(a) = a + 1, for all a β N – {1}. Then, the functionΒ f + g is
(A) One-one but not onto
(B) Onto but not one-one
(C) Both one-one and onto
(D) Neither one-one nor onto
Answer (D)
Sol. f, g : N β {1} β N defined as
f(a) = Ξ±, where Ξ± is the maximum power of those primes p such that pΞ± divides a.
g(a) = a + 1,
Now, f(2) = 1, g(2) = 3 β (f + g) (2) = 4
f(3) = 1, g(3) = 4 β (f + g) (3) = 5
f(4) = 2, g(4) = 5 β (f + g) (4) = 7
f(5) = 1, g(5) = 6 β (f + g) (5) = 7
β΅ (f + g) (5) = (f + g) (4)
β΄ f + g is not one-one
Now, β΅ fmin = 1, gmin = 3
So, there does not exist any x β N β {1} such that
(f + g)(x) = 1, 2, 3
β΄ f + g is not onto
3. Let the minimum value v0 of \(\begin{array}{l}v= \left|z\right|^2 + \left|z – 3\right|^2 + \left|z – 6i\right|^2, z \in \mathbb {C}\end{array} \)
is attained at z = z0. Then \(\begin{array}{l}\left|2z_0^2 – \bar{z}_0^3 + 3 \right|^2 + v_0^2\end{array} \)
is equal to
(A) 1000
(B) 1024
(C) 1105
(D) 1196
Answer (A)
Sol. Let z = x + iy
v = x2 + y2 + (x β 3)2 + y2 + x2 + (y β 6)2
= (3x2 β 6x + 9) + (3y2 β 12y + 36)
= 3(x2 + y2 β 2x β 4y + 15)
= 3[(x β 1)2 + (y β 2)2 + 10]
vmin at z = 1 + 2i = z0 and v0 = 30
so |2(1 + 2i)2 β (1 β 2i)3 + 3|2 + 900
= |2(β3 + 4i) β (1 β 8i3 β 6i (1 β 2i) +3|2 + 900
= |β6 + 8i β (1 + 8i β 6i β 12) + 3|2 + 900
= |8 + 6i|2 + 900
= 1000
4. Let \(\begin{array}{l}A = \begin{pmatrix}1 & 2 \\-2 & -5 \\\end{pmatrix}\end{array} \)
. Let Ξ±, Ξ² β β be such that Ξ±A2 + Ξ²A = 2I. Then Ξ± + Ξ² is equal to
(A) β10
(B) β6
(C) 6
(D) 10
Answer (D)
Sol.
\(\begin{array}{l}A^2 = \begin{bmatrix}1 & 2 \\-2 & -5 \\\end{bmatrix}\begin{bmatrix}1 & 2 \\-2 & -5 \\\end{bmatrix} = \begin{bmatrix}-3 & -8 \\8 & 21 \\\end{bmatrix} \end{array} \)
\(\begin{array}{l}\alpha A^2 + \beta A = \begin{bmatrix}-3\alpha & -8\alpha \\8\alpha & 21\alpha \\\end{bmatrix} +\begin{bmatrix}\beta & 2\beta \\-2\beta & -5\beta \\\end{bmatrix} \end{array} \)
\(\begin{array}{l}= \begin{bmatrix}-3\alpha + \beta & -8\alpha + 2 \beta \\8\alpha – 2\beta & 21\alpha – 5\beta \\\end{bmatrix} = \begin{bmatrix}2 & 0 \\0 & 2 \\\end{bmatrix}\end{array} \)
On Comparing
\(\begin{array}{l}8 \alpha = 2 \beta, -3 \alpha + \beta = 2, 21\alpha – 5\beta = 2\\ \Rightarrow \alpha = 2, \beta = 8\end{array} \)
So, Ξ± + Ξ² = 10
5. The remainder when (2021)2022 + (2022)2021 is divided by 7 is
(A) 0
(B) 1
(C) 2
(D) 6
Answer (A)
Sol.
\(\begin{array}{l}\left(2021\right)^{2022} + \left (2022\right )^{2021}\\ = \left (7k – 2\right )^{2022} + \left(7k_1 – 1\right)^{2021}\end{array} \)
\(\begin{array}{l}=[(7k – 2)^3]^{674}+ (7k_1)^{2021}-2021(7k_1)^{2020}+…-1\end{array} \)
\(\begin{array}{l}= \left (7k_2 – 1\right )^{674} + \left (7m – 1\right) = \left (7n + 1\right) + \left(7m – 1\right) = 7\left(m + n\right) \left(\text{multiple of}~7\right)\\ \therefore \text{Remainder =} 0\end{array} \)
6. Suppose a1, a2, β¦ an, β¦ be an arithmetic progression of natural numbers. If the ration of the sum of first five terms to the sum of first nine terms of the progression is 5 : 17 and 110 < a15 < 120, then the sum of the first ten terms of the progression is equal to
(A) 290
(B) 380
(C) 460
(D) 510
Answer (B)
Sol. β΅ a1, a2, β¦ an β¦ be an A.P of natural numbers and
\(\begin{array}{l}\frac{S_5}{S_9}=\frac{5}{17}\Rightarrow \frac{\frac{5}{2}[2a_1 + 4d]}{\frac{9}{2}[2a_1 + 8d]}=\frac{5}{17}\end{array} \)
\(\begin{array}{l}\Rightarrow 34a_1 + 68d = 18a_1 + 72d\\ \Rightarrow 16a_1 = 4d\\ \therefore d = 4a_1 \end{array} \)
\(\begin{array}{l}\text{And}~ 110 < a_{15} <120\\ \therefore 110 < a_1 + 14d < 120 \\ \Rightarrow 110 < 57a_1 < 120\end{array} \)
\(\begin{array}{l} \therefore a_1 = 2 (\because a_i \in N)\\ d = 8\\ \therefore S_{10} = 5 \left[4 + 9 \times 8\right] = 380\end{array} \)
7. Let β β β be function defined as \(\begin{array}{l}f(x)=a\sin \left(\frac{\pi [x]}{2}\right) + [2-x], a\in \mathbb{R}\end{array} \)
where [t] is the greatest integer less than or equal to t. \(\begin{array}{l}\text{If}\ \displaystyle \lim_{ x \to 1}f(x)\ \text{exists, then the value of}\ \int_{0}^{4}f(x) dx\end{array} \)
is equal to
(A) β1
(B) β2
(C) 1
(D) 2
Answer (B)
Sol. \(\begin{array}{l}f(x)=a\sin\left(\frac{\pi[x]}{2}\right) + [2-x] \ a \in R\end{array} \)
Now,
\(\begin{array}{l}\because \displaystyle \lim_{x \to -1}f(x) \text{ exists}\end{array} \)
\(\begin{array}{l}\therefore \displaystyle \lim_{x \to -1^-}f(x) = \displaystyle \lim_{x \to -1^+}f(x)\end{array} \)
\(\begin{array}{l}\Rightarrow a\sin\left( \frac{-2\pi}{2}\right)+3 = a \sin \left(\frac{-\pi}{2}\right)+2\end{array} \)
\(\begin{array}{l}\Rightarrow -a =1 \Rightarrow a = -1\end{array} \)
\(\begin{array}{l}\text{Now, } \int_{0}^{4}f(x)dx = \int_{0}^{4}\left(-\sin \left(\frac{\pi[x]}{2} \right) + [2-x]\right)dx\end{array} \)
\(\begin{array}{l}=\int_{0}^{1}1dx + \int_{1}^{2}-1dx + \int_{2}^{3}-1dx + \int_{3}^{4}(1-2)dx \\= 1 – 1 – 1 – 1 = – 2\end{array} \)
8. Let \(\begin{array}{l}I = \int_{\pi / 4}^{\pi /3}\left( \frac{8\sin x – \sin 2x}{x} \right)dx\end{array} \)
Then
\(\begin{array}{l}(\text{A})\ \frac{\pi}{2}<I<\frac{3\pi}{4}\end{array} \)
\(\begin{array}{l}(\text{B})\frac{\pi}{5}<I<\frac{5\pi}{12}\end{array} \)
\(\begin{array}{l}(\text{C})\ \frac{5\pi}{12}<I<\frac{\sqrt{2}}{3}\pi\end{array} \)
\(\begin{array}{l}(\text{D})\ \frac{3\pi}{4}<I<\pi\end{array} \)
Answer (*)
Sol. I comes out around 1.536 which is not satisfied by any given options.
\(\begin{array}{l}\int_{\pi/4}^{\pi/3}\frac{8x-2x}{x}dx > I > \int_{\pi/4}^{\pi/3}\frac{8\sin x – 2x}{x}dx\end{array} \)
\(\begin{array}{l}\frac{\pi}{2}> I > \int_{\pi/4}^{\pi/3}\left(\frac{8\sin x}{x}-2\right)dx\end{array} \)
\(\begin{array}{l}\frac{\sin x}{x}\ \text{is decreasing in}\ \left( \frac{\pi}{4}, \frac{\pi}{3}\right)\end{array} \)
so it attains maximum at
\(\begin{array}{l}x = \frac{x}{4}\end{array} \)
\(\begin{array}{l}I > \int_{\pi/4}^{\pi/3}\left(\frac{8\sin \pi /3}{\pi /3} – 2\right)dx\end{array} \)
\(\begin{array}{l}I > \sqrt{3}-\frac{\pi}{6}\end{array} \)
9. The area of the smaller region enclosed by the curves y2 = 8x + 4 and \(\begin{array}{l}x^2 +y^2 + 4\sqrt{3}x-4 =0\end{array} \)
is equal to
\(\begin{array}{l}(\text{A})\ \frac{1}{3}(2-12\sqrt{3} + 8\pi)\end{array} \)
\(\begin{array}{l}(\text{B})\ \frac{1}{3}(2-12\sqrt{3} + 6\pi)\end{array} \)
\(\begin{array}{l}(\text{C})\ \frac{1}{3}(4-12\sqrt{3} + 8\pi)\end{array} \)
\(\begin{array}{l}(\text{D})\ \frac{1}{3}(4-12\sqrt{3} + 6\pi)\end{array} \)
Answer (C)
Sol.
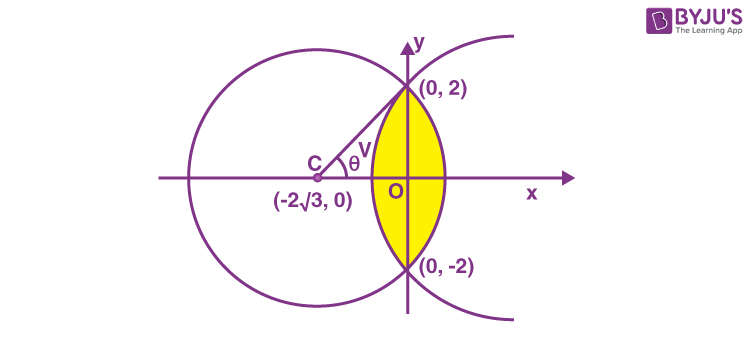
\(\begin{array}{l}\cos \theta = \frac{2\sqrt{3}}{4}=\frac{\sqrt{3}}{2} \Rightarrow \theta = 30^{\circ}\end{array} \)
Area of the required region
\(\begin{array}{l}=\frac{2}{3}\left(4 \times \frac{1}{2}\right)+4^2 \times \frac{\pi}{6}-\frac{1}{2}\times 4 \times 2 \sqrt{3}\end{array} \)
\(\begin{array}{l}=\frac{4}{3}+\frac{8\pi}{3}-4\sqrt{3}=\frac{1}{3}\{{4-12\sqrt{3}+ 8\pi}\}\end{array} \)
10. Let y = y1(x) and y = y2(x) be two distinct solution of the differential equation \(\begin{array}{l}\frac{dy}{dx}=x+y,\end{array} \)
with y1(0) = 0 and y2(0) = 1 respectively. Then, the number of points of intersection of y = y1 (x) and y = y2(x) is
(A) 0
(B) 1
(C) 2
(D) 3
Answer (A)
Sol.
\(\begin{array}{l}\frac{dy}{dx}=x+y\end{array} \)
Let x + y = t
\(\begin{array}{l}1 + \frac{dy}{dx}=\frac{dt}{dx}\end{array} \)
\(\begin{array}{l}\frac{dt}{dx}-1 =t\Rightarrow \int\frac{dt}{t + 1} =\int dx\end{array} \)
\(\begin{array}{l}\ln |t+1| = x + C'\end{array} \)
\(\begin{array}{l}|t+1| = Ce^x\end{array} \)
\(\begin{array}{l}|x+y + 1| = Ce^x\end{array} \)
\(\begin{array}{l}\text{For}~ y_1\left(x\right), y_1\left(0\right) = 0 \Rightarrow C = 1\\ \text{For}~ y_2\left(x\right), y_2\left(0\right) = 1 \Rightarrow C = 2\end{array} \)
\(\begin{array}{l} y_1\left(x\right)\text{is given by} \left|x + y + 1\right| = e^x\\ y_2\left(x\right)\text{is given by} \left|x + y + 1\right| = 2e^x \end{array} \)
At point of intersection
\(\begin{array}{l} e^x = 2e^x \end{array} \)
No solution
So, there is no point of intersection of y1(x) and y2(x).
11. Let P(a, b) be a point on the parabola y2 = 8x such that the tangent at P passes through the centre of the circle x2 + y2 β 10x β 14y + 65 = 0. Let A be the product of all possible values of a and B be the product of all possible values of b. Then the value of A + B is equal to
(A) 0
(B) 25
(C) 40
(D) 65
Answer (D)
Sol. Centre of circle x2 + y2 β 10x β14y + 65 = 0 is at (5, 7).
Let the equation of tangent to y2 = 8x is
yt = x + 2t2
which passes through (5, 7)
7t = 5 + 2t2
β 2t2 β 7t + 5 = 0
\(\begin{array}{l}t = 1, \frac{5}{2}\end{array} \)
\(\begin{array}{l}A = 2 \times 1^2 \times 2 \times \left( \frac{5}{2}\right)^2 = 25\end{array} \)
\(\begin{array}{l}B = 2 \times 2 \times 1 \times 2 \times 2 \times \frac{5}{2} = 40\\A + B = 65\end{array} \)
12. \(\begin{array}{l}\text{Let}~\vec{a} = \alpha \hat{i} + \hat{j} + \beta \hat{k}~\text{and}~ \vec{b} = 3 \hat{i} + 5\hat{j} + 4 \hat{k}~ \text{be two vectors, such that }\vec{a} \times \vec{b} = -\hat{i} + 9\hat{j} + 12 \hat{k}.~\text{Then the projection of } \vec{b}-2\vec{a} ~\text{on}~ \vec{b}+ \vec{a}~\text {is equal to}\end{array} \)
\(\begin{array}{l}(\text{A})\ 2\end{array} \)
\(\begin{array}{l}(\text{B})\ \frac{39}{5}\end{array} \)
\(\begin{array}{l}(\text{C})\ 9\end{array} \)
\(\begin{array}{l}(\text{D})\ \frac{46}{5}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}\vec{a}=\alpha \hat{i} + \hat{j}+ \beta \hat{k}, \vec{b} = 3\hat{i} – 5\hat{j}+ 4 \hat{k}\end{array} \)
\(\begin{array}{l}\vec{a}\times \vec{b} = -\hat{i} + 9\hat{j}+ 12 \hat{k}\end{array} \)
\(\begin{array}{l}\begin{vmatrix}\hat{i} & \hat{j} & \hat{k} \\\alpha & 1 & \beta \\3 & -5 & 4 \\\end{vmatrix}=-\hat{i}+9\hat{j}+12\hat{k}\end{array} \)
\(\begin{array}{l}4 + 5\beta = -1 \Rightarrow \beta = -1\\ -5\alpha – 3 = 12 \Rightarrow \alpha = -3\end{array} \)
\(\begin{array}{l}\vec{b}-2\vec{a}=3\hat{i}-5\hat{j}+4\hat{k}-2(-3\hat{i} + \hat{j}-\hat{k})\end{array} \)
\(\begin{array}{l}\vec{b}-2\vec{a}=9\hat{i}-7\hat{j}+6\hat{k}\end{array} \)
\(\begin{array}{l}\vec{b}+ \vec{a}=(3\hat{i}-5\hat{j}+4\hat{k}) + (-3\hat{i}+\hat{j}-\hat{k})\end{array} \)
\(\begin{array}{l}\vec{b}+ \vec{a}=-4\hat{j}+3\hat{k} \end{array} \)
\(\begin{array}{l}\text{Projection of }\vec{b}- 2\vec{a} \text{ on } \vec{b} + \vec{a} = \frac{(\vec{b}-2\vec{a})\cdot(\vec{b} + \vec{a})}{|\vec{b} + \vec{a}|}\end{array} \)
\(\begin{array}{l}=\frac{28+18}{5}=\frac{46}{5}\end{array} \)
13. \(\begin{array}{l}\text{Let}~\vec{a} = 2\hat{i}-\hat{j}+5\hat{k}~\text{and}~ \vec{b} = \alpha \hat{i} + \beta \hat{j}+2\hat{k}. \text{If}~((\vec{a}\times \vec{b}) \times \hat{i})\cdot \hat{k}=\frac{23}{2},~ \text{then} \left|\vec{b}\times 2\hat{j}\right| \text{is equal to} \end{array} \)
\(\begin{array}{l}(\text{A})\ 4\end{array} \)
\(\begin{array}{l}(\text{B})\ 5\end{array} \)
\(\begin{array}{l}(\text{C})\ \sqrt{21}\end{array} \)
\(\begin{array}{l}(\text{D})\ \sqrt{17}\end{array} \)
Answer (B)
Sol. Given,
\(\begin{array}{l}\vec{a}=2\hat{j}-\hat{j}+5\hat{k}\end{array} \)
and \(\begin{array}{l}\vec{b}=\alpha\hat{j}+ \beta \hat{j}+2\hat{k}\end{array} \)
Also,
\(\begin{array}{l}((\vec{a} \times \vec{b} )\times i)\cdot \hat{k} = \frac{23}{2}\end{array} \)
\(\begin{array}{l}\Rightarrow ((\vec{a}\cdot \hat{i})\vec{b}-(\vec{b}\cdot\hat{i})\cdot \vec{a})\cdot \hat{k}=\frac{23}{2}\end{array} \)
\(\begin{array}{l}\Rightarrow (2\cdot \vec{b}- \alpha \cdot\vec{a})\cdot\hat{k}=\frac{23}{2}\end{array} \)
\(\begin{array}{l}\Rightarrow 2 \cdot 2 – 5\alpha= \frac{23}{2}\Rightarrow \alpha = \frac{-3}{2}\end{array} \)
\(\begin{array}{l}\text{Now, } |\vec{b}\times 2\hat{j}|=|(\alpha \hat{i} + \beta \hat{j} + 2 \hat{k}) \times 2 \hat{j}|\end{array} \)
\(\begin{array}{l}=|2\alpha \hat{k}+ 0 – 4\hat{i}|\end{array} \)
\(\begin{array}{l}=\sqrt{4\alpha^2 + 16}\end{array} \)
\(\begin{array}{l}=\sqrt{4\left(\frac{-3}{2} \right)^2 + 16}= 5\end{array} \)
14. Let S be the sample space of all five digit numbers. It p is the probability that a randomly selected number from S, is multiple of 7 but not divisible by 5, then 9p is equal to
(A) 1.0146
(B) 1.2085
(C) 1.0285
(D) 1.1521
Answer (C)
Sol. Among the 5 digit numbers,
First number divisible by 7 is 10003 and last is 99995.
\(\begin{array}{l}\Rightarrow \text{Number of numbers divisible by 7.}\\ =\frac{99995-10003}{7}+1 = 12857 \end{array} \)
First number divisible by 35 is 10010 and last is 99995.
\(\begin{array}{l}\Rightarrow \text{Number of numbers divisible by 35} = \frac{99995-10010}{35}+1= 2572 \end{array} \)
Hence number of number divisible by 7 but not by 5
= 12857 β 2572
= 10285
\(\begin{array}{l}9P = \frac{10285}{90000}\times 9\end{array} \)
= 1.0285
15. Let a vertical tower AB of height 2h stands on a horizontal ground. Let from a point P on the ground a man can see upto height h of the tower with an angle of elevation 2Ξ±. Β \(\begin{array}{l}\text{When from P, he moves a distance d in the direction of}\ \overrightarrow{AP},\end{array} \)
he can see the top B of the tower with an angle of elevation Ξ±. if d = β7 h, then tan Ξ± is equal to
\(\begin{array}{l}(\text{A})\ \sqrt{5}-2\end{array} \)
\(\begin{array}{l}(\text{B})\ \sqrt{3}-1\end{array} \)
\(\begin{array}{l}(\text{C})\ \sqrt{7}-2\end{array} \)
\(\begin{array}{l}(\text{D})\ \sqrt{7}-\sqrt{3}\end{array} \)
Answer (C)
Sol.
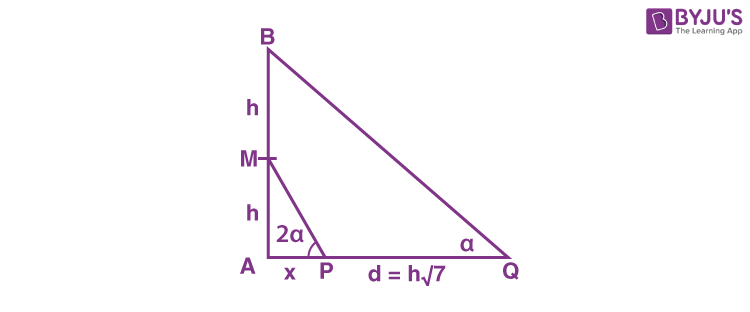
\(\begin{array}{l}\triangle APM \text{gives} \tan 2\alpha = \frac{h}{x}~~~~~~~~…(i)\end{array} \)
\(\begin{array}{l}\triangle AQB ~\text{gives} \tan \alpha = \frac{2h}{x+ d} = \frac{2h}{x+h\sqrt{7}}~~~~~~~~…(ii)\end{array} \)
From (i) and (ii)
\(\begin{array}{l}\tan \alpha = \frac{2\cdot \tan 2\alpha}{1 + \sqrt{7}\cdot \tan 2\alpha}\end{array} \)
Let t = tan Ξ±
\(\begin{array}{l}\Rightarrow t = \frac{2\frac{2t}{1-t^2}}{1+\sqrt{7}\cdot \frac{2t}{1-t^2}}\end{array} \)
\(\begin{array}{l}\Rightarrow t^2 – 2\sqrt{7}t + 3 =0\end{array} \)
\(\begin{array}{l} t= \sqrt{7} -2\end{array} \)
16. \(\begin{array}{l}(p \land r )\Leftrightarrow ( p \land (\sim q))\end{array} \)
is equivalent to (~ p) when r is
(A) p
(B) ~p
(C) q
(D) ~q
Answer (C)
Sol. The truth table
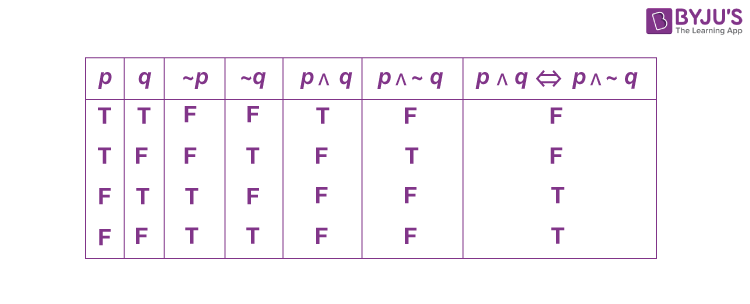
\(\begin{array}{l}\text{Clearly} p \wedge q \Leftrightarrow p \wedge \sim q \equiv \sim p \\\therefore r = q\end{array} \)
17. If the plane P passes through the intersection of two mutually perpendicular planes 2x + ky β 5z = 1 and 3kx β ky + z = 5, k < 3 and intercepts a unit length on positive x-axis, then the intercept made by the plane P on the y-axis is
\(\begin{array}{l}(\text{A}) \ \frac{1}{11} \end{array} \)
\(\begin{array}{l}(\text{B}) \ \frac{5}{11} \end{array} \)
\(\begin{array}{l}(\text{C}) \ 6\end{array} \)
\(\begin{array}{l}(\text{D}) \ 7 \end{array} \)
Answer (D)
Sol. P1 : 2x + ky β 5z = 1
P2 : 3kx β ky + z = 5
\(\begin{array}{l}\because P_1 \perp P_2 \Rightarrow 6k-k^2+5 = 0 \end{array} \)
\(\begin{array}{l}\Rightarrow k = 1, 5 \because k < 3 \therefore k = 1\end{array} \)
\(\begin{array}{l}P_1 : 2x + y – 5z = 1 \end{array} \)
\(\begin{array}{l}P_2 : 3x – y + z = 5 \end{array} \)
\(\begin{array}{l}P: (2x+y-5z -1) + \lambda(3x -y + z -5)=0 \end{array} \)
\(\begin{array}{l}\text{Positive x-axis intercept =} 1\Rightarrow \frac{1+5\lambda}{2+3\lambda}=1\end{array} \)
\(\begin{array}{l}\Rightarrow \lambda = \frac{1}{2}\end{array} \)
\(\begin{array}{l}\because P \colon 7x + y – 4z = 7 \\ \text{y intercept =} 7. \end{array} \)
18. Let A(1, 1), B(-4, 3) and C(-2, -5) be vertices of a triangle ABC, P be a point on side BC, and Ξ1 and Ξ2 be the areas of triangles APB and ABC, respectively. If Ξ1 : Ξ2 = 4 : 7, then the area enclosed by the lines AP, AC and the x-axis is
\(\begin{array}{l}(\text{A})\ \frac{1}{4}\end{array} \)
\(\begin{array}{l}(\text{B})\ \frac{3}{4}\end{array} \)
\(\begin{array}{l}(\text{C})\ \frac{1}{2}\end{array} \)
\(\begin{array}{l}(\text{D})\ 1\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}\frac{\Delta_1}{\Delta_2}=\frac{\frac{1}{2} \times BP \times AH}{\frac{1}{2} \times BC \times AH} = \frac{4}{7}\end{array} \)
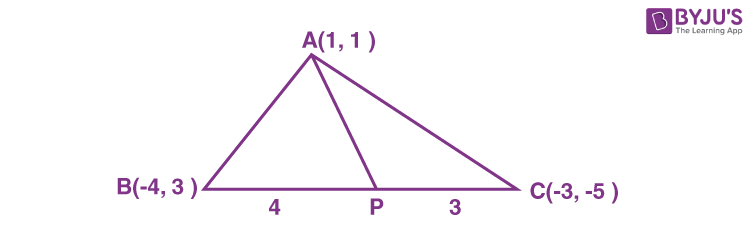
\(\begin{array}{l}P\left(\frac{-20}{7}, \frac{-11}{7}\right)\end{array} \)
Line AC : y β 1 = 2(x β 1)
Intersection with x-axis
\(\begin{array}{l}=\left(\frac{1}{2},0\right)\end{array} \)
\(\begin{array}{l}\text{Line }AP: y-1 = \frac{2}{3}(x-1)\end{array} \)
Intersection with x-axis
\(\begin{array}{l}\left(\frac{-1}{2},0\right)\end{array} \)
\(\begin{array}{l}\text{ Vertices are }(1,1), \left(\frac{1}{2},0\right) \text{ and } \left(\frac{-1}{2},0\right)\end{array} \)
\(\begin{array}{l}\text{Area } = \frac{1}{2} \text{ sq. unit}\end{array} \)
19. If the circle \(\begin{array}{l}x^2 + y^2 – 2gx + 6y – 19c = 0, g, c \in \mathbb {R} \end{array} \)
passes through the point (6, 1) and its centre lies on the line x β 2cy = 8, then the length of intercept made by the circle on x-axis is
\(\begin{array}{l}(\text{A})\ \sqrt{11}\end{array} \)
\(\begin{array}{l}(\text{B})\ 4\end{array} \)
\(\begin{array}{l}(\text{C})\ 3 \end{array} \)
\(\begin{array}{l}(\text{D})\ 2\sqrt{23}\end{array} \)
Answer (D)
Sol. Circle : x2 + y2 β 2gx + 6y β 19c = 0
It passes through h(6, 1)
β 36 + 1 β 12g + 6 β 19c = 0
= 12g + 19c = 43 β¦(1)
Line x β 2cy = 8 passes though centre
β g + 6c = 8 β¦(2)
From (1) & (2)
g = 2, c = 1
C : x2 + y2 β 4x + 6y β 19 = 0
\(\begin{array}{l}x \text{\ int }=2\sqrt{g^2-C} \end{array} \)
\(\begin{array}{l}=2\sqrt{4+19}\end{array} \)
\(\begin{array}{l}=2\sqrt{23}\end{array} \)
20. Let a function f: β β β be defined as :
\(\begin{array}{l}f(x) = \left\{\begin{matrix}\int_{0}^{x}(5-|t-3|)dt, & x>4 \\x^2 + bx, & x \le4 \\\end{matrix}\right.\end{array} \)
where b β β. If f is continuous at x = 4 then which of the following statements is NOT true?
\(\begin{array}{l}(\text{A})\ \text{f is not differentiable at x} = 4 \end{array} \)
\(\begin{array}{l}(\text{B})\ f'(3)+f'(5)=\frac{35}{4}\end{array} \)
\(\begin{array}{l}(\text{C})\ f \text{ is increasing in } \left(-\infty, \frac{1}{8}\right) \cup (8, \infty)\end{array} \)
\(\begin{array}{l}(\text{D})\ f \text{ has a local minima at } x = \frac{1}{8}\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}\because f(x) \text{is continuous at }x = 4 \Rightarrow f\left(4^-\right) = f\left(4^+\right)\end{array} \)
\(\begin{array}{l}\Rightarrow 16 + 4b = \int_{0}^{4}(5-|t-3|)dt\end{array} \)
\(\begin{array}{l}=\int_{0}^{3}(2+t)dt+\int_{3}^{4}(8-t)dt\end{array} \)
\(\begin{array}{l}=2t +\left. \frac{t^2}{2}\right)_0^3+8t – \left. \frac{t^2}{3}\right]_{3}^4\end{array} \)
\(\begin{array}{l}=6+\frac{9}{2}-0 + (32-8)-\left(24-\frac{9}{2}\right)\end{array} \)
16 + 4b = 15
\(\begin{array}{l}\Rightarrow b = \frac{-1}{4}\end{array} \)
\(\begin{array}{l}\Rightarrow f(x) = \left\{\begin{matrix}\int_{0}^{x}5-|t-3|dt & x>4 \\x^2-\frac{x}{4} & x\le 4 \\\end{matrix}\right.\end{array} \)
\(\begin{array}{l}\Rightarrow f'(x) = \left\{\begin{matrix}5-|x-3| & x>4 \\2x-\frac{1}{4} & x\le 4 \\\end{matrix}\right.\end{array} \)
\(\begin{array}{l}\Rightarrow f'(x) = \left\{\begin{matrix}8-x & x>4 \\2x-\frac{1}{4} & x\le 4 \\\end{matrix}\right.\end{array} \)
\(\begin{array}{l}f'(x)<0 \Rightarrow x \in \left(-\infty, \frac{1}{8}\right)\cup (8, \infty)\end{array} \)
\(\begin{array}{l}f'(3)+f'(5)=6 -\frac{1}{4}=\frac{35}{4}\end{array} \)
\(\begin{array}{l}f'(x) = 0 \Rightarrow x = \frac{1}{8} \text{ have local minima}\end{array} \)
\(\begin{array}{l}\therefore \left(C\right) \text{is only incorrect option}\end{array} \)
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, β00.33, β00.30, 30.27, β27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. For k β R, let the solution of the equation
\(\begin{array}{l}\cos(\sin^{-1}(x\cot (\tan^{-1}(\cos (\sin^{-1})))))= k,0 < |x|<\frac{1}{\sqrt{2}}\end{array} \)
Inverse trigonometric functions take only principal values. If the solutions of the equation x2 β bx β 5 = 0 are \(\begin{array}{l}\frac{1}{\alpha^2} + \frac{1}{\beta^2} \text{ and }\frac{\alpha}{\beta}\end{array} \)
, then b/k2 is equal to ______.
Answer (12)
Sol.
\(\begin{array}{l}\cos(\sin^{-1}(x\cot (\tan^{-1}(\cos (\sin^{-1})))))= k\end{array} \)
\(\begin{array}{l}\Rightarrow \cos(\sin^{-1}(x\cot (\tan^{-1} \sqrt{1-x^2})))= k\end{array} \)
\(\begin{array}{l}\Rightarrow \cos \left( \sin^{-1} \left( \frac{x}{\sqrt{1-x^2}}\right)\right) = k\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{\sqrt{1-2x^2}}{\sqrt{1-x^2}}=k\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{1-2x^2}{1-x^2}=k^2\end{array} \)
\(\begin{array}{l}\Rightarrow 1 – 2x^2 = k^2 – k^2x^2\end{array} \)
β΄ Ξ±, Ξ² be the roots of x2 – (k2 – 1)/(k2 – 2) = 0
\(\begin{array}{l}\frac{1}{\alpha^2}+\frac{1}{\beta^2}=2\left(\frac{k^2-2}{k^2-1}\right)~~~~~~…(1)\end{array} \)
\(\begin{array}{l}\text{and } \frac{\alpha}{\beta}=-1\cdot\cdot\cdot\cdot\cdot\cdot\cdot (2)\end{array} \)
\(\begin{array}{l}\therefore 2\left(\frac{k^2-2}{k^2-1}\right)(-1)=-5\end{array} \)
\(\begin{array}{l}\Rightarrow k^2 = \frac{1}{3}\end{array} \)
\(\begin{array}{l}\text{and } b = S.R = 2\left(\frac{k^2-2}{k^2-1}\right)-1 = 4\end{array} \)
\(\begin{array}{l}\therefore \frac{b}{k^2}=\frac{4}{\frac{1}{3}}=12\end{array} \)
2. The mean and variance of 10 observation were calculated as 15 and 15 respectively by a student who took by mistake 25 instead of 15 for one observation. Then, the correct standard deviation is ________.
Answer (2)
Sol. Given
\(\begin{array}{l}\frac{\sum_{i=1}^{10}x_i}{10}=15~~~~~~~…(1)\end{array} \)
\(\begin{array}{l}\Rightarrow \sum_{i=1}^{10}x_i = 150\end{array} \)
\(\begin{array}{l}\text{and } \frac{\sum_{i=1}^{10}x_i^2}{10}-15^2 = 15\end{array} \)
\(\begin{array}{l}\Rightarrow \sum_{i=1}^{10}x_i^2=2400\end{array} \)
Replacing 25 by 15 we get
\(\begin{array}{l}\Rightarrow \sum_{i=1}^{9}x_i+25=150\end{array} \)
\(\begin{array}{l}\Rightarrow \sum_{i=1}^{9}x_i = 125\end{array} \)
β΄ Correct mean
\(\begin{array}{l}=\frac{\sum_{i=1}^{9}x_i +15}{10}=\frac{125+15}{10}=14\end{array} \)
Similarly,
\(\begin{array}{l}\sum_{i=1}^{2}x_i^2=2400-25^2=1775\end{array} \)
\(\begin{array}{l}\therefore \text{Correct variance} =\frac{\sum_{i=1}^{9}x_i^2 + 15^2}{10}-14^2\end{array} \)
\(\begin{array}{l}=\frac{1775 + 225}{10}-14^2=4\end{array} \)
\(\begin{array}{l}\therefore \text{ correct S.D.}=\sqrt{4}=2\end{array} \)
3. Let the line \(\begin{array}{l}\frac{x-3}{7}=\frac{y-2}{-1}=\frac{z-3}{-4}\end{array} \)
intersect the plane containing the lines \(\begin{array}{l}\frac{x-4}{1}=\frac{y+1}{-2}=\frac{z}{1}\ \text{and}\ 4ax – y + 5z – 7a = 0 = 2x – 5y – z – 3, a \in \mathbb R\end{array} \)
at the point P(Ξ±, Ξ², Ξ³). Then the value of Ξ± + Ξ² + Ξ³ equals _____.
Answer (12)
Sol. Equation of plane containing the line
4ax – y + 5z – 7a = 0 = 2x – 5y – z – 3 can be written as
\(\begin{array}{l}4ax – y + 5z – 7a + \lambda\left(2x – 5y – z – 3\right) = 0\\ \left(4a + 2\lambda\right) x – \left(1 + 5\lambda\right) y + \left(5 – \lambda\right) z – \left(7a + 3\lambda\right) = 0\end{array} \)
Which i coplanar with the line
\(\begin{array}{l}\frac{x-4}{1}=\frac{y+1}{-2}=\frac{z}{1}\end{array} \)
\(\begin{array}{l}4\left(4a + 2\lambda\right) + \left(1 + 5\lambda\right) – \left(7a + 3\lambda\right) = 0\\ 9a + 10\lambda + 1 = 0 β¦(1)\end{array} \)
\(\begin{array}{l}\left(4a + 2 \lambda \right)1 + \left(1 + 5\lambda \right) 2 + 5 – \lambda = 0\\ 4a + 11 \lambda + 7 = 0 β¦(2)\end{array} \)
\(\begin{array}{l}a = 1, \lambda = – 1\end{array} \)
Equation of plane is x + 2y + 3z β 2 = 0
Intersection with the line
\(\begin{array}{l}\frac{x-3}{7}=\frac{y-2}{-1}=\frac{z-3}{-4}\end{array} \)
(7t + 3) + 2 (βt + 2) + 3 (β 4t + 3) β 2 = 0
β7t + 14 = 0
t = 2
So, the required point is (17, 0, β5)
\(\begin{array}{l}\alpha + \beta + \gamma = 12\end{array} \)
4. An ellipse \(\begin{array}{l}E: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\end{array} \)
passes through the vertices of the hyperbola \(\begin{array}{l}H: \frac{x^2}{49}-\frac{y^2}{64}=-1\end{array} \)
. Let the major and minor axes of the ellipse E coincide with the transverse and conjugate axes of the hyperbola H, respectively. Let the product of the eccentricities of E and H be 1/2. If the length of the latus rectum of the ellipse E, then the value of 113l is equal to _____.
Answer (1552)
Sol. Vertices of hyperbola = (0, Β± 8)
As ellipse pass through it i.e.,
\(\begin{array}{l}0+\frac{64}{b^2}=1 \Rightarrow b^2 = 64~~~~~~~…(1)\end{array} \)
As major axis of ellipse coincide with transverse axis of hyperbola we have b > a i.e.
\(\begin{array}{l}e_E = \sqrt{1-\frac{a^2}{64}}=\frac{\sqrt{64-a^2}}{8}\end{array} \)
\(\begin{array}{l}\text{and } e_H = \sqrt{1+\frac{49}{64}}=\frac{\sqrt{113}}{8}\end{array} \)
\(\begin{array}{l}\therefore e_E\cdot e_H = \frac{1}{2}\frac{\sqrt{64-a^2}\sqrt{113}}{64}\end{array} \)
\(\begin{array}{l}\Rightarrow \left(64 – a^2\right) \left(113\right) = 32^2\end{array} \)
\(\begin{array}{l}\Rightarrow a^2 = 64 – \frac{1024}{113}\end{array} \)
\(\begin{array}{l}\text{L.R of ellipse} = \frac{2a^2}{b}=\frac{2}{8}\left(\frac{113\times 64 – 1024}{113}\right)\end{array} \)
\(\begin{array}{l}=I=\frac{1552}{113}\end{array} \)
\(\begin{array}{l} \therefore 113l = 1552\end{array} \)
5. Let y = y(x) be the solution curve of the differential equation
\(\begin{array}{l}\sin(2x^2)\log_{e} (\tan x^2)dy + \left(4xy -4\sqrt{2}x \sin \left(x^2 – \frac{\pi}{4} \right)\right)dx = 0,\ 0 < x < \sqrt{\frac{\pi}{2}}\end{array} \)
\(\begin{array}{l}\text{which passes through the point}\ \left(\sqrt{\frac{\pi}{6}}, 1\right).\ \text{Then}\ \left|y\left( \sqrt{\frac{\pi}{3}} \right)\right|\end{array} \)
is equal to _______.
Answer (1)
Sol.
\(\begin{array}{l}\frac{dy}{dx}+y\left( \frac{4x}{\sin (2x^2) \ln (\tan x^2)} \right) = \frac{4\sqrt{2} x \sin \left(x^2 – \frac{\pi}{4} \right)}{\sin(2x^2) \ln (\tan x^2)} \end{array} \)
\(\begin{array}{l}\text{I. F} = e^{\int \frac{4x}{\sin(2x^2)\ln (\tan x^2)}dx}\end{array} \)
\(\begin{array}{l}=e^{\ln | \ln (\tan x^2)} = \ln (\tan x^2)\end{array} \)
\(\begin{array}{l}\therefore \int d(y.\ln(\tan x^2 )) = \int \frac{4\sqrt{2}x \sin \left(x^2 – \frac{\pi}{4}\right)}{\sin(2x^2)}dx\end{array} \)
\(\begin{array}{l}\Rightarrow y \ln (tan x^2) = \ln \left|\frac{\sec x^2 + \tan x^2}{\text{cosec~} x^2 – \cot x^2 }\right|+ C\end{array} \)
\(\begin{array}{l}\ln\left(\frac{1}{\sqrt{3}}\right)=\ln \left(\frac{\frac{3}{\sqrt{3}}}{2-\sqrt{3}}\right) + C\end{array} \)
\(\begin{array}{l}e = \ln \left( \frac{1}{\sqrt{3}}\right)-\ln\left(\frac{\sqrt{3}}{2-\sqrt{3}}\right)\end{array} \)
\(\begin{array}{l}\text{For }y\left( \sqrt{\frac{\pi}{3}}\right)\end{array} \)
\(\begin{array}{l}y\ln (\sqrt{3}) = \ln \left| \frac{2+\sqrt{3}}{\frac{2}{\sqrt{3}} + \frac{1}{\sqrt{3}}}\right| + \ln \left(\frac{1}{\sqrt{3}}\right)-\ln \left( \frac{\sqrt{3}}{2\sqrt{3}}\right)\end{array} \)
\(\begin{array}{l}=\ln(2+\sqrt{3}) + \ln \left(\frac{1}{\sqrt{3}}\right)+ \ln\left(\frac{1}{\sqrt{3}}\right) – \ln\left(\frac{\sqrt{3}}{2-\sqrt{3}}\right)\end{array} \)
\(\begin{array}{l}\Rightarrow y \ln \sqrt{3}=\ln\left(\frac{1}{\sqrt{3}}\right)\end{array} \)
\(\begin{array}{l}\Rightarrow \frac{y}{2}\ln3 =-\frac{1}{2}\ln 3\end{array} \)
\(\begin{array}{l}\Rightarrow y = 1\\ \therefore \left|y\left(\sqrt{\frac{\pi}{3}}\right)\right| =1\end{array} \)
6. Let M and N be the number of points on the curve y5 β 9xy + 2x = 0, where the tangents to the curve are parallel to x-axis and y-axis, respectively. Then the value of M + N equals ________.
Answer (2)
Sol. Here equation of curve is
y5 β 9xy + 2x = 0 β¦(i)
On differentiating:
\(\begin{array}{l}5y^4\frac{dy}{dx}-9y-9x\frac{dy}{dx}+2=0\end{array} \)
\(\begin{array}{l}\therefore \frac{dy}{dx}=\frac{9y-2}{5y^4-9x}\end{array} \)
When tangents are parallel to x axis then 9y β 2 = 0
β΄ M = 1.
For tangent perpendicular to x-axis
5y4 β 9x = 0 β¦(ii)
From equation (1) and equation (2) we get only one point.
β΄ N = 1.
β΄ M + N = 2.
7. Let \(\begin{array}{l}f\left(x\right) = 2x^2 – x – 1\ \text{and}\ S=\left\{n\in \mathbb{Z}: |f(n)|\le 800\right\}.\end{array} \)
Β Then, the value of βnβS f(n)Β is equal to ________.
Answer (10620)
Sol.
\(\begin{array}{l}\because \left|f(n)\right|\le 800\end{array} \)
\(\begin{array}{l}\Rightarrow – 800 \le 2n^2 – n -1 \le 800\end{array} \)
\(\begin{array}{l}\Rightarrow 2n^2 – n – 801 \le 0\end{array} \)
\(\begin{array}{l}\therefore n \in \left[\frac{-\sqrt{6409}+1}{4},\frac{\sqrt{6409}+1}{4} \right] \text { and } n \in z\end{array} \)
\(\begin{array}{l}\therefore n = – 19, – 18, – 17,β¦β¦β¦., 19, 20.\end{array} \)
\(\begin{array}{l}\therefore \sum (2x^2-x-1)=2\sum x^2 – \sum x – \sum 1\end{array} \)
\(\begin{array}{l}=2\cdot 2 \cdot (1^2 + 2^2 + …+ 19^2)+2\cdot 20^2 – 20 -40=10620 \end{array} \)
8. Let S be the set containing all 3 Γ 3 matrices with entries from {-1, 0, 1}. The total number of matrices A β S such that the sum of all the diagonal elements of AT A is 6 is ________.
Answer (5376)
Sol. Sum of all diagonal elements is equal to sum of square of each element of the matrix.
\(\begin{array}{l}i.e., A = \begin{bmatrix}a_1 & a_2 & a_3 \\b_1 & b_2 & b_3 \\c_1 & c_2 & c_3 \\\end{bmatrix}\end{array} \)
\(\begin{array}{l}\text{then } t_r(A \cdot A^T)\end{array} \)
\(\begin{array}{l}= a_1^2 + a_2^2 + a_3^2 + b_1^2 + b_2^2 + b_3^2 + c_1^2 + c_2^2 + c_3^2\end{array} \)
\(\begin{array}{l}\because a_i, b_i, c_i \in \{-1, 0, 1\} \text{ for } i = 1,2,3\end{array} \)
β΄ Exactly three of them are zero and rest are 1 or β 1.
Total number of possible matrices
\(\begin{array}{l}^9C_3 \times 2^6\end{array} \)
\(\begin{array}{l}=\frac{9\times 8 \times 7}{6} \times 64= 5376\end{array} \)
9. If the length of the latus rectum of the ellipse x2 + 4y2 + 2x + 8y β Ξ» = 0 is 4, and l is the length of its major axis, then Ξ» + l is equal to ________.
Answer (75)
Sol. Equation of ellipse is: x2 + 4y2 + 2x + 8y β Ξ» = 0
(x + 1)2 + 4 (y + 1)2 = Ξ» + 5
\(\begin{array}{l}\frac{(x+1)^2}{\lambda + 5}+ \frac{(y+1)^2}{\left(\frac{\lambda + 5}{4}\right)}=1\end{array} \)
Length of latus rectum
\(\begin{array}{l}=\frac{2\cdot \left(\frac{\lambda + 5}{4}\right)}{\sqrt{\lambda + 5}} = 4\end{array} \)
\(\begin{array}{l}\therefore \lambda = 59.\end{array} \)
Length of major axis \(\begin{array}{l}= 2\cdot \sqrt{\lambda + 5}=16=l\end{array} \)
\(\begin{array}{l}\therefore \lambda + l = 75\end{array} \)
10. Let \(\begin{array}{l}S=\{z \in \mathbb{C} : z^2 + \bar{z} = 0 \}.\ \text{Then}\ \sum_{z \in S}(Re(z)+Im(z))\end{array} \)
is equal to ________.
Answer (0)
Sol.
\(\begin{array}{l}\because z^2 + \bar{z}=0 \text{ Let } z= x + iy\end{array} \)
\(\begin{array}{l}\therefore x^2 β y^2 + 2ixy + x β iy = 0\\ \left(x^2 β y^2 + x\right) + i\left(2xy β y\right) = 0\end{array} \)
\(\begin{array}{l}\therefore x^2 + y^2 = 0 ~\text{and} \left(2x β 1\right)y = 0\end{array} \)
\(\begin{array}{l}\text{If } x = +\frac{1}{2} \text{ then } y = \pm \frac{\sqrt{3}}{2}\end{array} \)
And if y = 0 then x = 0, β1
\(\begin{array}{l}\therefore z= 0 + 0i, -1 + 0i, \frac{1}{2}+ \frac{\sqrt{3}}{2}i, \frac{1}{2}-\frac{\sqrt{3}}{2}i\end{array} \)
\(\begin{array}{l}\therefore \sum(R_e(z)+ m(z))=0\end{array} \)
JEE Main 2022 July 27th Shift 1 Paper Analysis
Comments