The JEE Main 2022 June 26 – Shift 1 Maths Question Paper with Solutions are given on this page. Revising the JEE Main 2022 question papers will help students to know the pattern and difficulty level of the JEE 2022 exams. These solutions are designed by the expert faculty at BYJU’S. Students can also download the JEE Main 2022 June 26 – Shift 1 Maths Question Paper with Solutions in PDF format. The JEE Main 2022 question paper with solutions will help students evaluate their score in the JEE Main 2022 exam. Students are advised to learn the detailed solutions of the JEE Main 2022 question papers, so that they can score better marks in the upcoming entrance exams.
JEE Main 2022 June 26 – Shift 1 Maths Question Paper with Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. Let
\(\begin{array}{l}f\left ( x \right )=\frac{x-1}{x+1},x\epsilon R-\left\{0,-1,1 \right\}\end{array} \)
If ƒn+1(x) = ƒ(ƒn(x)) for all n∈N, then ƒ6(6) + ƒ7(7) is equal to :
(A)
\(\begin{array}{l}\frac{7}{6}\end{array} \)
(B)
\(\begin{array}{l}-\frac{3}{2}\end{array} \)
(C)
\(\begin{array}{l}\frac{7}{12}\end{array} \)
(D)
\(\begin{array}{l}-\frac{11}{12}\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l}f\left ( x \right )=\frac{x-1}{x+1}\Rightarrow f\left ( f\left ( x \right ) \right )=\frac{\frac{x-1}{x+1}-1}{\frac{x-1}{x+1}+1}=-\frac{1}{x}\end{array} \)
⇒
\(\begin{array}{l}f^3\left ( x \right )=-\frac{x+1}{x-1}\Rightarrow f^4\left (x \right )=-\frac{\frac{x-1}{x+1}+1}{\frac{x-1}{x+1}-1}=x\end{array} \)
So, ƒ6(6) + ƒ7(7) = ƒ2(6) + ƒ3(7)
\(\begin{array}{l}=-\frac{1}{6}-\frac{7+1}{7-1}=-\frac{9}{6}=-\frac{3}{2}\end{array} \)
2. Let
\(\begin{array}{l}A=\left\{\textbf{z}~\epsilon~\textbf{C}:\left|\frac{z+1}{z-1} \right| <1\right\}\end{array} \)
and
\(\begin{array}{l}B=\left\{\textbf{z}~\epsilon~\textbf{C}:arg\left ( \frac{z-1}{z+1} \right ) = \frac{2\pi}{3}\right\}\end{array} \)
Then A∩Bis :
(A) A portion of a circle centred at
\(\begin{array}{l}\left ( 0,~-\frac{1}{\sqrt{3}} \right )\end{array} \)
that lies in the second and third quadrants only
(B) A portion of a circle centred at
\(\begin{array}{l}\left ( 0,~-\frac{1}{\sqrt{3}} \right )\end{array} \)
that lies in the second quadrant only
(C) An empty set
(D) A portion of a circle of radius
\(\begin{array}{l}\frac{2}{\sqrt{3}}\end{array} \)
that lies in the third quadrant only
Answer (B)
Sol.
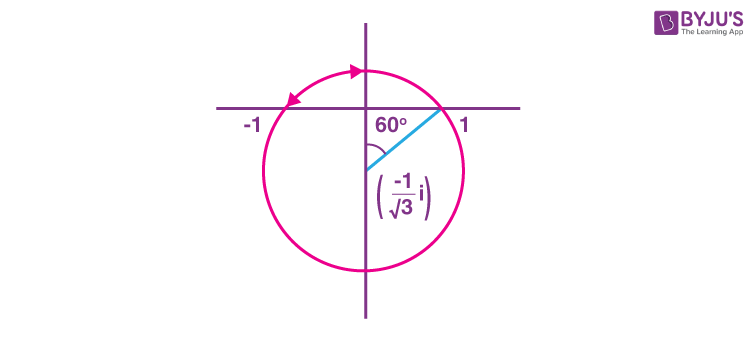
\(\begin{array}{l}\left| \frac{z+1}{z-1}\right|<1\Rightarrow\left| z+1\right|<\left|z-1 \right|\Rightarrow Re\left ( z \right )<0\end{array} \)
and
\(\begin{array}{l}arg\left ( \frac{z-1}{z+1} \right )=\frac{2\pi}{3}\end{array} \)
is a part of circle as shown.
3. Let A be a 3 × 3 invertible matrix. If |adj (24A)| = |adj (3 adj (2A))|, then |A|2 is equal to :
(A) 66
(B) 212
(C) 26
(D) 1
Answer (C)
Sol.
\(\begin{array}{l}\left|adj\left ( 24A \right ) \right|=\left|adj\left ( 3adj\left ( 2A \right ) \right ) \right|\end{array} \)
⇒
\(\begin{array}{l}\left|24A \right|^2=\left|3~adj\left ( 2A \right ) \right|^2\end{array} \)
⇒
\(\begin{array}{l}\left ( 24^3 \right )^2\cdot\left|A \right|^2=\left ( 3^3 \right )^2\left|adj\left ( 2A \right ) \right|^2\end{array} \)
⇒
\(\begin{array}{l}24^6\cdot\left|A \right|^2=3^6\left|2A \right|^4\end{array} \)
⇒
\(\begin{array}{l}24^6\left|A \right|^2=3^6\cdot\left ( 2^3 \right )^4\left|A \right|^4\end{array} \)
⇒
\(\begin{array}{l}\left|A \right|^2=\frac{24^6}{3^6\cdot2^{12}}=\frac{2^{18}.\cdot3^6}{3^6\cdot2^{12}}=2^6\end{array} \)
4. The ordered pair (a, b), for which the system of linear equations
3x – 2y + z = b
5x – 8y + 9z = 3
2x + y + az = –1
has no solution, is :
(A)
\(\begin{array}{l}\left ( 3,\frac{1}{3} \right )\end{array} \)
(B)
\(\begin{array}{l}\left (- 3,\frac{1}{3} \right )\end{array} \)
(C)
\(\begin{array}{l}\left (- 3,-\frac{1}{3} \right )\end{array} \)
(D)
\(\begin{array}{l}\left ( 3,-\frac{1}{3} \right )\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}\begin{vmatrix}3 & -2 & 1 \\5 & -8 & 9 \\2 & 1 & a \\\end{vmatrix}=0\Rightarrow-14a-42=0\Rightarrow a=-3\end{array} \)
Now 3(equation (1)) – (equation (2)) – 2(equation (3)) is
3(3x – 2y + z – b) – (5x – 8y + 9z – 3) – 2(2x + y + az + 1) = 0
⇒ –3b + 3 – 2 = 0
⇒
\(\begin{array}{l}b=\frac{1}{3}\end{array} \)
So for no solution a = –3 and
\(\begin{array}{l}b\neq\frac{1}{3}\end{array} \)
5. The remainder when (2021)2023 is divided by 7 is :
(A) 1
(B) 2
(C) 5
(D) 6
Answer (C)
Sol. 2021 ≡ –2 (mod 7)
⇒ (2021)2023 ≡–(2)2023 (mod 7)
≡ –2(8)674 (mod 7)
≡ –2(1)674 (mod 7)
≡ –2(mod 7)
≡ 5(mod 7)
So when (2021)2023 is divided by 7, remainder is 5.
6.
\(\begin{array}{l}\displaystyle \lim_{x\rightarrow\frac{1}{\sqrt{2}}}\frac{\sin\left ( \cos^{-1}x \right )-x}{1-\tan\left ( \cos^{-1}x \right )}\end{array} \)
is equal to :
(A)
\(\begin{array}{l}\sqrt{2}\end{array} \)
(B)
\(\begin{array}{l}-\sqrt{2}\end{array} \)
(C)
\(\begin{array}{l}\frac{1}{\sqrt{2}}\end{array} \)
(D)
\(\begin{array}{l}-\frac{1}{\sqrt{2}}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l}\lim\limits_{x\rightarrow\frac{1}{\sqrt{2}}}\frac{\sin\left ( \cos^{-1}x \right )-x}{1-\tan\left ( \cos^{-1}x \right )}\end{array} \)
\(\begin{array}{l}\textup{let}~\cos^{-1}x=\frac{\pi}{4}+\theta\end{array} \)
\(\begin{array}{l}=\lim\limits_{\theta\rightarrow0}\frac{\sin\left ( \frac{\pi}{4}+\theta \right )-\cos\left ( \frac{\pi}{4}+\theta \right )}{1-\tan\left ( \frac{\pi}{4}+\theta \right )}\end{array} \)
\(\begin{array}{l}=\lim\limits_{\theta\rightarrow0}\frac{\sqrt{2}\sin\left ( \frac{\pi}{4}+\theta-\frac{\pi}{4} \right )}{1-\frac{1+\tan\theta}{1-\tan\theta}}\end{array} \)
\(\begin{array}{l}=\lim\limits_{\theta\rightarrow0}\frac{\sqrt{2}\sin\theta}{-2\tan\theta}\left ( 1-\tan\theta \right )=-\frac{1}{\sqrt{2}}\end{array} \)
7. g :R→R be two real valued functions defined as
\(\begin{array}{l}f\left ( x \right )=\left\{\begin{matrix}-\left|x+3 \right|, & x<0 \\e^x, & x\geq 0 \\\end{matrix}\right.\end{array} \)
and
\(\begin{array}{l}g\left ( x \right )=\left\{\begin{matrix}x^2+k_1x, & x<0 \\4x+k_2, & x\geq 0 \\\end{matrix}\right.\end{array} \)
where k1 and k2 are real constants. If (goƒ) is differentiable at x = 0, then (goƒ) (–4) + (goƒ) (4) is equal to :
(A) 4(e4 + 1)
(B) 2(2e4 + 1)
(C) 4e4
(D) 2(2e4 – 1)
Answer (D)
Sol. ∵ goƒ is differentiable at x = 0
So R.H.D = L.H.D
\(\begin{array}{l}\frac{d}{dx}\left ( 4e^x+k_2 \right )=\frac{d}{dx}\left ( \left ( -\left|x+3 \right| \right )^2-k_1\left|x+3 \right| \right )\end{array} \)
⇒ 4 = 6 –k1⇒k1 = 2
Also g(ƒ(0+)) = g(ƒ(0–))
⇒ 4 + k2 = 9 – 3k1⇒k2 = –1
Now g(ƒ(–4)) + g(ƒ(4))
= g(–1) + g(e4) = (1 – k1) + (4e4 + k2)
= 4e4 – 2
= 2(2e4 – 1)
8. The sum of the absolute minimum and the absolute maximum values of the function ƒ(x) = |3x – x2 + 2| – x in the interval [–1, 2] is :
(A)
\(\begin{array}{l}\frac{\sqrt{17}+3}{2}\end{array} \)
(B)
\(\begin{array}{l}\frac{\sqrt{17}+5}{2}\end{array} \)
(C) 5
(D)
\(\begin{array}{l}\frac{9-\sqrt{17}}{2}\end{array} \)
Answer (A)
Sol. ƒ(x) = |x2– 3x – 2| – x
\(\begin{array}{l}\forall x\epsilon\left [ -1,2 \right ] \end{array} \)
⇒
\(\begin{array}{l}f\left ( x\right)=\left\{\begin{matrix}x^2-4x-2~~\textup{if}-1\leq x<\frac{3-\sqrt{17}}{2}\\\\ -x^2+2x+2~~\textup{if}~\frac{3-\sqrt{17}}{2}\leq x\leq 2\end{matrix}\right.\end{array} \)
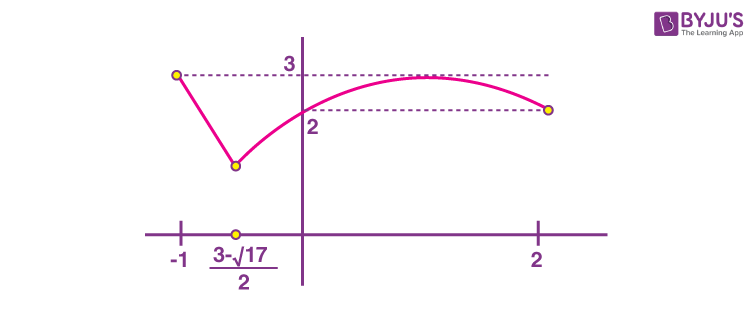
ƒ(x)max = 3
\(\begin{array}{l}f\left ( x \right )_{\textup{min}}=f\left ( \frac{3-\sqrt{17}}{2} \right )\end{array} \)
\(\begin{array}{l}=\frac{\sqrt{17}-3}{2}\end{array} \)
9. Let S be the set of all the natural numbers, for which the line
\(\begin{array}{l}\frac{x}{a}+\frac{y}{b}=2\end{array} \)
is a tangent to the curve \(\begin{array}{l}\left ( \frac{x}{a} \right )^n+\left ( \frac{y}{b} \right )^n=2\end{array} \)
at the point (a, b), ab ≠ 0. Then :
(A) S = ɸ
(B) n(S) = 1
(C) S = {2k : k ∈ N }
(D) S = N
Answer (D)
Sol.
\(\begin{array}{l}\left ( \frac{x}{a} \right )^n+\left ( \frac{y}{b} \right )^n=2\end{array} \)
\(\begin{array}{l}\Rightarrow\frac{n}{a}\left ( \frac{x}{a} \right )^{n-1}+\frac{n}{b}\left ( \frac{y}{b} \right )^{n-1}\frac{dy}{dx}=0\end{array} \)
\(\begin{array}{l}\Rightarrow\frac{dy}{dx}=-\frac{b}{a}\left ( \frac{bx}{ay} \right )^{n-1}\end{array} \)
\(\begin{array}{l}\frac{dy}{dx_{\left (a,b \right )}}=-\frac{b}{a}\end{array} \)
So line always touches the given curve.
10. The area bounded by the curve
\(\begin{array}{l}y=\left|x^2-9 \right|\end{array} \)
and the line y = 3 is
(A)
\(\begin{array}{l}4\left ( 2\sqrt{3}+\sqrt{6}-4 \right )\end{array} \)
(B)
\(\begin{array}{l}4\left ( 4\sqrt{3}+\sqrt{6}-4 \right )\end{array} \)
(C)
\(\begin{array}{l}8\left ( 4\sqrt{3}+3\sqrt{6}-9 \right )\end{array} \)
(D)
\(\begin{array}{l}8\left ( 4\sqrt{3}+\sqrt{6}-9 \right )\end{array} \)
Answer (*)
Sol. y = 3 and y = |x2 – 9|
Intersect in first quadrant at
\(\begin{array}{l}x=\sqrt{6}~\textup{and}~x=\sqrt{12}\end{array} \)
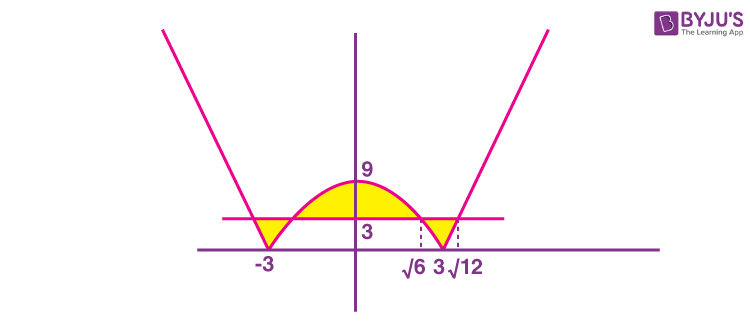
Required area
\(\begin{array}{l}=2\left [ \frac{2}{3}\left ( 6\times\sqrt{6} \right )+\displaystyle\int\limits_{\sqrt{6}}^{3}\left ( 3-\left ( 9-x^2 \right ) \right )dx+\displaystyle\int\limits_3^{\sqrt{12}}\left ( 3-\left ( x^2-9 \right ) \right )dx \right ]\end{array} \)
\(\begin{array}{l}=2\left [ 4\sqrt{6}+\left ( \frac{x^3}{3}-6x \right )\left|_{\sqrt{6}}^{3}+\left ( 12x-\frac{x^3}{3} \right ) \right|_3^{\sqrt{12}} \right ]\end{array} \)
\(\begin{array}{l}=2\left [4\sqrt{6}+\left ( 4\sqrt{6}-9 \right )+\left ( 8\sqrt{12}-27 \right ) \right ]\end{array} \)
\(\begin{array}{l}=2\left [ 8\sqrt{6}+16\sqrt{3}-36 \right ]=8\left [ 2\sqrt{6}+4\sqrt{3}-9 \right ]\end{array} \)
11. Let R be the point (3, 7) and let P and Q be two points on the line x + y = 5 such that PQR is an equilateral triangle, Then the area of ΔPQRis :
(A)
\(\begin{array}{l}\frac{25}{4\sqrt{3}}\end{array} \)
(B)
\(\begin{array}{l}\frac{25\sqrt{3}}{2}\end{array} \)
(C)
\(\begin{array}{l}\frac{25}{\sqrt{3}}\end{array} \)
(D)
\(\begin{array}{l}\frac{25}{2\sqrt{3}}\end{array} \)
Answer (D)
Sol.
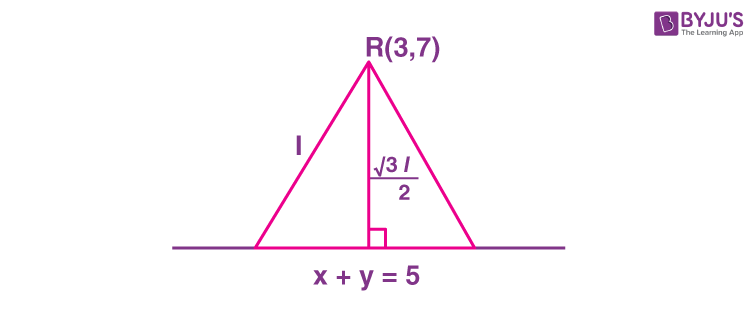
Altitude of equilateral triangle,
\(\begin{array}{l}\frac{\sqrt{3}l}{2}=\frac{5}{\sqrt{2}}\end{array} \)
\(\begin{array}{l}l=\frac{5\sqrt{2}}{\sqrt{3}}\end{array} \)
Area of triangle
\(\begin{array}{l}=\frac{\sqrt{3}}{4}l^2=\frac{\sqrt3}{4}\cdot\frac{50}{3}=\frac{25}{2\sqrt{3}}\end{array} \)
12. Let C be a circle passing through the points
A(2, –1) and B (3, 4). The line segment AB is not a diameter of C. If r is the radius of C and its centre lies on the circle
\(\begin{array}{l}\left ( x-5 \right )^2+\left ( y-1 \right )^2=\frac{13}{2}\end{array} \)
then r2 is equal to :
(A) 32
(B)
\(\begin{array}{l}\frac{65}{2}\end{array} \)
(C)
\(\begin{array}{l}\frac{61}{2}\end{array} \)
(D) 30
Answer (B)
Sol. Equation of perpendicular bisector of AB is
\(\begin{array}{l}y-\frac{3}{2}=-\frac{1}{5}\left ( x-\frac{5}{2} \right )\Rightarrow x+5y=10\end{array} \)
Solving it with equation of given circle,
\(\begin{array}{l}\left ( x-5 \right )^2+\left ( \frac{10-x}{5}-1 \right )^2=\frac{13}{2}\end{array} \)
⇒
\(\begin{array}{l}\left ( x-5 \right )^2\left ( 1+\frac{1}{25} \right )=\frac{13}{2}\end{array} \)
⇒
\(\begin{array}{l}x-5=\pm\frac{5}{2}\Rightarrow x=\frac{5}{2}~\textup{or}~\frac{15}{2}\end{array} \)
But
\(\begin{array}{l}x\neq\frac{5}{2}\end{array} \)
because AB is not the diameter.
So, centre will be
\(\begin{array}{l}\left ( \frac{15}{2},\frac{1}{2} \right )\end{array} \)
Now
\(\begin{array}{l}r^2=\left ( \frac{15}{2}-2 \right )^2+\left ( \frac{1}{2}+1 \right )^2\end{array} \)
\(\begin{array}{l}=\frac{65}{2}\end{array} \)
13. Let the normal at the point P on the parabola
y2 = 6x pass through the point (5, –8). If the tangent at P to the parabola intersects its directrix at the point Q, then the ordinate of the point Q is :
(A) –3
(B)
\(\begin{array}{l}-\frac{9}{4}\end{array} \)
(C)
\(\begin{array}{l}-\frac{5}{2}\end{array} \)
(D) –2
Answer (B)
Sol. Let P(at2, 2at) where
\(\begin{array}{l}a=\frac{3}{2}\end{array} \)
T :yt = x + at2 So point Q is
\(\begin{array}{l}\left ( -a,~at~-\frac{a}{t} \right )\end{array} \)
N :y = –tx + 2at + at3 passes through (5, –8)
\(\begin{array}{l}-8=-5t+3t+\frac{3}{2}t^3\end{array} \)
⇒ 3t3 – 4t + 16 = 0
⇒ (t + 2)(3t2 – 6t + 8) = 0
⇒ t = –2
So ordinate of point Q is
\(\begin{array}{l}-\frac{9}{4}\end{array} \)
14. If the two lines
\(\begin{array}{l}l_1:\frac{x-2}{3}=\frac{y+1}{-2},z=2\end{array} \)
and \(\begin{array}{l}l_2:\frac{x-1}{1}=\frac{2y+3}{\alpha}=\frac{z+5}{2}\end{array} \)
are perpendicular, then an angle between the lines l2 and \(\begin{array}{l}l_3:\frac{1-x}{3}=\frac{2y-1}{-4}=\frac{z}{4}\end{array} \)
is :
(A)
\(\begin{array}{l}\cos^{-1}\left ( \frac{29}{4}\right )\end{array} \)
(B)
\(\begin{array}{l}\sec^{-1}\left ( \frac{29}{4}\right )\end{array} \)
(C)
\(\begin{array}{l}\cos^{-1}\left ( \frac{2}{29} \right )\end{array} \)
(D)
\(\begin{array}{l}\cos^{-1}\left ( \frac{2}{\sqrt{29}} \right )\end{array} \)
Answer (B)
Sol. ∵ l1 and l2 are perpendicular, so
\(\begin{array}{l}3\times1+\left ( -2 \right )\left ( \frac{\alpha}{2} \right )+0\times2=0\end{array} \)
⇒ α = 3
Now angle between l2 and l3,
\(\begin{array}{l}\cos\theta=\frac{1\left ( -3 \right )+\frac{\alpha}{2}\left ( -2 \right )+2\left ( 4 \right )}{\sqrt{1+\frac{\alpha^2}{4}}+4\sqrt{9+4+16}}\end{array} \)
⇒
\(\begin{array}{l}\cos\theta=\frac{\frac{2}{29}}{2}\Rightarrow\theta=\cos^{-1}\left ( \frac{4}{29} \right )=\sec^{-1}\left ( \frac{29}{4} \right )\end{array} \)
15. Let the plane 2x + 3y + z + 20 = 0 be rotated through a right angle about its line of intersection with the plane x – 3y + 5z = 8. If the mirror image of the point
\(\begin{array}{l}\left ( 2,-\frac{1}{2},2 \right )\end{array} \)
in the rotated plane is B( a, b, c),then :
(A)
\(\begin{array}{l}\frac{a}{8}=\frac{b}{5}=\frac{c}{-4}\end{array} \)
(B)
\(\begin{array}{l}\frac{a}{4}=\frac{b}{5}=\frac{c}{-2}\end{array} \)
(C)
\(\begin{array}{l}\frac{a}{8}=\frac{b}{-5}=\frac{c}{4}\end{array} \)
(D)
\(\begin{array}{l}\frac{a}{4}=\frac{b}{5}=\frac{c}{2}\end{array} \)
Answer (A)
Sol. Consider the equation of plane,
P : (2x + 3y + z + 20) + λ(x – 3y + 5z – 8) = 0
P : (2 + λ)x + (3 – 3λ)y + (1 + 5λ)z + (20 – 8λ) = 0
∵ Plane P is perpendicular to 2x + 3y + z + 20 = 0
So, 4 + 2λ + 9 – 9λ + 1 + 5λ = 0
P :9x – 18y + 36z – 36 = 0
Or P :x – 2y + 4z = 4
If image of
\(\begin{array}{l}\left ( 2,-\frac{1}{2},2 \right )\end{array} \)
in plane P is (a, b, c) then
\(\begin{array}{l}\frac{a-2}{1}=\frac{b+\frac{1}{2}}{-2}=\frac{c-2}{4}\end{array} \)
and
\(\begin{array}{l}\left ( \frac{a+2}{2} \right )-2\left ( \frac{b-\frac{1}{2}}{2} \right )+4\left ( \frac{c+2}{2} \right )=4\end{array} \)
Clearly
\(\begin{array}{l}a=\frac{4}{3},b=\frac{5}{6}~\textup{and}~c=-\frac{2}{3}\end{array} \)
So, a :b : c = 8 : 5 : – 4
16. If
\(\begin{array}{l}\vec{a}\cdot\vec{b}=1,\vec{b}\cdot\vec{c}=2~\textup{and}~\vec{c}\cdot\vec{a}=3\end{array} \)
, then the value of \(\begin{array}{l}\left [ \vec{a}\times\left ( \vec{b}\times\vec{c} \right ),\vec{b}\times\left ( \vec{c}\times\vec{a} \right ),\vec{c}\times\left ( \vec{b}\times\vec{a} \right ) \right ]\end{array} \)
is :
(A) 0
(B)
\(\begin{array}{l}-6\vec{a}\cdot\left ( \vec{b}\times\vec{c} \right )\end{array} \)
(C)
\(\begin{array}{l}12\vec{c}\cdot\left ( \vec{a}\times\vec{b} \right )\end{array} \)
(D)
\(\begin{array}{l}-12\vec{b}\cdot\left ( \vec{c}\times\vec{a} \right )\end{array} \)
Answer (A)
Sol. ∵
\(\begin{array}{l}\vec{a}\times\left ( \vec{b}\times\vec{c} \right )=3\vec{b}-\vec{c}=\vec{u}\end{array} \)
\(\begin{array}{l}\vec{b}\times\left ( \vec{c}\times\vec{a} \right )=\vec{c}-2\vec{a}=\vec{v}\end{array} \)
\(\begin{array}{l}\vec{c}\times\left ( \vec{b}\times\vec{a} \right )=3\vec{b}-2\vec{a}=\vec{w}\end{array} \)
∴
\(\begin{array}{l}\vec{u}+\vec{v}=\vec{w}\end{array} \)
So vectors
\(\begin{array}{l}\vec{u},\vec{v}~\textup{and}~\vec{w}\end{array} \)
are coplanar, hence their Scalar triple product will be zero.
17. Let a biased coin be tossed 5 times. If the probability of getting 4 heads is equal to the probability of getting 5 heads, then the probability of getting atmost two heads is:
(A)
\(\begin{array}{l}\frac{275}{6^5}\end{array} \)
(B)
\(\begin{array}{l}\frac{36}{5^4}\end{array} \)
(C)
\(\begin{array}{l}\frac{181}{5^5}\end{array} \)
(D)
\(\begin{array}{l}\frac{46}{6^4}\end{array} \)
Answer (D)
Sol. Let probability of getting head = p
So,
\(\begin{array}{l}^5C_4p^4\left ( 1-p \right )=^5C_5p^5\end{array} \)
⇒
\(\begin{array}{l}p=5\left ( 1-p \right )\Rightarrow p=\frac{5}{6}\end{array} \)
Probability of getting atmost two heads =
\(\begin{array}{l}^5C_0\left ( 1-p \right )^5+^5C_1p\left ( 1-p \right )^4+^5C_2p^2\left ( 1-p \right )^3\end{array} \)
\(\begin{array}{l}=\frac{1+25+250}{6^5}\end{array} \)
\(\begin{array}{l}=\frac{276}{6^5}=\frac{46}{6^4}\end{array} \)
18. The mean of the numbers a, b, 8, 5, 10 is 6 and their variance is 6.8. If M is the mean deviation of the numbers about the mean, then 25 M is equal to:
(A) 60
(B) 55
(C) 50
(D) 45
Answer (A)
Sol. ∵
\(\begin{array}{l}\overline{x}=6=\frac{a+b+8+5+10}{5}\Rightarrow a+b=7\dots\left ( i \right ) \end{array} \)
And
\(\begin{array}{l}\sigma^2=\frac{a^2+b^2+8^2+5^2+10^2}{5}-6^2=6.8\end{array} \)
⇒ a2 + b2 = 25 …(ii)
From (i) and (ii) (a, b) = (3, 4) or (4, 3)
Now mean deviation about mean
\(\begin{array}{l}M=\frac{1}{5}\left ( 3+2+2+1+4 \right )=\frac{12}{5}\end{array} \)
⇒ 25M = 60
19. Let
\(\begin{array}{l}f\left ( x \right )=2\cos^{-1}x+4\cot^{-1}x-3x^2-2x+10,\chi\epsilon\left [ -1,1 \right ]\end{array} \)
If [a, b] is the range of the function,f then 4a – b is equal to :
(A) 11
(B) 11 – π
(C) 11 + π
(D) 15 – π
Answer (B)
Sol.
\(\begin{array}{l}f\left ( x \right )=2\cos^{-1}x+4\cot^{-1}x-3x^2-2x+10\forall x\epsilon\left [ -1,1 \right ]\end{array} \)
⇒
\(\begin{array}{l}f^{‘}\left ( x \right )=-\frac{2}{\sqrt{1-x^2}}-\frac{4}{1+x^2}-6x-2<0~\forall x\epsilon\left [ -1,1 \right ]\end{array} \)
Sof(x) is decreasing function and range of f(x) is
[f(1), f(-1)], which is [π + 5, 5π + 9]
Now 4a – b = 4(π + 5) – (5π + 9)
= 11 – π
20. Let
\(\begin{array}{l}\Delta,\triangledown \epsilon\left\{ \wedge ,\vee \right\}\end{array} \)
be such that \(\begin{array}{l}p\triangledown q\Rightarrow\left ( \left ( p\Delta q \right )\triangledown r \right ) \end{array} \)
is a tautology. Then \(\begin{array}{l}\left ( p\triangledown q \right )\Delta r\end{array} \)
is logically equivalent to :
(A)
\(\begin{array}{l}\left ( p~\Delta~r \right )\vee q\end{array} \)
(B)
\(\begin{array}{l}\left ( p~\Delta~r \right )\wedge q\end{array} \)
(C)
\(\begin{array}{l}\left ( p \wedge r \right )\Delta q\end{array} \)
(D)
\(\begin{array}{l}\left ( p \triangledown r \right )\wedge q\end{array} \)
Answer (A)
Sol. Case-I
If ∇ is same as ∧
Then (p∧q) ⇒ ((pΔq) ∧r) is equivalent to ~ (p∧q) ∨ ((pΔq) ∧r) is equivalent to (~ (p∧q) ∨ (pΔq))∧ (~ (p∧q) ∨r)
Which cannot be a tautology
For both Δ (i.e.∨ or ∧)
Case-II
If ∇ is same as ∨
Then (p∨q) ⇒ ((pΔq) ∨r) is equivalent to
~(p∨q) ∨ (pΔq) ∨r which can be a tautology if Δ is also same as ∨.
Hence both Δ and ∇ are same as ∨.
Now (p∇q) Δr is equivalent to (p∨q∨r).
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. The sum of the cubes of all the roots of the equation x4 – 3x3 –2x2 + 3x +1 = 0 is _______.
Answer (36)
Sol. x4 – 3x3 – x2 – x2 + 3x + 1 = 0
(x2 – 1) (x2 – 3x – 1) = 0
Let the root of x2 – 3x – 1 = 0 be α and β and other two roots of given equation are 1 and –1
So sum of cubes of roots = 13 + (–1)3 + α3 + β3
= (α + β)3 – 3αβ(α + β)
= (3)3 – 3(–1)(3)
= 36
2. There are ten boys B1, B2, …, B10 and five girls G1, G2,…, G5 in a class. Then the number of ways of forming a group consisting of three boys and three girls, if both B1 and B2 together should not be the members of a group, is ________.
Answer (1120)
Sol. Required number of ways = Total ways of selection – ways in which B1 and B2 are present together.
\(\begin{array}{l}=^{10}C_3\cdot^5C_3-^8C_1\cdot^5C_3=10\left ( 120-8 \right ) \end{array} \)
= 1120
3. Let the common tangents to the curves
4(x2 + y2) = 9 and y2 = 4x intersect at the point Q. Let an ellipse, centered at the origin O, has lengths of semi-minor and semi-major axes equal to OQ and 6, respectively. If e and I respectively denote the eccentricity and the length of the latus rectum of this ellipse, then
\(\begin{array}{l}\frac{l}{e^2}\end{array} \)
is equal to ________.
Answer (4)
Sol. Let y = mx + c is the common tangent
So
\(\begin{array}{l}c=\frac{1}{m}=\pm\frac{3}{2}\sqrt{1+m^2}\Rightarrow m^2=\frac{1}{3}\end{array} \)
So equation of common tangents will be
\(\begin{array}{l}y=\pm\frac{1}{\sqrt{3}}x\pm\sqrt{3}\end{array} \)
which intersects at Q(–3, 0)
Major axis and minor axis of ellipse are 12 and 6. So eccentricity
\(\begin{array}{l}e^2=1-\frac{1}{4}=\frac{3}{4}\end{array} \)
and length of latus rectum \(\begin{array}{l}=\frac{2b^2}{a}=3\end{array} \)
Hence
\(\begin{array}{l}\frac{\ell}{e^2}=\frac{3}{3/4}=4\end{array} \)
4. Let
\(\begin{array}{l}f\left ( x \right )=\max\left\{ \left|x+1 \right|,\left|x+2 \right|,\dots\dots,\left|x+5 \right|\right\}\end{array} \)
Then \(\begin{array}{l}\displaystyle\int\limits_{-6}^0f\left ( x \right )dx\end{array} \)
is equal to _______.
Answer (21)
Sol.
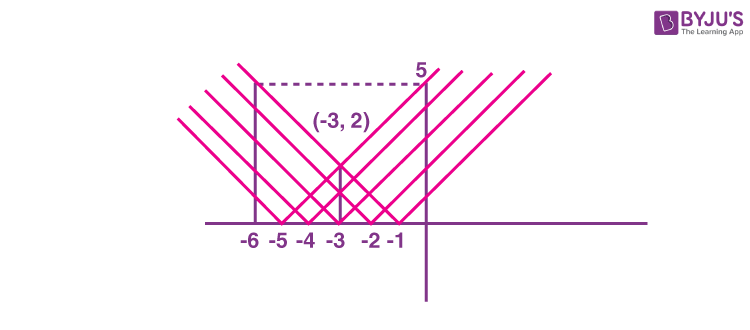
\(\begin{array}{l}\displaystyle\int\limits_{-6}^0f\left ( x \right )dx=2\left [ \frac{1}{2}\left ( 2+5 \right )3 \right ]=21\end{array} \)
5. Let the solution curve y = y(x) of the differential equation (4 + x2)dy – 2x(x2 + 3y + 4)dx = 0 pass through the origin. Then y(2) is equal to _______.
Answer (12)
Sol. (4 + x2) dy – 2x(x2 + 3y + 4)dx = 0
⇒
\(\begin{array}{l}\frac{dy}{dx}=\left ( \frac{6x}{x^2+4} \right )y+2x\end{array} \)
⇒
\(\begin{array}{l}\frac{dy}{dx}-\left ( \frac{6x}{x^2+4} \right )y=2x\end{array} \)
I.F. =
\(\begin{array}{l}e^{-3~\textup{In}\left ( x^2+4 \right )}=\frac{1}{\left ( x^2+4 \right )^3}\end{array} \)
So
\(\begin{array}{l}\frac{y}{\left ( x^2+4 \right )^3}=\int\frac{2x}{\left ( x^2+4 \right )^3}dx+c\end{array} \)
⇒
\(\begin{array}{l}y=-\frac{1}{2}\left ( x^2+4 \right )+c\left ( x^2+4 \right )^3\end{array} \)
When x = 0, y = 0 gives
\(\begin{array}{l}c=\frac{1}{32}\end{array} \)
So, for x = 2,y = 12
6. If sin2(10°)sin(20°)sin(40°)sin(50°)sin(70°)
\(\begin{array}{l}=\alpha-\frac{1}{16}\sin\left ( 10^\circ \right )\end{array} \)
, then 16 + α–1 is equal to _______.
Answer (80)
Sol: (sin10° ⋅ sin50° ⋅ sin70°) ⋅ (sin10° ⋅ sin20° ⋅ sin40°)
=
\(\begin{array}{l}\left ( \frac{1}{4}\sin30^\circ \right )\cdot\left [ \frac{1}{2}\sin10^\circ\left ( \cos20^\circ-\cos60^\circ \right ) \right ]\end{array} \)
=
\(\begin{array}{l}\frac{1}{16}\left [ \sin10^\circ\left ( \cos20^\circ-\frac{1}{2} \right ) \right ]\end{array} \)
=
\(\begin{array}{l}\frac{1}{32}[2\sin10^\circ\cdot\cos20^\circ-\sin10^\circ]\end{array} \)
=
\(\begin{array}{l}\frac{1}{32}[\sin30^\circ-\sin10^\circ-\sin10^\circ]\end{array} \)
=
\(\begin{array}{l}\frac{1}{64}-\frac{1}{16}\sin10^\circ\end{array} \)
Clearly
\(\begin{array}{l}\alpha=\frac{1}{64}\end{array} \)
Hence 16 + α–1 = 80
7. Let A = {n∈N : H.C.F. (n, 45) = 1} and
Let B = {2k :k∈ {1, 2, …,100}}. Then the sum of all the elements of A∩B is ___________.
Answer (5264)
Sol: Sum of all elements of A∩B = 2 [Sum of natural numbers upto 100 which are neither divisible by 3 nor by 5]
=
\(\begin{array}{l}2\left [ \frac{100\times101}{2}-3\left ( \frac{33\times34}{2} \right )-5\left ( \frac{20\times21}{2} \right )+15\left ( \frac{6\times7}{2} \right ) \right ]\end{array} \)
= 10100 – 3366 – 2100 + 630
= 5264
8. The value of the integral
\(\begin{array}{l}\frac{48}{\pi^4}\displaystyle\int\limits_0^\pi\left ( \frac{3\pi x^2}{2}-x^3 \right )\frac{\sin x}{1+\cos^2x}dx\end{array} \)
is equal to ________.
Answer (6)
Sol:
\(\begin{array}{l}I=\frac{48}{\pi^4}\int_{0}^{\pi}\left [ \left ( \frac{\pi}{2}-x \right )^3-\frac{3\pi^2}{4}\left ( \frac{\pi}{2}-x \right )+\frac{\pi^3}{4} \right ]\frac{\sin x~dx}{1+\cos^2x}\end{array} \)
Using
\(\begin{array}{l}\int_a^bf\left ( x \right )dx=\int_a^bf\left ( a+b-x \right )dx\end{array} \)
we get
\(\begin{array}{l}I=\frac{48}{\pi^4}\int_0^\pi\left [ -\left ( \frac{\pi}{2}-x \right )^3+\frac{3\pi^2}{4}\left ( \frac{\pi}{2}-x \right )+\frac{\pi^3}{4} \right ]\frac{\sin~x~dx}{1+\cos^2~x}\end{array} \)
Adding these two equations, we get
\(\begin{array}{l}2I=\frac{48}{\pi^4}\int_0^\pi\frac{\pi^3}{2}\cdot\frac{\sin~x~dx}{1+\cos^2~x}\end{array} \)
⇒
\(\begin{array}{l}I=\frac{12}{\pi}\left [ -\tan^{-1}\left ( \cos x \right ) \right ]_0^\pi=\frac{12}{\pi}\cdot\frac{\pi}{2}=6\end{array} \)
9. Let
\(\begin{array}{l}A=\displaystyle\sum\limits_{i=1}^{10}\displaystyle\sum\limits_{j=1}^{10}\textup{min}\left\{i,j \right\}\end{array} \)
and\(\begin{array}{l}B=\displaystyle\sum\limits_{i=1}^{10}\displaystyle\sum\limits_{j=1}^{10}\textup{max}\left\{i,j \right\}\end{array} \)
. Then A + B is equal to ____________.
Answer (1100)
Sol: Each element of ordered pair {i, j} is either present in A or in B.
So,A + B =Sum of all elements of all ordered pairs {i, j} for 1 ≤i≤ 10 and 1 ≤j≤ 10
= 20 (1 + 2 + 3+…. + 10)
= 1100
10. Let
\(\begin{array}{l}S=\left ( 0,2\pi \right )-\left\{\frac{\pi}{2},\frac{3\pi}{4},\frac{3\pi}{2},\frac{7\pi}{4} \right\}\end{array} \)
. Let y = y(x), x∈S, be the solution curve of the differential equation \(\begin{array}{l}\frac{dy}{dx}=\frac{1}{1+\sin2x},y\left ( \frac{\pi}{4} \right )=\frac{1}{2}\end{array} \)
. If the sum of abscissas of all the points of intersection of the curve y = y(x) with the curve\(\begin{array}{l}y=\sqrt{2}\sin x\end{array} \)
is \(\begin{array}{l}\frac{k\pi}{12}\end{array} \)
, then k is equal to _________.
Answer (42)
Sol:
\(\begin{array}{l}\frac{dy}{dx}=\frac{1}{1+\sin 2x}\end{array} \)
⇒
\(\begin{array}{l}dy=\frac{\sec^2x~dx}{\left ( 1+\tan~x \right )^2}\end{array} \)
⇒
\(\begin{array}{l}y=-\frac{1}{1+\tan x}+c\end{array} \)
When
\(\begin{array}{l}x=\frac{\pi}{4},~~y=\frac{1}{2}~\textup{gives}~~c=1\end{array} \)
So
\(\begin{array}{l}y=\frac{\tan x}{1+\tan x}\Rightarrow y=\frac{\sin x}{\sin x+\cos x}\end{array} \)
Now,
\(\begin{array}{l}y=\sqrt{2}\sin x~~\Rightarrow~~\sin x=0\end{array} \)
or
\(\begin{array}{l}\sin x+\cos x=\frac{1}{\sqrt{2}}\end{array} \)
sinx = 0 gives x = π only.
and
\(\begin{array}{l}\sin x+\cos x=\frac{1}{\sqrt{2}}\Rightarrow\sin\left ( x+\frac{\pi}{4} \right )=\frac{1}{2}\end{array} \)
So
\(\begin{array}{l}x+\frac{\pi}{4}=\frac{5\pi}{6}~~\textup{or}~~\frac{13\pi}{6}\Rightarrow x=\frac{7\pi}{12}~~\textup{or}~~\frac{23\pi}{12}\end{array} \)
Sum of all solutions =
\(\begin{array}{l}\pi+\frac{7\pi}{12}+\frac{23\pi}{12}=\frac{42\pi}{12}\end{array} \)
Hence k = 42.
❑ ❑ ❑
Download PDF Here
















Comments