The JEE Main 2022 July 29 – Shift 1 Maths Question Paper with Solutions is given on this page. Students can use the JEE Main 2022 question paper with solutions to find the solutions in a detailed manner. JEE Main 2022 answer keys are prepared in a step-by-step method so that students can easily learn the tricks used to solve the questions. Revising the JEE Main 2022 question papers will help students to know the important topics, type of questions asked, difficulty level, etc. Check out the JEE Main 2022 July 29 – Shift 1 Maths Question Paper with Solutions given below.
JEE Main 2022 29th July Shift 1 Mathematics Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. Let R be a relation from the set {1, 2, 3, ….., 60} to itself such that R = {(a, b) : b = pq, where p, q≥ 3 are prime numbers}. Then, the number of elements in R is :
(A) 600
(B) 660
(C) 540
(D) 720
Answer (B)
Sol. b can take its values as 9, 15, 21, 33, 39, 51, 57, 25, 35, 55, 49
b can take these 11 values
and a can take any of 60 values
So, number of elements in R = 60 × 11
= 660
2. If z = 2 + 3i, then \(\begin{array}{l}z^5+(\bar{z})^5\end{array} \)
is equal to :
(A) 244
(B) 224
(C) 245
(D) 265
Answer (A)
Sol. z = (2 + 3i)
\(\begin{array}{l} \Rightarrow\ z^5=\left(2+3i\right)\left(\left(2+3i\right)^2\right)^2\end{array} \)
= (2 + 3i) (-5 + 12i)2
= (2 + 3i)(-119 – 120i)
= – 238 – 240i – 357i + 360
= 122 – 597i
\(\begin{array}{l} \overline{z}^5=122+597i\end{array} \)
\(\begin{array}{l} z^5+\overline{z}^5=244\end{array} \)
3. Let A and B be two 3 × 3 non-zero real matrices such that AB is a zero matrix. Then
(A) the system of linear equations AX = 0 has a unique solution
(B) the system of linear equations AX = 0 has infinitely many solutions
(C) B is an invertible matrix
(D) adj(A) is an invertible matrix
Answer (B)
Sol. AB is zero matrix
⇒ |A| = |B| = 0
So neither A nor B is invertible
If |A| = 0
⇒ |adj A| = 0 so adj A is not invertible
AX = 0 is homogeneous system and |A| = 0
So, it is having infinitely many solutions.
4. If \(\begin{array}{l} \frac{1}{\left(20-a\right)\left(40-a\right)}+\frac{1}{\left(40-a\right)\left(60-a\right)}+\cdots + \frac{1}{\left(180-a\right)\left(200-a\right)}=\frac{1}{256},\end{array} \)
then the maximum value of a is :
(A) 198
(B) 202
(C) 212
(D) 218
Answer (C)
Sol.
\(\begin{array}{l} \frac{1}{20}\left(\frac{1}{20-a}-\frac{1}{40-a}+\frac{1}{40-a}-\frac{1}{60-a}+\cdots + \frac{1}{180-a}-\frac{1}{200-a}\right)=\frac{1}{256}\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{1}{20}\left(\frac{1}{20-a}-\frac{1}{200-a}\right)=\frac{1}{256} \end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{1}{20}\left(\frac{180}{\left(20-a\right)\left(200-a\right)}\right)=\frac{1}{256}\end{array} \)
⇒ (20 – a)(200 – a) = 9.256
OR a2 – 220a + 1696 = 0
⇒ a = 212, 8
5. If \(\begin{array}{l} \displaystyle \lim_{x \to 0}\frac{\alpha e^x+\beta e^{-x}+\gamma\sin x}{x\sin^2 x}=\frac{2}{3},\end{array} \)
where α, β, γ∈R, then which of the following is NOT correct?
(A) α2 + β2 + γ2 = 6
(B) αβ + βγ + γα + 1 = 0
(C) αβ2 + βγ2 + γα2 + 3 = 0
(D) α2 – β2 + γ2 = 4
Answer (C)
Sol.
\(\begin{array}{l} \displaystyle \lim_{x \to 0}\frac{\alpha e^x+\beta e^{-x}+\gamma\sin x}{x\sin^2 x}=\frac{2}{3}\end{array} \)
⇒ α + β = 0 (to make indeterminant form) …(i)
Now,
\(\begin{array}{l} \displaystyle \lim_{x \to 0}\frac{\alpha e^x-\beta e^{-x}+\gamma\cos x}{3x^2}=\frac{2}{3}\end{array} \)
(Using L-H Rule)
⇒ α – β + γ = 0 (to make indeterminant form) …(ii)
Now,
\(\begin{array}{l} \displaystyle \lim_{x \to 0}\frac{\alpha e^x+\beta e^{-x}-\gamma\sin x}{6x}=\frac{2}{3} \end{array} \)
(Using L-H Rule)
\(\begin{array}{l} \Rightarrow \frac{\alpha-\beta-\gamma}{6}=\frac{2}{3}\end{array} \)
⇒ α – β – γ = 4 …(iii)
⇒ γ = –2
and (i) + (ii)
2α = –γ
⇒ α = 1 and β = –1
and αβ2 + βγ2 + γα2 + 3 = 1 – 4 – 2 + 3 = –2
6. The integral \(\begin{array}{l} \displaystyle\int\limits_0^\frac{\pi}{2}\frac{1}{3+2\sin x+\cos x}dx \end{array} \)
is equal to
(A) tan–1(2)
\(\begin{array}{l} (\text{B})\ \tan^{-1}\left(2\right)-\frac{\pi}{4}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{1}{2}\tan^{-1}\left(2\right)-\frac{\pi}{8}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{1}{2}\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} I=\displaystyle\int\limits_0^{\pi/2}\frac{1}{3+2\sin x+\cos x}dx\end{array} \)
\(\begin{array}{l} =\displaystyle\int\limits_0^{\pi/2}\frac{\left(1+\tan^2x/2\right)dx}{3\left(1+\tan^2 x/2\right)+2\left(2\tan x/2\right)+\left(1-\tan^2 x/2\right)}\end{array} \)
Let tan x/2 = t ⇒ sec2x/2 dx = 2 dt
\(\begin{array}{l} I=\displaystyle\int\limits_0^1\frac{2dt}{4+2t^2+4t}\end{array} \)
\(\begin{array}{l} =\displaystyle\int\limits_0^1\frac{dt}{t^2+2t+2}=\displaystyle\int\limits_0^1\frac{dt}{\left(t+1\right)^2+1} \end{array} \)
\(\begin{array}{l} \left.=\tan^{-1}\left(t+1\right)\right|_0^1=\tan^{-1}2-\frac{\pi}{4}\end{array} \)
7. Let the solution curve y = y(x) of the differential equation \(\begin{array}{l} \left(1+e^{2x}\right)\left(\frac{dy}{dx}+y\right)=1\end{array} \)
pass through the point (0, π/2). Then, \(\begin{array}{l} \displaystyle \lim_{x \to \infty}e^xy\left(x\right)\end{array} \)
is equal to
\(\begin{array}{l} (\text{A})\ \frac{\pi}{4} \end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{3\pi}{4} \end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{\pi}{2} \end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{3\pi}{2} \end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} \text{D.E.}\left(1+e^{2x}\right)\left(\frac{dy}{dx}+y\right)=1\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{dy}{dx}+y=\frac{1}{1+e^{2x}}\end{array} \)
\(\begin{array}{l} \text{I.F.}=e^{\int 1.dx}=e^x \end{array} \)
∴ Solution
\(\begin{array}{l} e^xy\left(x\right)=\int\frac{e^x}{1+e^{2x}}dx\end{array} \)
\(\begin{array}{l} \Rightarrow\ e^xy\left(x\right)=\tan^{-1}\left(e^x\right)+C \end{array} \)
∵ It passes through
\(\begin{array}{l} \left(0,\frac{\pi}{2}\right), C=\frac{\pi}{2}-\frac{\pi}{4}=\frac{\pi}{4}\end{array} \)
\(\begin{array}{l} \therefore\ \displaystyle \lim_{x \to \infty}e^xy\left(x\right)=\displaystyle \lim_{x \to \infty}\tan^{-1}\left(e^x\right)+\frac{\pi}{4}\end{array} \)
\(\begin{array}{l} =\frac{3\pi}{4}\end{array} \)
8. Let a line L pass through the point intersection of the lines bx + 10y – 8 = 0 and \(\begin{array}{l}2x – 3y = 0, b \in R – \left\{ \frac{4}{3}\right\}.\end{array} \)
If the line L also passes through the point (1, 1) and touches the circle 17(x2 + y2) = 16, then the eccentricity of the ellipse (x2/5) + (y2/5) = 1 is
\(\begin{array}{l} (\text{A})\ \frac{2}{\sqrt{5}} \end{array} \)
\(\begin{array}{l} (\text{B})\ \sqrt{\frac{3}{5}} \end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{1}{\sqrt{5}}\end{array} \)
\(\begin{array}{l} (\text{D})\ \sqrt{\frac{2}{5}}\end{array} \)
Answer (B)
Sol. L1 :bx + 10y – 8 = 0, L2 : 2x – 3y = 0
then L : (bx + 10y – 8) + λ(2x – 3y) = 0
∵ It passes through (1, 1)
∴ b + 2 – λ = 0 ⇒ λ = b + 2
and touches the circle x2 + y2 = 16/17
\(\begin{array}{l} \left|\frac{8^2}{\left(2\lambda+b\right)^2+\left(10-3\lambda\right)^2}\right|=\frac{16}{17}\end{array} \)
\(\begin{array}{l} \Rightarrow\ 4\lambda^2+b^2+4b\lambda+100+9\lambda^2-60\lambda=68\end{array} \)
\(\begin{array}{l} \Rightarrow\ 13\left(b+2\right)^2+b^2+4b\left(b+2\right)-60\left(b+2\right)+32=0 \end{array} \)
\(\begin{array}{l} \Rightarrow\ 18b^2=36\ \therefore b^2=2\end{array} \)
\(\begin{array}{l}\therefore \text{Eccentricity of ellipse}\ \frac{x^2}{5}+\frac{y^2}{b^2}=1\ \text{is}\end{array} \)
\(\begin{array}{l}e=\sqrt{1-\frac{2}{5}}=\sqrt{\frac{3}{5}}\end{array} \)
9. If the foot of the perpendicular from the point A(–1, 4, 3) on the plane P : 2x + my + nz = 4, is (-2, 7/2, 3/2), then the distance of the point A from the plane P, measured parallel to a line with direction ratios 3, –1, –4, is equal to
(A) 1
\(\begin{array}{l} (\text{B})\ \sqrt{26}\end{array} \)
\(\begin{array}{l} (\text{C})\ 2\sqrt{2}\end{array} \)
\(\begin{array}{l} (\text{D})\ \sqrt{14}\end{array} \)
Answer (B)
Sol. (-2, 7/2, 3/2) satisfies the plane P : 2x + my + nz = 4
\(\begin{array}{l} -4+\frac{7m}{2}+\frac{3n}{2}=4\Rightarrow 7m+3n=16\cdots \left(i\right)\end{array} \)
Line joining A(–1, 4, 3) and (-2, 7/2, 3/2) is perpendicular to P : 2x + my + nz = 4
\(\begin{array}{l} \frac{1}{2}=\frac{\frac{1}{2}}{m}=\frac{\frac{3}{2}}{n}\Rightarrow m=1~\&~n=3\end{array} \)
Plane P : 2x + y + 3z = 4
Distance of P from A(–1, 4, 3) parallel to the line
\(\begin{array}{l} \frac{x+1}{3}=\frac{y-4}{-1}=\frac{z-3}{-4}:L\end{array} \)
for point of intersection of P&L
2(3r – 1) + (–r + 4) + 3(–4r + 3) = 4 ⇒r = 1
Point of intersection : (2, 3, –1)
Required distance
\(\begin{array}{l} =\sqrt{3^2+1^2+4^2} \end{array} \)
\(\begin{array}{l} =\sqrt{26}\end{array} \)
10. Let \(\begin{array}{l} \vec{a}=3\hat{i}+\hat{j}\ \text{and}\ \vec{b}=\hat{i}+2\hat{j}+\hat{k}.\end{array} \)
\(\begin{array}{l}\text{Let}\ \vec{c}\ \text{be a vector satisfying}\ \vec{a}\times\left(\vec{b}\times\vec{c}\right)=\vec{b}+\lambda\vec{c}.\end{array} \)
\(\begin{array}{l}\text{If}\ \vec{b}\ \text{and}\ \vec{c}\ \text{are non-parallel},\end{array} \)
then the value of λ is
(A) –5
(B) 5
(C) 1
(D) –1
Answer (A)
Sol.
\(\begin{array}{l} \vec{a}=3\hat{i}+\hat{j}~\& \vec{b}=\hat{i}+2\hat{j}+\hat{k}\end{array} \)
\(\begin{array}{l} \vec{a}\times\left(\vec{b}\times\vec{c}\right) =\left(\vec{a}\cdot\vec{c}\right)\vec{b}-\left(\vec{a}\cdot\vec{b}\right)\vec{c}=\vec{b}+\lambda\vec{c}\end{array} \)
\(\begin{array}{l}\text{If}\ \vec{b}~\& \vec{c}\ \text{are non-parallel},\ \text{then}\end{array} \)
\(\begin{array}{l} \vec{a}\cdot\vec{c}=1~\&~\vec{a}\cdot \vec{b}=-\lambda\end{array} \)
but
\(\begin{array}{l} \vec{a}\cdot\vec{b}=5\Rightarrow \lambda =-5\end{array} \)
11. The angle of elevation of the top of a tower from a point A due north of it is α and from a point B at a distance of 9 units due west of A is \(\begin{array}{l}\cos^{-1}\left(\frac{3}{\sqrt{13}}\right).\end{array} \)
If the distance of the point B from the tower is 15 units, then cot α is equal to :
\(\begin{array}{l} (\text{A})\ \frac{6}{5}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{9}{5}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{4}{3}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{7}{3}\end{array} \)
Answer (A)
Sol.
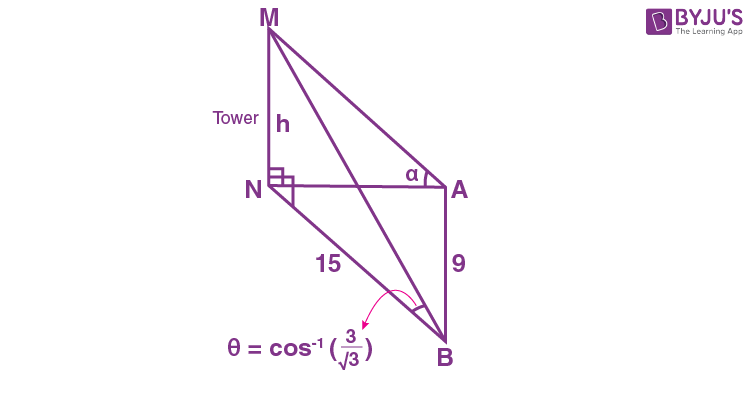
\(\begin{array}{l} NA=\sqrt{15^2-9^2}=12\end{array} \)
\(\begin{array}{l} \frac{h}{15}=\tan\theta=\frac{2}{3}\end{array} \)
h = 10 units
\(\begin{array}{l} \cot\alpha=\frac{12}{10}=\frac{6}{5}\end{array} \)
12. The statement (p∧q) ⇒ (p∧r) is equivalent to :
(A) q⇒ (p∧r)
(B) p⇒ (p∧r)
(C) (p∧r) ⇒ (p∧q)
(D) (p∧q) ⇒ r
Answer (D)
Sol.
|
|
|
A |
B |
|
|
|
|
|
|
|
|
|
| p |
q |
r |
p ∧ q |
p ∧ r |
A → B |
q → B |
p → B |
B → A |
A → r |
| T |
T |
T |
T |
T |
T |
T |
T |
T |
T |
| T |
F |
T |
F |
T |
T |
T |
T |
F |
T |
| F |
T |
T |
F |
F |
T |
F |
T |
T |
T |
| F |
F |
T |
F |
F |
T |
T |
T |
T |
T |
| T |
T |
F |
T |
F |
F |
F |
F |
T |
F |
| T |
F |
F |
F |
F |
T |
T |
F |
T |
T |
| F |
T |
F |
F |
F |
T |
F |
T |
T |
T |
| F |
F |
F |
F |
F |
T |
T |
T |
T |
T |
(p∧ q) ⇒ (p∧ r) is equivalent to (p∧ q) ⇒ r
13. Let the circumcentre of a triangle with vertices A(a, 3), B(b, 5) and C(a, b), ab > 0 be P(1, 1). If the line AP intersects the line BC at the point Q(k1, k2), then k1 + k2 is equal to :
(A) 2
\(\begin{array}{l} (\text{B})\ \frac{4}{7} \end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{2}{7} \end{array} \)
(D) 4
Answer (B)
Sol.
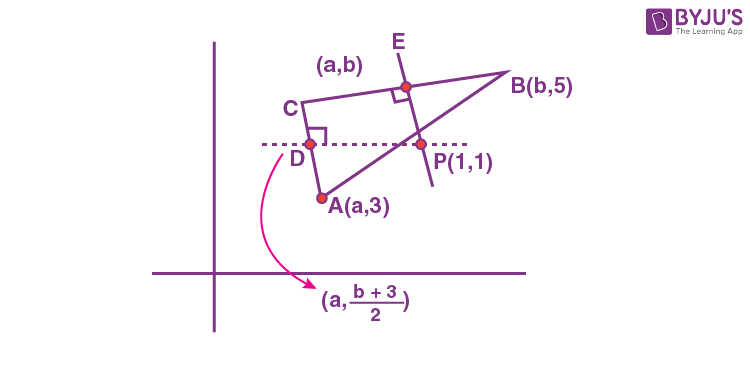
Let D be mid-point of AC, then
\(\begin{array}{l} \frac{b+3}{2}=1\Rightarrow b=-1\end{array} \)
Let E be mid-point of BC,
\(\begin{array}{l} \frac{5-b}{b-a}\cdot\frac{\frac{\left(3+b\right)}{2}}{\frac{a+b}{2}-1}=-1 \end{array} \)
On Putting b = –1, we get a = 5 or –3
But a = 5 is rejected as ab> 0
A(–3, 3), B(–1, 5), C(–3, –1), P(1, 1)
Line BC ⇒ y = 3x + 8
\(\begin{array}{l}Line\ AP\Rightarrow y=\frac{3-x}{2}\end{array} \)
Point of intersection (-13/7, 17/7)
14. Let \(\begin{array}{l} \hat{a}\ \text{and}\ \hat{b}\end{array} \)
be two unit vectors such that the angle between them is π/4. If θ is the angle between the vectors \(\begin{array}{l} \left(\hat{a}+\hat{b}\right)\ \text{and}\ \left(\hat{a}+2\hat{b}+2\left(\hat{a}\times\hat{b}\right)\right),\end{array} \)
then the value of 164 cos2θ is equal to :
\(\begin{array}{l} (\text{A})\ 90+27\sqrt{2}\end{array} \)
\(\begin{array}{l} (\text{B})\ 45+18\sqrt{2}\end{array} \)
\(\begin{array}{l} (\text{C})\ 90+3\sqrt{2}\end{array} \)
\(\begin{array}{l} (\text{D})\ 54+90\sqrt{2}\end{array} \)
Answer (A)
Sol.
\(\begin{array}{l} \hat{a}\cdot\hat{b}=\frac{1}{\sqrt{2}}\text{ and }=\left|\overrightarrow{a}\times\overrightarrow{b}\right|=\frac{1}{\sqrt{2}}\end{array} \)
\(\begin{array}{l} \frac{\left(\hat{a}+\hat{b}\right)\cdot\left(\hat{a}+2\hat{b}+2\left(\hat{a}\times\hat{b}\right)\right)}{\left|\hat{a}+\hat{b}\right|\left|\hat{a}+2\hat{b}+2\left(\hat{a}\times\hat{b}\right)\right|}=\cos\theta\end{array} \)
\(\begin{array}{l} \Rightarrow\ \cos\theta=\frac{1+3\hat{a}\hat{b}+2}{\left|\hat{a}+\hat{b}\right|\left|\hat{a}+2\hat{b}+2\left(\hat{a}\times\hat{b}\right)\right|} \end{array} \)
\(\begin{array}{l} \left|\hat{a}+\hat{b}\right|^2=2+\sqrt{2}\end{array} \)
\(\begin{array}{l} \left|\hat{a}+2\hat{b}+2\left(\hat{a}\times\hat{b}\right)\right|^2=1+4+4\left|\hat{a}\times\hat{b}\right|^2+4\hat{a}\hat{b}\end{array} \)
\(\begin{array}{l} =5+4\cdot\frac{1}{2}+\frac{4}{\sqrt{2}}=7+2\sqrt{2}\end{array} \)
So,
\(\begin{array}{l} \cos^2\theta=\frac{\left(3+\frac{3}{\sqrt{2}}\right)^2}{\left(2+\sqrt{2}\right)\left(7+2\sqrt{2}\right)}=\frac{9\sqrt{2}\left(5\sqrt{2}+3\right)}{164} \end{array} \)
\(\begin{array}{l} \Rightarrow 164\cos^2\theta=90+27\sqrt{2}\end{array} \)
15. If \(\begin{array}{l} f\left(\alpha\right)=\displaystyle\int\limits_1^\alpha\frac{\text{log}_{10}t}{1+t}dt, \alpha > 0,\end{array} \)
then f(e3) + f(e–3) is equal to :
(A) 9
\(\begin{array}{l} (\text{B})\ \frac{9}{2}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{9}{\text{log}_e\left(10\right)}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{9}{2\text{log}_e\left(10\right)}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l} f\left(\alpha\right)=\int_1^\alpha\frac{\text{log}_{10}t}{1+t}dt\cdots\left(i\right)\end{array} \)
\(\begin{array}{l} f\left(\frac{1}{\alpha}\right)=\int_1^\frac{1}{\alpha}\frac{\text{log}_{10}t}{1+t}dt\end{array} \)
Substituting t = 1/p
\(\begin{array}{l} f\left(\frac{1}{\alpha}\right)=\int_1^\alpha\frac{\text{log}_{10}\left(\frac{1}{p}\right)}{1+\frac{1}{p}} \left(\frac{-1}{p^2}\right)dp\end{array} \)
\(\begin{array}{l} =\int_1^\alpha\frac{\text{log}_{10}\ p}{p\left(p+1\right)}dp=\int_1^\alpha\left(\frac{\text{log}_{10}t}{t}-\frac{\text{log}_{10}t}{t+1}\right)dt\cdots\left(ii\right)\end{array} \)
By (i) + (ii)
\(\begin{array}{l} f\left(\alpha\right)+f\left(\frac{1}{\alpha}\right)=\int_1^\alpha\frac{\text{log}_{10}t}{t}dt=\int_1^\alpha\frac{\text{ln}t}{t}\cdot\text{log}_{10}\ e\ dt\end{array} \)
\(\begin{array}{l} =\frac{\left(\text{ln}\alpha\right)^2}{2\text{log}_e10} \end{array} \)
\(\begin{array}{l} \alpha=e^3\Rightarrow f\left(e^3\right)+f\left(e^{-3}\right)=\frac{9}{2\text{log}_e10}\end{array} \)
16. The area of the region \(\begin{array}{l} \left\{\left(x,y\right);\left|x-1\right|\leq y \leq \sqrt{5-x^2} \right\}\end{array} \)
is equal to
\(\begin{array}{l} (\text{A})\ \frac{5}{2}\sin^{-1}\left(\frac{3}{5}\right)-\frac{1}{2}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{5\pi}{4}-\frac{3}{2}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{3\pi}{4}+\frac{3}{2}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{5\pi}{4}-\frac{1}{2}\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l} A=\displaystyle\int\limits_{-1}^1\left(\sqrt{5-x^2}-\left(1-x\right)\right)dx+\displaystyle\int\limits_{1}^2\left(\sqrt{5-x^2}-\left(x-1\right)\right)dx\end{array} \)
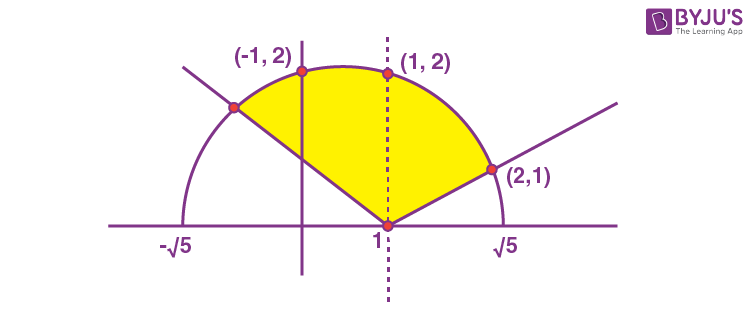
\(\begin{array}{l} \left.A=2\left(\frac{x}{2}\sqrt{5-x^2}+\frac{5}{2}\sin^{-1}\frac{x}{\sqrt{5}}\right)-2x\right|_0^1 \left.+\frac{x}{2}\sqrt{5-x^2}+\frac{5}{2}\sin^{-1}\frac{x}{\sqrt{5}}-\frac{x^2}{2}+x\right|_1^2\end{array} \)
\(\begin{array}{l} =\left(\frac{5\pi}{4}-\frac{1}{2}\right)\text{ sq. units} \end{array} \)
17. Let the focal chord of the parabola P :y2 = 4x along the line L : y = mx + c, m> 0 meet the parabola at the points M and N. Let the line L be a tangent to the hyperbola H :x2 – y2 = 4. If O is the vertex of P and F is the focus of H on the positive x-axis, then the area of the quadrilateral OMFN is
\(\begin{array}{l} (\text{A})\ 2\sqrt{6} \end{array} \)
\(\begin{array}{l} (\text{B})\ 2\sqrt{14} \end{array} \)
\(\begin{array}{l} (\text{C})\ 4\sqrt{6} \end{array} \)
\(\begin{array}{l} (\text{D})\ 4\sqrt{14} \end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} H:\frac{x^2}{4}-\frac{y^2}{4}=1\end{array} \)
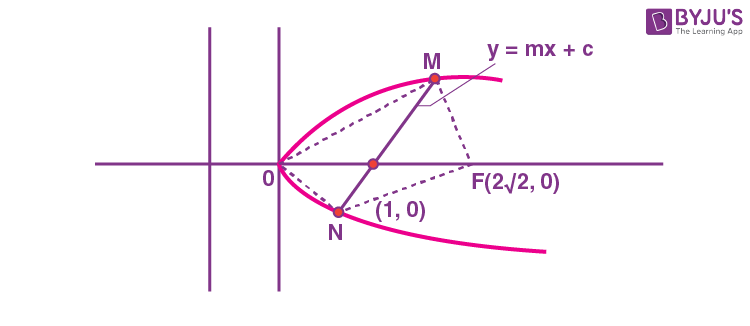
Focus (ae, 0)
\(\begin{array}{l} F\left(2\sqrt{2},0\right) \end{array} \)
y = mx + c passes through (1, 0)
0 = m + c …(i)
L is tangent to hyperbola
\(\begin{array}{l} c=\pm\sqrt{4m^2-4}\end{array} \)
\(\begin{array}{l} -m=\pm\sqrt{4m^2-4}\end{array} \)
m2 = 4m2 – 4
\(\begin{array}{l} m=\frac{2}{\sqrt{3}}\end{array} \)
\(\begin{array}{l} c=\frac{-2}{\sqrt{3}} \end{array} \)
\(\begin{array}{l} T:y=\frac{2}{\sqrt{3}}x-\frac{2}{\sqrt{3}} \end{array} \)
P :y2 = 4x
\(\begin{array}{l} y^2=4\left(\frac{\sqrt{3}y+2}{2}\right)\end{array} \)
\(\begin{array}{l} y^2-2\sqrt{3}y-4 =0\end{array} \)
\(\begin{array}{l}\text{Area}= \frac{1}{2}\begin{vmatrix}0 & 0 \\x_1 & y_1 \\2\sqrt{2} & 0 \\x_2 & y_2 \\0 & 0 \\\end{vmatrix}\end{array} \)
\(\begin{array}{l} =\left|\frac{1}{2}\left(-2\sqrt{2}y_1+2\sqrt{2}y_2\right)\right|\end{array} \)
\(\begin{array}{l} =\sqrt{2}\left|y_2-y_1\right|=\sqrt{2}\sqrt{\left(y_1+y_2\right)^2-4y_1y_2}\end{array} \)
\(\begin{array}{l} =\sqrt{56}\end{array} \)
\(\begin{array}{l} =2\sqrt{14}\end{array} \)
18. The number of points, where the function f: ℝ → ℝ, f(x) = |x – 1|cos|x – 2|sin|x – 1| + (x – 3)|x2 – 5x + 4|, is NOT differentiable, is
(A) 1
(B) 2
(C) 3
(D) 4
Answer (B)
Sol. f :R→R.
f(x) = |x – 1| cos |x – 2| sin |x – 1| + (x – 3) |x2 – 5x + 4|
= |x – 1| cos |x – 2| sin |x – 1| + (x – 3) |x – 1||x – 4|
= |x – 1| [cos |x – 2| sin |x – 1| + (x – 3) |x – 4|]
Sharp edges at x = 1 and x = 4
∴ Non-differentiable at x = 1 and x = 4.
19. Let S = {1, 2, 3, …, 2022}. Then the probability that a randomly chosen number n from the set S such that HCF (n, 2022) = 1, is
\(\begin{array}{l} (\text{A})\ \frac{128}{1011} \end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{166}{1011} \end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{127}{337} \end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{112}{337} \end{array} \)
Answer (D)
Sol. S = {1, 2, 3, …… 2022}
HCF (n, 2022) = 1
⇒n and 2022 have no common factor
Total elements = 2022
2022 = 2 × 3 × 337
M : numbers divisible by 2.
{2, 4, 6, ….., 2022} n(M) = 1011
N : numbers divisible by 3.
{3, 6, 9, ….., 2022} n(N) = 674
L : numbers divisible by 6.
{6, 12, 18, ….., 2022} n(L) = 337
n(M∪N) = n(M) + n(N) –n(L)
= 1011 + 674 – 337
= 1348
0 = Number divisible by 337 but not in M∪N
{337, 1685}
Number divisible by 2, 3 or 337
= 1348 + 2 = 1350
Required probability
\(\begin{array}{l} =\frac{2022-1350}{2022}\end{array} \)
\(\begin{array}{l} =\frac{672}{2022} \end{array} \)
\(\begin{array}{l} =\frac{112}{337} \end{array} \)
20. Let \(\begin{array}{l} f\left(x\right)=3^{\left(x^2-2\right)^3+4},x\in \mathbb{R}.\end{array} \)
Then which of the following statements are true?
P :x = 0 is a point of local minima of f
Q: x = √2 is a point of inflection of f
R :f ′ is increasing for x > √2
(A) Only P and Q
(B) Only P and R
(C) Only Q and R
(D) All P, Q and R
Answer (D)
Sol.
\(\begin{array}{l} f\left(x\right)=3^{\left(x^2-2\right)^3+4}, x\in R \end{array} \)
\(\begin{array}{l} f\left(x\right)=81.3^{\left(x^2-2\right)^3} \end{array} \)
\(\begin{array}{l} f’\left(x\right)=81.3^{\left(x^2-2\right)^3}\text{ln}2.3\left(x^2-2\right)2x\end{array} \)
\(\begin{array}{l} =\left(486\ \text{ln}2\right)\left(3^{\left(x^2-2\right)^3}\left(x^2-2\right)x\right)\end{array} \)
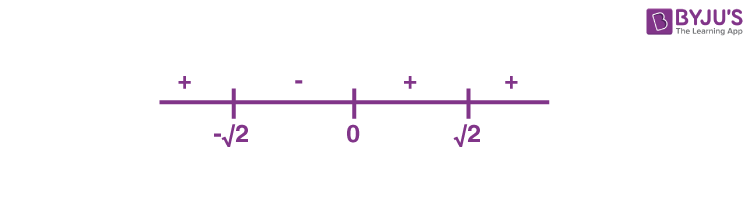
⇒ x = 0 is the local minima.
f′′(x) = (486 ln2)
\(\begin{array}{l} \begin{pmatrix}3^{\left(x^2-2\right)^3}\cdot\left(x^2-2\right) \\\left(5x^2-2+6x^2\text{ln}3\left(x^2-2\right)\right)\end{pmatrix}\end{array} \)
\(\begin{array}{l} f”\left(x\right)=0~~~~~x=\sqrt{2}\end{array} \)
\(\begin{array}{l} f”\left(\sqrt{2}^+\right)>0\end{array} \)
\(\begin{array}{l} f”\left(\sqrt{2}^-\right)<0\end{array} \)
\(\begin{array}{l} \Rightarrow x=\sqrt{2}\end{array} \)
is point of inflection
\(\begin{array}{l} f”\left(x\right)>0~\forall~x>\sqrt{2}\end{array} \)
⇒ f′(x) is increasing for x > √2
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. Let S = {θ ∈ (0, 2π) : 7 cos2θ – 3 sin2θ – 2 cos22θ = 2}. Then, the sum of roots of all the equations x2 – 2 (tan2θ + cot2θ) x + 6 sin2θ = 0, θ ∈ S, is _______.
Answer (16)
Sol. 7 cos2θ – 3 sin2θ – 2 cos22θ = 2
\(\begin{array}{l} \Rightarrow 4\left(\frac{1+\cos2\theta}{2}\right)+3\cos2\theta-2\cos^22\theta=2 \end{array} \)
⇒ 2 + 5 cos2θ – 2 cos2 2θ = 2
⇒ cos 2θ = 0 or 5/2 (rejected)
\(\begin{array}{l} \Rightarrow \cos2\theta=0=\frac{1-\tan^2\theta}{1+\tan^2\theta}\Rightarrow \tan^2\theta =1\end{array} \)
∴ Sum of roots = 2 (tan2θ + cot2θ) = 2 × 2 = 4
But as tanθ = ±1 for π/4, 3π/4, 5π/4, 7π/4 in the interval (0, 2π)
∴ Four equations will be formed
Hence, sum of roots of all the equations
= 4 × 4 = 16.
2. Let the mean and the variance of 20 observations x1, x2,…., x20 be 15 and 9, respectively. For a ∈ R, if the mean of (x1 + α)2, (x2 + α)2,….,(x20 + α)2 is 178, then the square of the maximum value of α is equal to ___________.
Answer (4)
Sol. Given
\(\begin{array}{l} \displaystyle\sum\limits_{\frac{i=1}{20}}^{20}x_i=15\Rightarrow\ \displaystyle\sum\limits_{i=1}^{20}x_i=300\cdots\left(1\right)\end{array} \)
and
\(\begin{array}{l} \displaystyle\sum\limits_{\frac{i=1}{20}}^{20}x_i^2-\left(\overline{x}\right)^2=9\Rightarrow \displaystyle\sum\limits_{i=1}^{20}x_i^2=4680\cdots\left(2\right)\end{array} \)
\(\begin{array}{l} \text{Mean}=\frac{\left(x_1+\alpha\right)^2+\left(x_2+\alpha\right)^2+\cdots+\left(x_{20}+\alpha\right)^2}{20} \end{array} \)
= 178
\(\begin{array}{l} \Rightarrow\ \frac{\displaystyle\sum\limits_{i=1}^{20}x_i^2+2\alpha\displaystyle\sum\limits_{i=1}^{20}x_i+20\alpha^2}{20}=178\end{array} \)
⇒ 4680 + 600α + 20α2 = 3560
⇒ α2 + 30α + 56 = 0
⇒ α2 + 28α + 2α + 56 = 0
⇒ (α + 28)(α + 2) = 0
αmax = – 2
\(\begin{array}{l}\Rightarrow \alpha_{\text{max}}^2=4\end{array} \)
3. Let a line with direction ratios a, – 4a, –7 be perpendicular to the lines with direction ratios 3, – 1, 2b and b, a, – 2. If the point of intersection of the line \(\begin{array}{l} \frac{x+1}{a^2+b^2}=\frac{y-2}{a^2-b^2}=\frac{z}{1} \end{array} \)
and the plane x – y + z = 0 is (α, β, γ), then α + β + γ is equal to ______.
Answer (10)
Sol. Given a.3 + (– 4a)(–1) + (–7) 2b = 0 …(1)
and ab –4a2 + 14 = 0 …(2)
⇒ a2 = 4 and b2 = 1
\(\begin{array}{l} \therefore\ \text{Line }L\equiv\frac{x+1}{5}=\frac{y-2}{3}=\frac{z}{1}=\lambda(\text{ say})\end{array} \)
⇒ General point on line is (5λ – 1, 3λ + 2, λ)
for finding point of intersection with x – y + z = 0
we get (5λ – 1) – (3λ + 2) + (λ) = 0
⇒ 3λ – 3 = 0 ⇒λ = 1
∴ Point at intersection (4, 5, 1)
∴ α + β + γ = 4 + 5 + 1 = 10
4. Let a1, a2, a3,…. be an A.P. If \(\begin{array}{l} \displaystyle\sum\limits_{r=1}^\infty\frac{a_r}{2^r}=4,\end{array} \)
then 4a2 is equal to ________.
Answer (16)
Sol. Given
\(\begin{array}{l} S=\frac{a_1}{2}+\frac{a_2}{2^2}+\frac{a_3}{2^3}+\frac{a_4}{2^4}+\cdots\infty\end{array} \)
\(\begin{array}{l} \frac{\frac{1}{2}S=~~\frac{a_1}{2^2}+\frac{a_2}{2^3}+\cdots\infty}{\frac{S}{2}~~=\frac{a_1}{2}+\frac{\left(a_2+a_1\right)}{2^2}+\frac{\left(a_3+a_2\right)}{2^3}}+\cdots\infty\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{S}{2}=\frac{a_1}{2}+\frac{d}{2}\end{array} \)
⇒ a1 + d = a2 = 4 ⇒ 4a2 = 16
5. Let the ratio of the fifth term from the beginning to the fifth term from the end in the binomial expansion of \(\begin{array}{l} \left(\sqrt[4]2{}+\frac{1}{\sqrt[4]{3}}\right)^n,\ \text{in the increasing powers of}\ \frac{1}{\sqrt[4]{3}}\ \text{be}\ \sqrt[4]{6}:1.\end{array} \)
\(\begin{array}{l}\text{If the sixth term from the beginning is}\ \frac{\alpha}{\sqrt[4]{3}},\end{array} \)
then α is equal to ___________.
Answer (84)
Sol. Fifth term from beginning
\(\begin{array}{l} =^nC_4\left(2^\frac{1}{4}\right)^{n-4}\left(3^\frac{-1}{4}\right)^4\end{array} \)
Fifth term from end = (n – 5 + 1)th term from begin
\(\begin{array}{l} =^nC_{n-4}\left(2^\frac{1}{4}\right)^3\left(3^\frac{-1}{4}\right)^{n-4} \end{array} \)
Given
\(\begin{array}{l} \frac{^nC_42^{\frac{n-4}{4}}\cdot3^{-1}}{^nC_{n-3}2^\frac{4}{4}\cdot3^{-\left(\frac{n-4}{4}\right)}}=6^\frac{1}{4} \end{array} \)
\(\begin{array}{l} \Rightarrow 6^\frac{n-8}{4}=6^\frac{1}{4}\end{array} \)
\(\begin{array}{l} \Rightarrow \frac{n-8}{4}=\frac{1}{4}~~\Rightarrow n=9\end{array} \)
\(\begin{array}{l} T_6=T_{5+1}={^9C_5}\left(2^\frac{1}{4}\right)^4\left(3^\frac{-1}{4}\right)^5\end{array} \)
\(\begin{array}{l} =\frac{^9C_5\cdot2}{3^\frac{1}{4}\cdot 3}=\frac{84}{3^\frac{1}{4}}=\frac{\alpha}{3^\frac{1}{4}} \end{array} \)
⇒ α = 84.
6. The number of matrices of order 3 × 3, whose entries are either 0 or 1 and the sum of all the entries is a prime number, is _________.
Answer (282)
Sol. In a 3 × 3 order matrix there are 9 entries.
These nine entries are zero or one.
The sum of positive prime entries are 2, 3, 5 or 7.
Total possible matrices
\(\begin{array}{l} =\frac{9!}{2!\cdot7!}+\frac{9!}{3!\cdot6!}+\frac{9!}{5!\cdot4!}+\frac{9!}{7!\cdot2!}\end{array} \)
= 36 + 84 + 126 + 36
= 282
7. Let p and p + 2 be prime numbers and let
\(\begin{array}{l} \Delta=\begin{vmatrix}p! & \left(p+1\right)! & \left(p+2\right)! \\\left(p+1\right)! & \left(p+2\right)! & \left(p+3\right)! \\\left(p+2\right)! & \left(p+3\right)! & \left(p+4\right)! \\\end{vmatrix} \end{array} \)
Then the sum of the maximum values of α and β, such that pα and (p + 2)β divide Δ, is _______.
Answer (04)
Sol.
\(\begin{array}{l} \Delta=\begin{vmatrix}p! & \left(p+1\right)! & \left(p+2\right)! \\\left(p+1\right)! & \left(p+2\right)! & \left(p+3\right)! \\\left(p+2\right)! & \left(p+3\right)! & \left(p+4\right)! \\\end{vmatrix} \end{array} \)
\(\begin{array}{l} =p!\left(p+1\right)!\cdot\left(p+2\right)!\begin{vmatrix}1 & p+1 & \left(p+1\right)\left(p+2\right) \\1 & \left(p+2\right) & \left(p+2\right)\left(p+3\right) \\1 & \left(p+3\right) & \left(p+3\right)\left(p+4\right) \\\end{vmatrix}\end{array} \)
\(\begin{array}{l} =p!\left(p+1\right)!\cdot\left(p+2\right)!\begin{vmatrix}1 & p+1 & p^2+3p+2 \\0 & 1 & 2p+4 \\0 & 1 & 2p+6 \\\end{vmatrix}\end{array} \)
\(\begin{array}{l} =2\left(p!\right)\cdot\left(\left(p+1\right)!\right)\cdot\left(\left(p+2\right)!\right)\end{array} \)
\(\begin{array}{l} =2\left(p+1\right)\cdot\left(p!\right)^2\cdot\left(\left(p+2\right)!\right) \end{array} \)
\(\begin{array}{l} =2\left(p+1\right)^2\cdot\left(p!\right)^3\cdot\left(\left(p+2\right)!\right)\end{array} \)
∴ Maximum value of α is 3 and β is 1.
∴ α + β = 4
8. If \(\begin{array}{l}\frac{1}{2\times3\times4}+\frac{1}{3\times4\times5}+\frac{1}{4\times5\times6}+\cdots,+\frac{1}{100\times101\times102}=\frac{k}{101},\end{array} \)
then 34 k is equal to ____________.
Answer (286)
Sol.
\(\begin{array}{l} S=\frac{1}{2\times3\times4}+\frac{1}{3\times4\times5}+\frac{1}{4\times5\times6} +\cdots+\frac{1}{100\times101\times102}\end{array} \)
\(\begin{array}{l} =\frac{1}{\left(3-1\right)\cdot1}\left[\frac{1}{2\times3}-\frac{1}{101\times102}\right]\end{array} \)
\(\begin{array}{l} =\frac{1}{2}\left(\frac{1}{6}-\frac{1}{101\times102}\right)\end{array} \)
\(\begin{array}{l} =\frac{143}{102\times101}=\frac{k}{101}\end{array} \)
∴ 34k = 286
9. Let S = {4, 6, 9} and T = {9, 10, 11, …,1000}. If A = {a1 + a2 + … +ak :k∈N, a1, a2, a3, …, ak∈S}, then the sum of all the elements in the set T – A is equal to ____________.
Answer (11.00)
Sol. Here S = {4, 6, 9}
And T = {9, 10, 11, ……., 1000}.
We have to find all numbers in the form of
4x + 6y + 9z, where x, y, z∈ {0, 1, 2, …..}.
If a and b are coprime number then the least number from which all the number more than or equal to it can be express as ax + by where x, y∈ {0, 1, 2, ….} is (a – 1) · (b – 1).
Then for 6y + 9z = 3(2y + 3z)
All the number from (2 – 1) · (3 – 1) = 2 and above can be express as 2x + 3z (say t).
Now 4x + 6y + 9z = 4x + 3(t + 2)
= 4x + 3t + 6
again by same rule 4x + 3t, all the number from
(4 – 1) (3 – 1) = 6 and above can be express from 4x + 3t.
Then 4x + 6y + 9z express all the numbers from 12 and above.
again 9 and 10 can be express in form 4x + 6y + 9z.
Then set A = {9, 10, 12, 13, …., 1000}.
Then T – A = {11}
Only one element 11 is there.
Sum of elements of T – A = 11
10. Let the mirror image of a circle c1 :x2 + y2 – 2x – 6y + α = 0 in line y = x + 1 be c2 : 5x2 + 5y2 + 10gx + 10fy + 38 = 0. If r is the radius of circle c2, then α + 6r2 is equal to _________.
Answer (12)
Sol. c1: x2 + y2 – 2x – 6y + α = 0
Then centre = (1, 3) and
\(\begin{array}{l}\text{radius}\ (r)= \sqrt{10-\alpha}\end{array} \)
Image of (1, 3) w.r.t. line x – y + 1 = 0 is (2, 2)
c2: 5x2 + 5y2 + 10gx + 10fy + 38 = 0
or
\(\begin{array}{l} x^2+y^2+2gx+2fy+\frac{38}{5}=0 \end{array} \)
Then (–g, –f) = (2, 2)
∴ g = f = – 2 …(i)
\(\begin{array}{l}\text{Radius of}\ c_2=r=\sqrt{4+4-\frac{38}{5}}=\sqrt{10-\alpha} \end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{2}{5}=10-\alpha\end{array} \)
\(\begin{array}{l} \therefore\ \alpha = \frac{48}{5}\text{ and }r=\sqrt{\frac{2}{5}} \end{array} \)
\(\begin{array}{l} \therefore\ \alpha+6r^2=\frac{48}{5}+\frac{12}{5}\end{array} \)
= 12
JEE Main 2022 July 29th Shift 1 Paper Analysis














Comments