The JEE Main 2022 July 27 – Shift 2 Maths Question Paper with Solutions is given on this page. Students are advised to solve the JEE Main 2022 question papers to find out their weak topics and concentrate more on them. Experts at BYJU’S have created the error-free JEE Main 2022 answer keys. Students can revise the JEE Main 2022 question paper with solutions to prepare for any engineering entrance exam.
JEE Main 2022 July 27th Shift 2 Mathematics Question Paper and Solutions
SECTION – A
Multiple Choice Questions: This section contains 20 multiple choice questions. Each question has 4 choices (1), (2), (3) and (4), out of which ONLY ONE is correct.
Choose the correct answer :
1. The domain of the function \(\begin{array}{l} f\left(x\right)=\sin^{-1}\left[2x^2-3\right]+\text{log}_2\left(\text{log}_\frac{1}{2}\left(x^2-5x+5\right)\right) \end{array} \)
where [t] is the greatest integer function, is
\(\begin{array}{l} (\text{A})\ \left(-\sqrt{\frac{5}{2}},\frac{5-\sqrt{5}}{2}\right)\end{array} \)
\(\begin{array}{l} (\text{B})\ \left(\frac{5-\sqrt{5}}{2},\frac{5+\sqrt{5}}{2}\right)\end{array} \)
\(\begin{array}{l} (\text{C})\ \left(1, \frac{5-\sqrt{5}}{2}\right)\end{array} \)
\(\begin{array}{l} (\text{D})\ \left(1, \frac{5+\sqrt{5}}{2}\right)\end{array} \)
Answer (C)
Sol.
| -1 ≤ 2x2 – 3 < 2
or
2 ≤ 2x2 < 5
or
1 ≤ x2 < 5/2
\(\begin{array}{l}x\in \left(-\sqrt{\frac{5}{2}},-1\right]\cup\left[1,\sqrt{\frac{5}{2}}\right)\end{array} \) |
\(\begin{array}{l}\log_{\frac{1}{2}}(x^2-5x+5)>0\end{array} \)
0 < x2 – 5x + 5 < 1x2 – 5x + 5 > 0 & x2 – 5x + 4 < 0
\(\begin{array}{l}x\in \left(-\infty,\frac{5-\sqrt{5}}{2}\right)\cup\left(\frac{5+\sqrt{5}}{2},\infty\right)\end{array} \)
& x ∈ (-∞, 1) U (4, ∞) |
Taking intersection
\(\begin{array}{l} x\in \left(1,\frac{5-\sqrt{5}}{2}\right)\end{array} \)
2. Let S be the set of (α, β), π < α, β < 2π, for which the complex number \(\begin{array}{l} \frac{1-i\sin\alpha}{1+2i\sin\alpha}\ \text{is purely imaginary and}\ \frac{1+i\cos\beta}{1-2i\cos\beta}\ \text{is purely real},\end{array} \)
\(\begin{array}{l}\text{Let}\ Z_{\alpha \beta} = sin 2\alpha + i cos 2\beta, \left(\alpha, \beta\right) \in S.\ \text{Then}\end{array} \)
\(\begin{array}{l} \sum_{\left(\alpha,\beta\right)\in S}\left(iZ_{\alpha\beta}+\frac{1}{i\overline{Z}_{\alpha\beta}}\right)\end{array} \)
is equal to
(A) 3
(B) 3i
(C) 1
(D) 2 – i
Answer (C)
Sol.
\(\begin{array}{l} \because \frac{1-i\sin\alpha}{1+2i\sin\alpha} \text{is purely imaginary} \end{array} \)
\(\begin{array}{l} \therefore\ \frac{1-i\sin\alpha}{1+2i\sin\alpha}+\frac{1+i\sin\alpha}{1-2i\sin\alpha}=0 \end{array} \)
\(\begin{array}{l}\Rightarrow 1 – 2 sin^2 \alpha = 0\end{array} \)
\(\begin{array}{l} \therefore\ \alpha=\frac{5\pi}{4},\frac{7\pi}{4} \end{array} \)
and
\(\begin{array}{l} \frac{1+i\cos\beta}{1-2i\cos\beta}\end{array} \)
is purely real
\(\begin{array}{l} \frac{1+i\cos\beta}{1-2i\cos\beta}-\frac{1-i\cos\beta}{1+2i\cos\beta}=0 \end{array} \)
\(\begin{array}{l}\Rightarrow cos \beta = 0\end{array} \)
\(\begin{array}{l} \therefore \beta =\frac{3\pi}{2}\end{array} \)
\(\begin{array}{l} \therefore S=\left\{\left(\frac{5\pi}{4},\frac{3\pi}{2}\right),\left(\frac{7\pi}{4},\frac{3\pi}{2}\right) \right\}\end{array} \)
Zαβ = 1 – i and Zαβ = –1 – i
\(\begin{array}{l} \therefore\ \sum_{\left(\alpha,\beta\right)\in s}\left(iZ_{\alpha\beta}+\frac{1}{i\overline{Z}\alpha\beta}\right)=i\left(-2i\right)+\frac{1}{i}\left[\frac{1}{1+i}+\frac{1}{-1+i}\right]\end{array} \)
\(\begin{array}{l} =2+\frac{1}{i}\frac{2i}{-2}=1\end{array} \)
3. If α, β are the roots of the equation \(\begin{array}{l} x^2-\left(5+3^{\sqrt{\text{log}_35}}-5^{\sqrt{\text{log}_53}}\right)+3\left(3^{\left(\text{log}_35\right)^{\frac{1}{3}}}-5^{\left(\text{log}_53\right)^{\frac{2}{3}}}-1\right)=0\end{array} \)
then the equation, whose roots are α + 1/β and β + 1/α , is
(A) 3x2 – 20x – 12 = 0
(B) 3x2 – 10x – 4 = 0
(C) 3x2 – 10x + 2 = 0
(D) 3x2 – 20x + 16 = 0
Answer (B)
Sol.
\(\begin{array}{l} 3^{\sqrt{\text{log}_35}}-5^{\sqrt{\text{log}_53}}=3^{\sqrt{\text{log}_35}}-\left(3^{\text{log}_35}\right)^{\sqrt{\text{log}_53}}= 0 \end{array} \)
\(\begin{array}{l} 3^{\left(\text{log}_35\right)^\frac{1}{3}}-5^{\left(\text{log}_53\right)^\frac{2}{3}}=5^{\left(\text{log}_53\right)^\frac{2}{3}}-5^{\left(\text{log}_53\right)^\frac{2}{3}}= 0 \end{array} \)
Note: In the given equation ‘x’ is missing.
So α, β are the roots of x2 – 5x + 3(-1) = 0
\(\begin{array}{l} \alpha+\beta+\frac{1}{\alpha}+\frac{1}{\beta}=\left(\alpha+\beta\right)+\frac{\alpha+\beta}{\alpha\beta}\end{array} \)
\(\begin{array}{l} =5-\frac{5}{3}=\frac{10}{3} \end{array} \)
\(\begin{array}{l} \left(\alpha+\frac{1}{\beta}\right)\left(\beta+\frac{1}{\alpha}\right)=2+\alpha\beta+\frac{1}{\alpha\beta}=2-3-\frac{1}{3}\end{array} \)
\(\begin{array}{l} =\frac{-4}{3} \end{array} \)
So Equation must be option (B).
4. Let \(\begin{array}{l} A=\begin{pmatrix}4 & -2 \\\alpha & \beta \\\end{pmatrix}\end{array} \)
If A2 + γA + 18I = 0, then det (A) is equal to ______.
(A) –18
(B) 18
(C) –50
(D) 50
Answer (B)
Sol. Characteristic equation of A is given by
\(\begin{array}{l}\left|A – \lambda I\right| = 0\end{array} \)
\(\begin{array}{l} \begin{vmatrix}4-\lambda & -2 \\\alpha & \beta-\lambda \\\end{vmatrix}=0\end{array} \)
\(\begin{array}{l}\Rightarrow \lambda^2 – \left(4 + \beta \right)\lambda + \left(4\beta + 2\alpha\right) = 0\end{array} \)
\(\begin{array}{l}So, A^2 – \left(4 + \beta \right)A + \left(4 \beta + 2 \alpha \right)I = 0\end{array} \)
\(\begin{array}{l}\left|A\right| = 4\beta + 2 \alpha = 18\end{array} \)
5. If for p ≠ q ≠ 0, the function \(\begin{array}{l} f\left(x\right)=\frac{\sqrt[7]{p\left(729+x\right)}-3}{\sqrt[3]{729+qx}-9}\end{array} \)
is continuous at x = 0, then
\(\begin{array}{l}\left(A\right) 7pq~f\left(0\right) – 1 = 0\end{array} \)
\(\begin{array}{l}\left(B\right) 63q f\left(0\right) – p^2 = 0\end{array} \)
\(\begin{array}{l}\left(C\right) 21qf\left(0\right) – p^2 = 0\end{array} \)
\(\begin{array}{l}\left(D\right) 7pq f\left(0\right) – 9 = 0\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} f\left(x\right)=\frac{\sqrt[7]{p\left(729+x\right)}-3}{\sqrt[3]{729+qx}-9}\end{array} \)
\(\begin{array}{l}\text{for continuity at}\ x = 0,\displaystyle \lim_{x \to 0}f\left(x\right)=f\left(0\right)\end{array} \)
Now,
\(\begin{array}{l}\therefore \displaystyle \lim_{x \to 0}f\left(x\right)=\displaystyle \lim_{x \to 0}\frac{\sqrt[7]{p\left(729+x\right)}-3}{\sqrt[3]{729+qx}-9}\end{array} \)
\(\begin{array}{l}\Rightarrow p = 3 \left(\text{To make indeterminant form}\right)\end{array} \)
So, \(\begin{array}{l} \displaystyle \lim_{x \to 0}f\left(x\right)=\displaystyle \lim_{x \to 0}\frac{\left(3^7+3x\right)^\frac{1}{7}-3}{\left(729+qx\right)^\frac{1}{3}-9}\end{array} \)
\(\begin{array}{l} =\displaystyle \lim_{x \to 0}\frac{3\left[\left(1+\frac{x}{3^6}\right)^\frac{1}{7}-1\right]}{9\left[\left(1+\frac{q}{729}x\right)^\frac{1}{3}-1\right]}=\frac{1}{3}\cdot\frac{\frac{1}{7}\cdot\frac{1}{3^6}}{\frac{1}{3}\cdot\frac{q}{729}}\end{array} \)
\(\begin{array}{l} \therefore\ f\left(0\right)=\frac{1}{7q}\end{array} \)
∴ Option (B) is correct
6. Let \(\begin{array}{l} f\left(x\right)=2+\left|x\right|-\left|x-1\right|+\left|x+1\right| ,x\in R.\end{array} \)
\(\begin{array}{l}\text{Consider}\left(S1\right) :f’\left(-\frac{3}{2}\right)+f’\left(-\frac{1}{2}\right)+f’\left(\frac{1}{2}\right)+f’\left(\frac{3}{2}\right)=2\end{array} \)
\(\begin{array}{l} \left(S2\right):\displaystyle\int\limits_{-2}^2f\left(x\right)dx=12\end{array} \)
Then,
(A) Both (S1) and (S2) are correct
(B) Both (S1) and (S2) are wrong
(C) Only (S1) is correct
(D) Only (S2) is correct
Answer (D)
Sol.
\(\begin{array}{l} f\left(x\right)=2+\left|x\right|-\left|x-1\right|+\left|x+1\right|, x\in R\end{array} \)
\(\begin{array}{l} \therefore\ f\left(x\right)=\left\{\begin{matrix}-x & , & x<-1 \\x+2 & , & -1\leq x<0 \\3x+2 & , & 0\leq x <1 \\x+4 & , & x\geq 1 \\\end{matrix}\right.\end{array} \)
\(\begin{array}{l} \therefore\ f’\left(-\frac{3}{2}\right)+f’\left(-\frac{1}{2}\right)+f’\left(\frac{1}{2}\right)+f’\left(\frac{3}{2}\right)=-1+1+3+1=4\end{array} \)
\(\begin{array}{l} \text{and} \displaystyle\int\limits_{-2}^2f\left(x\right)dx=\displaystyle\int\limits_{-2}^{-1}f\left(x\right)dx+\displaystyle\int\limits_{-1}^0f\left(x\right)dx+\displaystyle\int\limits_{0}^1f\left(x\right)dx+\displaystyle\int\limits_{1}^2f\left(x\right)dx\end{array} \)
\(\begin{array}{l} =\left[-\frac{x^2}{2}\right]_{-2}^{-1}+\left[\frac{\left(x+2\right)^2}{2}\right]_{-1}^0+\left[\frac{\left(3x+2\right)^2}{6}\right]_{0}^1+\left[\frac{\left(x+4\right)^2}{2}\right]_{1}^2\end{array} \)
\(\begin{array}{l} =\frac{3}{2}+\frac{3}{2}+\frac{7}{2}+\frac{11}{2}=\frac{24}{2}=12 \end{array} \)
∴ Only (S2) is correct
7. Let the sum of an infinite G.P., whose first term is a and the common ratio is r, be 5. Let the sum of its first five terms be 98/25. Then the sum of the first 21 terms of an AP, whose first term is 10ar, nth term is an and the common difference is 10ar2, is equal to
(A) 21 a11
(B) 22 a11
(C) 15 a16
(D) 14 a16
Answer (A)
Sol. Let first term of G.P. be a and common ratio is r
\(\begin{array}{l} \text{Then,} \frac{a}{1-r}=5\cdots\left(i\right)\end{array} \)
\(\begin{array}{l} a\frac{\left(r^5-1\right)}{\left(r-1\right)}=\frac{98}{25}\Rightarrow 1-r^5 = \frac{98}{125} \end{array} \)
\(\begin{array}{l} \therefore\ r^5=\frac{27}{125}, r=\left(\frac{3}{5}\right)^\frac{3}{5}\end{array} \)
\(\begin{array}{l}\therefore\text{Then,} S_{21}=\frac{21}{2}\left[2\times 10\text{ar}+20\times10\text{ar}^2\right] \end{array} \)
\(\begin{array}{l} =21\left[10\text{ar}+10\cdot10\text{ar}^2\right]= ^{21}a_{11}\end{array} \)
8. The area of the region enclosed by \(\begin{array}{l}y\leq 4x^2, x^2\leq 9y\text{ and }y\leq 4,\end{array} \)
is equal to
\(\begin{array}{l} (\text{A})\ \frac{40}{3}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{56}{3}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{112}{3}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{80}{3}\end{array} \)
Answer (D)
Sol.
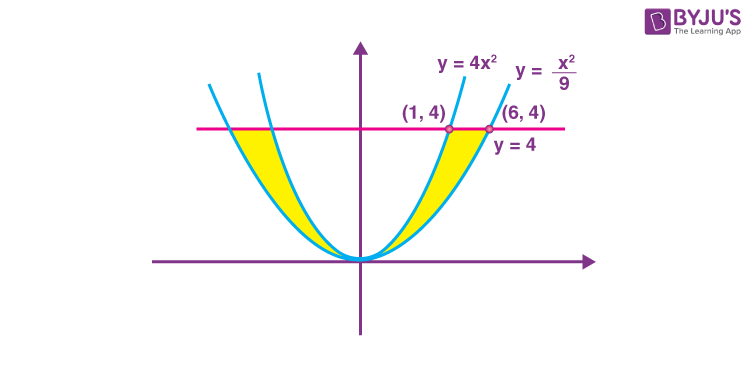
\(\begin{array}{l} y\leq 4x^2, x^2\leq 9y, y\leq 4 \end{array} \)
So, required area
\(\begin{array}{l} A=2\int_0^4\left(3\sqrt{y}-\frac{1}{2}\sqrt{y}\right)dy\end{array} \)
\(\begin{array}{l} =2\cdot\frac{5}{2}~~~~\left[\frac{2}{3}y^\frac{3}{2}\right]_0^4\end{array} \)
\(\begin{array}{l} =\frac{10}{3}~~~~\left[4^\frac{3}{2}-0\right]=\frac{80}{3}\end{array} \)
9. \(\begin{array}{l} \displaystyle\int\limits_0^2\left(\left|2x^2-3x\right|+\left[x-\frac{1}{2}\right]\right)dx, \end{array} \)
where [t] is the greatest integer function, is equal to
\(\begin{array}{l} (\text{A})\ \frac{7}{6}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{19}{12}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{31}{12}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{3}{2}\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} \displaystyle\int\limits_0^2\left|2x^2-3x\right|dx+\displaystyle\int\limits_0^2\left[x-\frac{1}{2}\right]dx\end{array} \)
\(\begin{array}{l} =\displaystyle\int\limits_0^{3/2}\left(3x-2x^2\right)dx+\displaystyle\int\limits_{3/2}^{2}\left(2x^2-3x\right)dx+\displaystyle\int\limits_0^{1/2}-1dx+\displaystyle\int\limits_{1/2}^{3/2}0dx+\displaystyle\int\limits_{3/2}^{2}1dx\end{array} \)
\(\begin{array}{l} \left.=\left(\frac{3x^2}{2}-\frac{2x^3}{3}\right) \right|_0^{3/2}+\left.\left(\frac{2x^3}{3}-\frac{3x^2}{2}\right) \right|_{3/2}^2-\frac{1}{2}+\frac{1}{2}\end{array} \)
\(\begin{array}{l} =\left(\frac{27}{8}-\frac{27}{12}\right) +\left(\frac{16}{3}-6-\frac{27}{12}+\frac{27}{8}\right)\end{array} \)
\(\begin{array}{l} =\frac{19}{12}\end{array} \)
10. Consider a curve y = y(x) in the first quadrant as shown in the figure. Let the area A1 is twice the area A2. Then the normal to the curve perpendicular to the line 2x – 12y = 15 does NOT pass through the point.
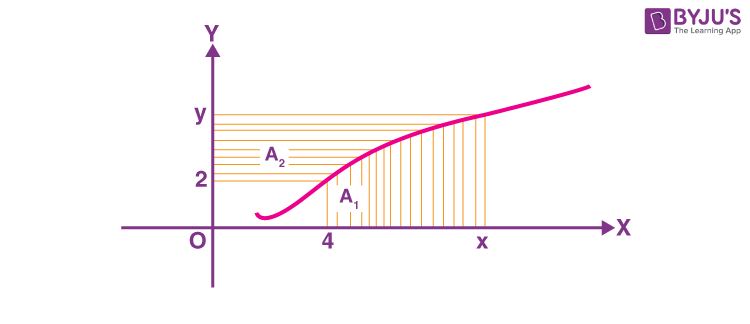
\(\begin{array}{l}\left(A\right) \left(6, 21\right)\\\left(B\right) \left(8, 9\right)\\ \left(C\right) \left(10, -4\right)\\ \left(D\right) \left(12, -15\right)\end{array} \)
Answer (C)
Sol.
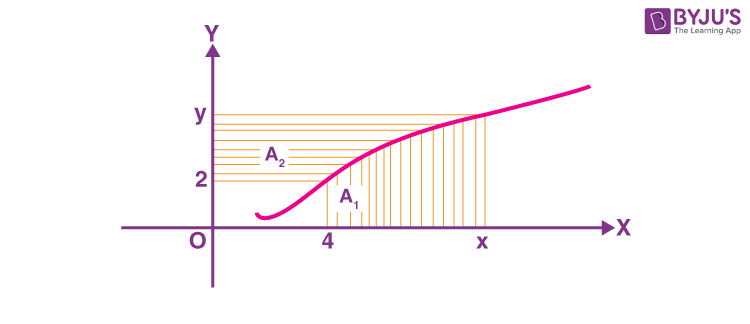
\(\begin{array}{l} A_1+A_2=xy-8~\&~A_1=2A_2 \end{array} \)
\(\begin{array}{l} A_1+\frac{A_1}{2}=xy-8\end{array} \)
\(\begin{array}{l} A_1=\frac{2}{3}\left(xy-8\right)\end{array} \)
\(\begin{array}{l} \displaystyle\int\limits_4^xf\left(x\right)dx=\frac{2}{3}\left(xf\left(x\right)-8\right)\end{array} \)
Differentiate w.r.t.x
\(\begin{array}{l} f\left(x\right)=\frac{2}{3}\left\{xf’\left(x\right)+f\left(x\right) \right\} \end{array} \)
\(\begin{array}{l} \frac{2}{3}xf’\left(x\right)=\frac{1}{3}f\left(x\right) \end{array} \)
\(\begin{array}{l} 2\int\frac{f’\left(x\right)}{f\left(x\right)}dx=\int\frac{dx}{x}\end{array} \)
\(\begin{array}{l}2lnf(x) = lnx + lnc\\f^2(x) = cx\end{array} \)
Which passes through (4, 2)
\(\begin{array}{l}4 = c \times 4 \Rightarrow c = 1\end{array} \)
Equation of required curve y2 = x
Equation of normal having slope (–6) is
\(\begin{array}{l}y =-6x-2\left(\frac{1}{4}\right)\left(-6\right)-\frac{1}{4}\left(-6\right)^3 \\y = -6x + 57\end{array} \)
Which does not pass through (10, –4)
11. The equations of the sides AB, BC and CA of a triangle ABC are 2x + y = 0, x + py = 39 and x – y = 3, respectively and P(2, 3) is its circumcentre. Then which of the following is NOT true?
\(\begin{array}{l}\left(A\right) \left(AC\right)^2 = 9p\\ \left(B\right) \left(AC\right)^2 + p^2 = 136\\\left(C\right) 32 < area\left(\triangle ABC\right) < 36\\ \left(D\right)34 < area\left(\triangle ABC\right) < 38\end{array} \)
Answer (D)
Sol. Intersection of 2x + y = 0 and x – y = 3 :A(1, –2)
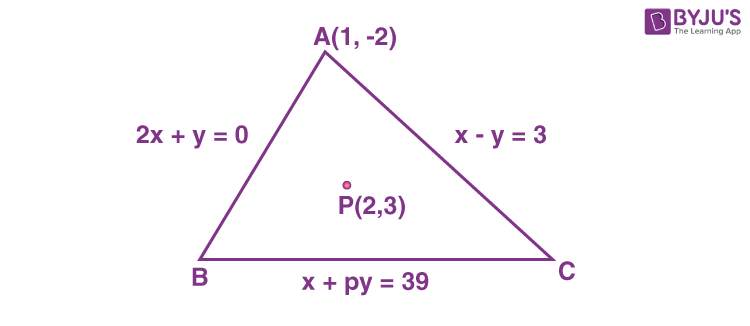
Equation of perpendicular bisector of AB is
x – 2y = –4
Equation of perpendicular bisector of AC is
x + y = 5
Point B is the image of A in line x – 2y + 4 = 0
which can be obtained as
\(\begin{array}{l} B\left(\frac{-13}{5},\frac{26}{5}\right)\end{array} \)
Similarly vertex C : (7, 4)
Equation of line BC : x + 8y = 39
So, p = 8
\(\begin{array}{l} AC=\sqrt{\left(7-1\right)^2+\left(4+2\right)^2} =6\sqrt{2}\end{array} \)
Area of triangle ABC = 32.4
12. A circle C1 passes through the origin O and has diameter 4 on the positive x-axis. The line y = 2x gives a chord OA of circle C1. Let C2 be the circle with OA as a diameter. If the tangent to C2 at the point A meets the x-axis at P and y-axis at Q, then QA :AP is equal to
(A) 1 : 4
(B) 1 : 5
(C) 2 : 5
(D) 1 : 3
Answer (A)
Sol. Equation of C1
x2 + y2 – 4x = 0
Intersection with
y = 2x
\(\begin{array}{l} x^2+4x^2-4x=0\end{array} \)
\(\begin{array}{l} \begin{matrix}5x^2-4x=0\Rightarrow & x=0,\frac{4}{5} \\ & y=0,\frac{8}{5} \\\end{matrix}\end{array} \)
\(\begin{array}{l} A:\left(\frac{4}{5},\frac{8}{5}\right)\end{array} \)
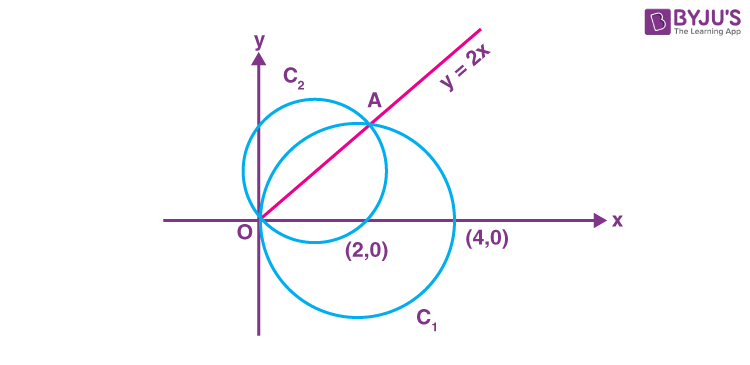
\(\begin{array}{l}\text{Tangent of} ~C_2~ at A\left(\frac{4}{5},\frac{8}{5}\right) \end{array} \)
\(\begin{array}{l} x+2y=4\Rightarrow P:\left(4,0\right), Q:\left(0,2\right) \end{array} \)
\(\begin{array}{l} QA:AP=1:4 \end{array} \)
13. If the length of the latus rectum of a parabola, whose focus is (a, a) and the tangent at its vertex is x + y = a, is 16, then |a| is equal to :
\(\begin{array}{l} (\text{A})\ 2\sqrt{2}\end{array} \)
\(\begin{array}{l} (\text{B})\ 2\sqrt{3}\end{array} \)
\(\begin{array}{l} (\text{C})\ 4\sqrt{2}\end{array} \)
\(\begin{array}{l} (\text{D})\ 4\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l}\text{Equation of tangent at vertex :} L\equiv x+y-a=0\end{array} \)
\(\begin{array}{l} \text{Focus}:F\equiv\left(a, a\right)\\\text{Perpendicular distance of L from F}\end{array} \)
\(\begin{array}{l} =\left|\frac{a+a-a}{\sqrt{2}}\right|=\left|\frac{a}{\sqrt{2}}\right| \end{array} \)
\(\begin{array}{l}\text{Length of latus rectum} =4\left|\frac{a}{\sqrt{2}}\right| \end{array} \)
\(\begin{array}{l} \text{Given} ~4\cdot\left|\frac{a}{\sqrt{2}}\right|=16\end{array} \)
\(\begin{array}{l} \Rightarrow\ \left|a\right|=4\sqrt{2}\end{array} \)
14. If the length of the perpendicular drawn from the point P(a, 4, 2), a> 0 on the line \(\begin{array}{l} \frac{x+1}{2}=\frac{y-3}{3} =\frac{z-1}{-1}\text{is }2\sqrt{6}\ \text{units}\ \text{and}\ Q\left(\alpha_1,\alpha_2,\alpha_3\right)\end{array} \)
is the image of the point P in this line, then \(\begin{array}{l} a+\sum_{i=1}^{3}\alpha_i \end{array} \)
is equal to :
(A) 7
(B) 8
(C) 12
(D) 14
Answer (B)
Sol. ∵ PR is perpendicular to given line, so
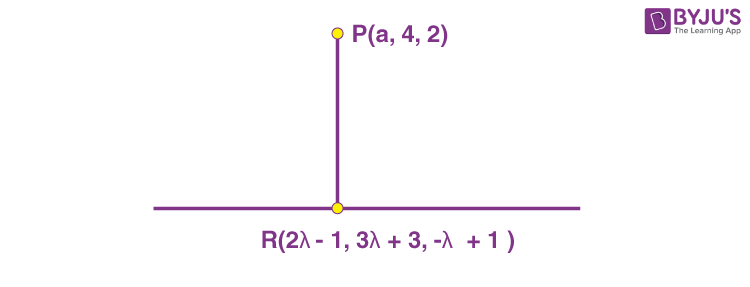
\(\begin{array}{l} 2\left(2\lambda-1-a\right)+3\left(3\lambda-1\right)-1\left(-\lambda-1\right)=0\end{array} \)
\(\begin{array}{l} \Rightarrow\ a=7\lambda-2\end{array} \)
\(\begin{array}{l}\text{ Now} \\\because\ PR=2\sqrt{6}\end{array} \)
\(\begin{array}{l} \Rightarrow\ \left(-5\lambda+1\right)^2+\left(3\lambda-1\right)^2+\left(\lambda+1\right)^2=24\end{array} \)
\(\begin{array}{l} \Rightarrow 5\lambda^2-2\lambda-3=0\Rightarrow \lambda=1\text{ or }-\frac{3}{5}\end{array} \)
\(\begin{array}{l} \because\ a>0\text{ so }\lambda=1\text{ and }a=5 \end{array} \)
\(\begin{array}{l}\text{ Now } \sum_{i=1}^{3}\alpha_i=2\left(\text{ Sum of co-ordinate of }R\right) -\left(\text{Sum of coordinates of }P\right) \end{array} \)
\(\begin{array}{l} = 2\left(7\right) – 11 = 3\end{array} \)
\(\begin{array}{l} a+\sum_{i=1}^{3}\alpha_i=5+3=8\end{array} \)
15. If the line of intersection of the planes ax + by = 3 and ax + by + cz = 0, a> 0 makes an angle 30° with the plane y – z + 2 = 0, then the direction cosines of the line are :
\(\begin{array}{l} (\text{A})\ \frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}},0\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}},0\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{1}{\sqrt{5}},-\frac{2}{\sqrt{5}},0\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{1}{2},-\frac{\sqrt{3}}{2},0\end{array} \)
Answer (B)
Sol.
\(\begin{array}{l} P_1 :ax + by + 0z = 3, \text{normal vector :} \overrightarrow{n}1=\left(a,b,0\right) \end{array} \)
\(\begin{array}{l}P_2 :ax + by + cz= 0, \text{normal vector :} \overrightarrow{n}_2=\left(a,b,c\right) \end{array} \)
\(\begin{array}{l} \text{Vector parallel to the line of intersection =} \overrightarrow{n}_1\times \overrightarrow{n}_2\\\overrightarrow{n}_1\times\overrightarrow{n}_2=\left(bc,-ac,0\right)\end{array} \)
\(\begin{array}{l}\text{Vector normal to}~0.x+y-z+2=0~ is~ \overrightarrow{n}_3=\left(0,1, -1\right)\end{array} \)
\(\begin{array}{l}\text{Angle between line and plane is} ~30^\circ \Rightarrow\ \left|\frac{0-ac+0}{\sqrt{b^2c^2+c^2a^2}\sqrt{2}}\right|=\frac{1}{2} \end{array} \)
\(\begin{array}{l} \Rightarrow\ a^2=b^2\end{array} \)
\(\begin{array}{l} \text{ Hence,}\overrightarrow{n}_1\times\overrightarrow{n}_2=\left(ac,-ac,0\right)\end{array} \)
\(\begin{array}{l} \text{ Direction ratios =} \left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}},0\right) \end{array} \)
16. Let X have a binomial distribution B(n, p) such that the sum and the product of the mean and variance of X are 24 and 128 respectively. If \(\begin{array}{l}P\left(X>n – 3\right) = \frac{k}{2^n},\end{array} \)
then k is equal to :
(A) 528
(B) 529
(C) 629
(D) 630
Answer (B)
Sol. Mean = np = 16
Variance = npq = 8
\(\begin{array}{l} \Rightarrow\ q = p = \frac{1}{2}~\text{and}~ n = 32\\P\left(x>n – 3\right) = p\left(x = n – 2\right) + p\left(x = n – 1\right) + p\left(x = n\right)\end{array} \)
\(\begin{array}{l} =\left(^{32}C_2+^{32}C_1+^{32}C_0\right)\cdot\frac{1}{2^n}\end{array} \)
\(\begin{array}{l} =\frac{529}{2^n} \end{array} \)
17. A six faced die is biased such that
3 × P (a prime number) = 6 × P (a composite number) = 2 × P (1).
Let X be a random variable that counts the number of times one gets a perfect square on some throws of this die. If the die is thrown twice, then the mean of X is :
\(\begin{array}{l} (\text{A})\ \frac{3}{11}\end{array} \)
\(\begin{array}{l} (\text{B})\ \frac{5}{11}\end{array} \)
\(\begin{array}{l} (\text{C})\ \frac{7}{11}\end{array} \)
\(\begin{array}{l} (\text{D})\ \frac{8}{11}\end{array} \)
Answer (D)
Sol. Let P(a prime number) = α
P(a composite number) = β
and P(1) = γ
\(\begin{array}{l}\because 3\alpha = 6\beta = 2\gamma = k (say)\\~\text{and}~ 3\alpha + 2\beta + \gamma = 1\end{array} \)
\(\begin{array}{l} \Rightarrow\ k+\frac{k}{3}+\frac{k}{2}=1\Rightarrow\ k=\frac{6}{11}\end{array} \)
Mean = np where n = 2
and p = probability of getting perfect square
\(\begin{array}{l} =P\left(1\right)+P\left(4\right)=\frac{k}{2}+\frac{k}{6}=\frac{4}{11}\end{array} \)
\(\begin{array}{l} \text{ So, mean =} 2\cdot\left(\frac{4}{11}\right)=\frac{8}{11}\end{array} \)
18. The angle of elevation of the top P of a vertical tower PQ of height 10 from a point A on the horizontal ground is 45°, Let R be a point on AQ and from a point B, vertically above R, the angle of elevation of P is 60°. If \(\begin{array}{l}\angle BAQ = 30^\circ\end{array} \)
, AB = d and the area of the trapezium PQRB is α, then the ordered pair (d, α) is :
\(\begin{array}{l} (\text{A})\ \left(10\left(\sqrt{3}-1\right),25\right) \end{array} \)
\(\begin{array}{l} (\text{B})\ \left(10\left(\sqrt{3}-1\right),\frac{25}{2}\right) \end{array} \)
\(\begin{array}{l} (\text{C})\ \left(10\left(\sqrt{3}+1\right),25\right) \end{array} \)
\(\begin{array}{l} (\text{D})\ \left(10\left(\sqrt{3}+1\right),\frac{25}{2}\right) \end{array} \)
Answer (A)
Sol. Let BR = x
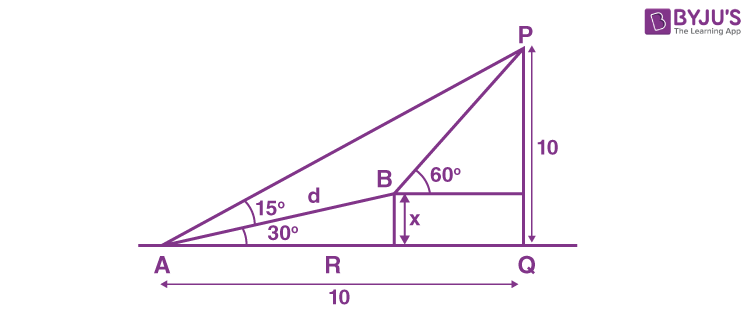
\(\begin{array}{l} \frac{x}{d}=\frac{1}{2}\Rightarrow x=\frac{d}{2}\end{array} \)
\(\begin{array}{l} \frac{10-x}{10-x\sqrt{3}}=\sqrt{3}\Rightarrow 10-x=10\sqrt{3}-3x \end{array} \)
\(\begin{array}{l} 2x=10\left(\sqrt{3}-1\right) \end{array} \)
\(\begin{array}{l} x=5\left(\sqrt{3}-1\right) \end{array} \)
\(\begin{array}{l} d=2x=10\left(\sqrt{3}-1\right)\end{array} \)
\(\begin{array}{l} \alpha=\frac{1}{2}\left(x+10\right)\left(10-x\sqrt{3}\right)=\text{Area}\left(PQRB\right)\end{array} \)
\(\begin{array}{l} =\frac{1}{2}\left(5\sqrt{3}-5+10\right)\left(10-5\sqrt{3}\left(\sqrt{3}-1\right)\right)\end{array} \)
\(\begin{array}{l} =\frac{1}{2}\left(5\sqrt{3}+5\right)\left(10-15+5\sqrt{3}\right)=\frac{1}{2}\left(75-25\right)=25\end{array} \)
19. \(\begin{array}{l} \text{ Let } S=\left\{0\in\left(0,\frac{\pi}{2}\right):\sum_{m=1}^{9}\sec\left(\theta+\left(m-1\right)\frac{\pi}{6}\right)\sec\left(\theta+\frac{m\pi}{6}\right)=-\frac{8}{\sqrt{3}} \right\} \end{array} \)
Then
\(\begin{array}{l} (\text{A})\ S=\left\{\frac{\pi}{12}\right\}\end{array} \)
\(\begin{array}{l} (\text{B})\ S=\left\{\frac{2\pi}{3}\right\}\end{array} \)
\(\begin{array}{l} (\text{C})\ \sum_{\theta\in S}\theta= \frac{\pi}{2}\end{array} \)
\(\begin{array}{l} (\text{D})\ \sum_{\theta\in S}\theta= \frac{3\pi}{4}\end{array} \)
Answer (C)
Sol.
\(\begin{array}{l} S=\left\{0\in\left(0,\frac{\pi}{2}\right):\sum_{m=1}^{9}\sec\left(\theta+\left(m-1\right)\frac{\pi}{6}\right)\sec\left(\theta+\frac{m\pi}{6}\right)=-\frac{8}{\sqrt{3}}\right\}\end{array} \)
\(\begin{array}{l} \sum_{m=1}^{9}\frac{1}{\cos\left(\theta+\left(m-1\right)\frac{\pi}{6}\right)}\cos\left(\theta+m\frac{\pi}{6}\right)\end{array} \)
\(\begin{array}{l} \frac{1}{\sin\left(\frac{\pi}{6}\right)}\sum_{m=1}^{9}\frac{\sin\left[\left(\theta+\frac{m\pi}{6}\right)-\left(\theta+\left(m-1\right)\frac{\pi}{6}\right)\right]}{\cos\left(\theta+\left(m-1\right)\frac{\pi}{6}\right)\cos\left(\theta+m\frac{\pi}{6}\right)}\end{array} \)
\(\begin{array}{l} =2\sum_{m=1}^{9}\left[\tan\left(\theta+\frac{m\pi}{6}\right)-\tan\left(\theta+\left(m-1\right)\frac{\pi}{6}\right)\right]\end{array} \)
\(\begin{array}{l} \text{ Now,} m=1~~~2\left[\tan\left(\theta+\frac{\pi}{6}\right)-\tan\left(\theta\right)\right]\end{array} \)
\(\begin{array}{l} \begin{matrix} m=2&2\left[\tan\left(\theta+\frac{2\pi}{6}\right)-\tan\left(\theta+\frac{\pi}{6}\right)\right] \\ .& \\. & \\. & \\m=9 & 2\left[\tan\left(\theta+\frac{9\pi}{6}\right)-\tan\left(\theta+8\frac{\pi}{6}\right)\right] \\\end{matrix} \end{array} \)
\(\begin{array}{l} \therefore\ =2\left[\tan\left(\theta+\frac{3\pi}{2}\right)-\tan\theta\right]=\frac{-8}{\sqrt{3}}\end{array} \)
\(\begin{array}{l} =-2\left[\cot\theta+\tan\theta\right]=\frac{-8}{\sqrt{3}} \end{array} \)
\(\begin{array}{l} =-\frac{2\times2}{2\sin\theta\cos\theta}=\frac{-8}{\sqrt{3}}\end{array} \)
\(\begin{array}{l} =\frac{1}{\sin2\theta}=\frac{2}{\sqrt{3}} \end{array} \)
\(\begin{array}{l} \Rightarrow\ \sin 2\theta=\frac{\sqrt{3}}{2} \end{array} \)
\(\begin{array}{l} 2\theta=\frac{\pi}{3}~~~2\theta=\frac{2\pi}{3} \end{array} \)
\(\begin{array}{l} \theta=\frac{\pi}{6}~~~\theta=\frac{\pi}{3}\end{array} \)
\(\begin{array}{l} \sum \theta_i=\frac{\pi}{6}+\frac{\pi}{3}=\frac{\pi}{2}\end{array} \)
20. If the truth value of the statement \(\begin{array}{l}\left(P\wedge\left(\sim R\right)\right)\rightarrow\left(\left(\sim R\right)\wedge Q\right)\end{array} \)
is F, then the truth value of which of the following is F?
\(\begin{array}{l}\left(A\right) P\vee Q ~\rightarrow ~\sim R\end{array} \)
\(\begin{array}{l}\left(B\right) R\vee Q ~\rightarrow ~\sim P\end{array} \)
\(\begin{array}{l}\left(C\right) \sim \left(P\vee Q \right)~\rightarrow ~\sim R\end{array} \)
\(\begin{array}{l}\left(D\right) \sim \left(R\vee Q \right)~\rightarrow ~\sim P\end{array} \)
Answer (D)
Sol.
\(\begin{array}{l} \underset{X}{\underbrace{P\wedge \left(\sim R\right)} }\rightarrow \underset{Y}{\underbrace{\left(\left(\sim R\right)\wedge Q\right)}}=\text{False}\end{array} \)
X→Y = False
| X |
Y |
X →Y |
| F |
F |
T |
| T |
T |
T |
| F |
T |
T |
| T |
F |
F |
\(\begin{array}{l}P\wedge \sim R = T \text{and} (\sim R ) \wedge Q = F \end{array} \)
\(\begin{array}{l}\Rightarrow P = T\\\sim R = T \Rightarrow R = F\end{array} \)
\(\begin{array}{l}\Rightarrow P = T, Q = F ~\text{and }R = F\\ T \wedge Q = F\end{array} \)
\(\begin{array}{l}\Rightarrow Q = F\\ \text{Now} \sim(R\vee Q) \rightarrow \sim P\end{array} \)
\(\begin{array}{l}\sim \left(F \vee F\right) \rightarrow F\\ F \rightarrow F = False\end{array} \)
SECTION – B
Numerical Value Type Questions: This section contains 10 questions. In Section B, attempt any five questions out of 10. The answer to each question is a NUMERICAL VALUE. For each question, enter the correct numerical value (in decimal notation, truncated/rounded-off to the second decimal place; e.g. 06.25, 07.00, –00.33, –00.30, 30.27, –27.30) using the mouse and the on-screen virtual numeric keypad in the place designated to enter the answer.
1. \(\begin{array}{l} \text{Consider a matrix}~A=\begin{bmatrix}\alpha & \beta & \gamma \\\alpha^2 & \beta^2 & \gamma^2 \\\beta+\gamma & \gamma+\alpha & \alpha+\beta \\\end{bmatrix}\end{array} \)
where α, β, γ are three distinct natural numbers.
\(\begin{array}{l}\text{If} \frac{\text{det(adj(adj(adj(adj A))))}}{\left(\alpha-\beta\right)^{16}\left(\beta-\gamma\right)^{16}\left(\gamma-\alpha\right)^{16}}=2^{32}\times3^{16},\end{array} \)
then the number of such 3-tuples (α, β, γ) is _________.
Answer (42)
Sol.
\(\begin{array}{l} \text{det}\left(A\right)=\begin{vmatrix}\alpha & \beta & \gamma \\\alpha^2 & \beta^2 & \gamma^2 \\\beta+\gamma & \gamma+\alpha & \alpha+\beta \\\end{vmatrix}\end{array} \)
\(\begin{array}{l} R_3 \rightarrow R_3 + R_1\end{array} \)
\(\begin{array}{l} \Rightarrow \left(\alpha+\beta+\gamma\right)\begin{vmatrix}\alpha & \beta & \gamma \\\alpha^2 & \beta^2 & \gamma^2 \\1 & 1 & 1 \\\end{vmatrix}\end{array} \)
\(\begin{array}{l}\therefore det \left(A\right) = \left(\alpha + \beta + \gamma\right) \left(\alpha – \beta\right) \left(\beta – \gamma\right) \left(\gamma – \alpha\right)\end{array} \)
Also, det (adj (adj (adj (adj (A)))))
\(\begin{array}{l} =\left(\text{det}\left(A\right)\right)^{2^4}=\left(\text{det}\left(A\right)\right)^{16}\end{array} \)
\(\begin{array}{l} \therefore\ \frac{\left(\alpha+\beta+\gamma\right)^{16}\left(\alpha-\beta\right)^{16}\left(\beta-\gamma\right)^{16}\left(\gamma-\alpha\right)^{16}}{\left(\alpha-\beta\right)^{16}\left(\beta-\gamma\right)^{16}\left(\gamma-\alpha\right)^{16}}=\left(4.3\right)^{16}\end{array} \)
\(\begin{array}{l}\Rightarrow \alpha + \beta + \gamma = 12 \end{array} \)
\(\begin{array}{l}\Rightarrow \left(\alpha, \beta, \gamma\right) \text{distinct natural triplets}\end{array} \)
\(\begin{array}{l}= ^{11}C_2 – 1 – ^3C_2 \left(4\right) = 55 – 1 – 12\\ = 42 \end{array} \)
2. The number of functions f, from the set \(\begin{array}{l}A = \{x \in N :x^2 – 10x + 9 \le 0\}\ \text{to the set}\ B = \{n^2 : n \in N\} \end{array} \)
such that \(\begin{array}{l}f\left(x\right) \le \left(x – 3\right)^2 + 1,\ \text{for every}\ x \in A,\end{array} \)
is _________.
Answer (1440)
Sol.
\(\begin{array}{l} A=\left\{x\in N,~~~x^2-10x+9\leq 0\right\} \end{array} \)
\(\begin{array}{l} =\left\{1,2,3,\cdots,9\right\}\end{array} \)
\(\begin{array}{l} B=\left\{1,4,9,16,\cdots\right\}\end{array} \)
\(\begin{array}{l} f\left(x\right)\leq\left(x-3\right)^2+1 \end{array} \)
\(\begin{array}{l} f\left(1\right)\leq5,\ f\left(2\right)\leq 2,\cdots f\left(9\right)\leq 37\end{array} \)
x = 1 has 2 choices
x = 2 has 1 choice
x = 3 has 1 choice
x = 4 has 1 choice
x = 5 has 2 choices
x = 6 has 3 choices
x = 7 has 4 choices
x = 8 has 5 choices
x = 9 has 6 choices
∴ Total functions = 2 × 1 × 1 × 1 × 2 × 3 × 4 × 5 × 6 = 1440
3. Let for the 9th term in the binomial expansion of (3 + 6x)n, in the increasing powers of 6x, to be the greatest for x = 3/2, the least value of n is n0. If k is the ratio of the coefficient of x6 to the coefficient of x3, then k + n0 is equal to :
Answer (24)
Sol.
\(\begin{array}{l}\left(3 + 6x\right)^n = 3^n\left(1 + 2x\right)^n\end{array} \)
If T9 is numerically greatest term
\(\begin{array}{l}\therefore T_8 \le T_9 \geq T_{10}\end{array} \)
\(\begin{array}{l}nC_7 3^{n–7} \left(6x\right)^7\le nC_8 3^{n–8} \left(6x\right)^8 \geq nC_9 3^{n–9} \left(6x\right)^9\end{array} \)
\(\begin{array}{l} \Rightarrow\ \frac{n!}{\left(n-7\right)!7!}9\leq \frac{n!}{\left(n-8\right)!8!}3\cdot\left(6x\right)\geq\frac{n!}{\left(n-9\right)!9!}\left(6x\right)^2\end{array} \)
\(\begin{array}{l} \Rightarrow\ \underbrace{\frac{9}{\left(n-7\right)\left(n-8\right)}}\leq\underbrace{\frac{18\left(\frac{3}{2}\right)}{\left(n-8\right)8}}\geq \frac{36}{9.8}\frac{9}{4}\end{array} \)
\(\begin{array}{l}72 \le 27\left(n – 7\right) ~\text{and}~ 27 \geq 9\left(n – 8\right)\end{array} \)
\(\begin{array}{l} \frac{29}{3}\leq n\ \text{and}\ n \le 11\end{array} \)
\(\begin{array}{l}\therefore n_0 = 10\end{array} \)
\(\begin{array}{l}\text{For} \left(3 + 6x\right)^{10}\end{array} \)
\(\begin{array}{l}T_{r + 1} = ^{10}C_r ~~~~~~~~~~~~3^{10 – r} \left(6x\right)^r\end{array} \)
\(\begin{array}{l}\text{For coeff. of }x^6\\ r = 6 \Rightarrow ^{10}C_63^4.6^6\end{array} \)
\(\begin{array}{l}\text{For coeff. of} x^3\\ r = 3 \Rightarrow ^{10}C_33^7.6^3\end{array} \)
\(\begin{array}{l} \therefore\ k=\frac{^{10}C_6}{^{10}C_3}\cdot\frac{3^4\cdot 6^6}{3^7\cdot 6^3}=\frac{10!7!3!}{6!4!10!}\cdot 8 \end{array} \)
\(\begin{array}{l}\Rightarrow k = 14\\ \therefore k + n_0 = 24\end{array} \)
4. \(\begin{array}{l} \frac{2^3-1^3}{1\times7}+\frac{4^3-3^3+2^2-1^3}{2\times 11}+\frac{6^3-5^3+4^3-3^3+2^3-1^3}{3\times 15}+\cdots+\frac{30^3-29^3+28^3-27^3+\cdots+2^3-1^3}{15\times63}\end{array} \)
is equal to _______.
Answer (120)
Sol.
\(\begin{array}{l} T_n=\frac{\displaystyle\sum\limits_{k=1}^{n}\left[\left(2k\right)^3-\left(2k-1\right)^3\right]}{n\left(4n+3\right)} \end{array} \)
\(\begin{array}{l} =\frac{\displaystyle\sum\limits_{k=1}^{n}4k^2+\left(2k-1\right)^2+2k\left(2k-1\right)}{n\left(4n+3\right)}\end{array} \)
\(\begin{array}{l} =\frac{\displaystyle\sum\limits_{k=1}^{n}\left(12k^2-6k+1\right)}{n\left(4n+3\right)}\end{array} \)
\(\begin{array}{l} =\frac{2n\left(2n^2+3n+1\right)-3n^2-3n+n}{n\left(4n+3\right)} \end{array} \)
\(\begin{array}{l} =\frac{n^2\left(4n+3\right)}{n\left(4n+3\right)}=n\end{array} \)
\(\begin{array}{l} \therefore\ T_n=n \end{array} \)
\(\begin{array}{l} S_n=\displaystyle\sum\limits_{n=1}^{15}T_n=\frac{15\times16}{2}=120\end{array} \)
5. A water tank has the shape of a right circular cone with axis vertical and vertex downwards. Its semi-vertical angle is tan-1(3/4). Water is poured in it at a constant rate of 6 cubic meter per hour. The rate (in square meter per hour), at which the wet curved surface area of the tank is increasing, when the depth of water in the tank is 4 meters, is
Answer (5)
Sol.
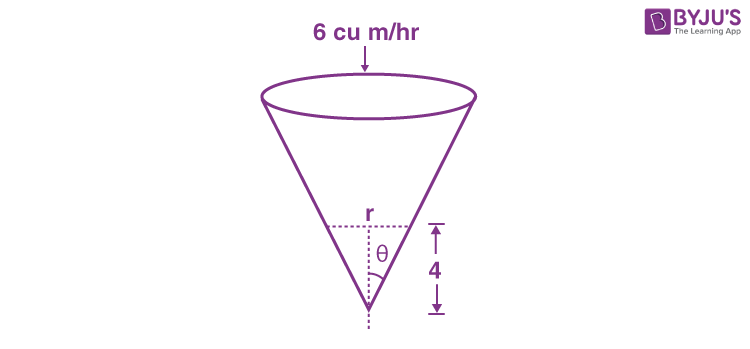
tan θ = 3/4
\(\begin{array}{l} v=\frac{1}{3}\pi r^2h\cdots\left(i\right)\end{array} \)
And
\(\begin{array}{l}\tan\theta=\frac{3}{4}=\frac{r}{h}\cdots\left(ii\right)\end{array} \)
i.e. if h = 4, r = 3
\(\begin{array}{l} v=\frac{1}{3}\pi r^2\left(\frac{4r}{3}\right) \end{array} \)
\(\begin{array}{l} \frac{dv}{dt}=\frac{4\pi}{9}3r^2\frac{dr}{dt}\Rightarrow 6=\frac{4\pi}{3}\left(9\right)\frac{dr}{dt} \end{array} \)
\(\begin{array}{l} \Rightarrow \frac{dr}{dt}=\frac{1}{2\pi}\end{array} \)
Curved area =
\(\begin{array}{l} \pi r\sqrt{r^2+h^2} \end{array} \)
\(\begin{array}{l} =\pi r\sqrt{r^2+\frac{16r^2}{9}}\end{array} \)
\(\begin{array}{l} =\frac{5}{3}\pi r^2 \end{array} \)
\(\begin{array}{l} \frac{dA}{dt}=\frac{10}{3}\pi r\frac{dr}{dt}\end{array} \)
\(\begin{array}{l} =\frac{10}{3}\pi\cdot3\cdot\frac{1}{2\pi}= 5 \end{array} \)
6. For the curve \(\begin{array}{l}C : \left(x^2 + y^2 – 3\right) + \left(x^2 – y^2 – 1\right)^5 = 0, \end{array} \)
\(\begin{array}{l}\text{the value of}\ 3y’ – y^3y”, \text{at the point}\end{array} \)
(α, α), α > 0, on C is equal to ________.
Answer (16)
Sol.
\(\begin{array}{l}\because C : \left(x^2 + y^2 – 3\right) + \left(x^2 – y^2 – 1\right)^5 = 0\end{array} \)
for point (α, α).
\(\begin{array}{l}\alpha ^2 + \alpha ^2 – 3 + (\alpha^ 2 – \alpha ^2 – 1)^5 = 0\end{array} \)
\(\begin{array}{l} \therefore\ \alpha=\sqrt{2}\end{array} \)
.
\(\begin{array}{l}\text{On differentiating} \left(x^2 + y^2 – 3\right) + \left(x^2 – y^2 – 1\right)^5 = 0 ~\text{we get}\\ x + yy’ + 5 \left(x^2 – y^2 – 1\right)^4 \left(x – yy’\right) = 0 …\left(i\right)\end{array} \)
When
\(\begin{array}{l} x=y=\sqrt{2}\end{array} \)
then \(\begin{array}{l} y’=\frac{3}{2} \end{array} \)
.
Again on differentiating eq. (i) we get :
\(\begin{array}{l}1 + \left(y’\right)^2 + yy” + 20 \left(x^2 – y^2 – 1\right) \left(2x – 2 yy’\right) \end{array} \)
\(\begin{array}{l}\left(x – y’y\right) + 5\left(x^2 – y^2 – 1\right)^4 \left(1 – y’^2 – yy”\right) = 0\end{array} \)
For
\(\begin{array}{l} x=y=\sqrt{2} \end{array} \)
and \(\begin{array}{l} y’=\frac{3}{2}\end{array} \)
we get \(\begin{array}{l} y”=-\frac{23}{4\sqrt{2}}\end{array} \)
\(\begin{array}{l}\therefore 3y’ – y^3y” =3\cdot\frac{3}{2}-\left(\sqrt{2}\right)^3\cdot\left(-\frac{23}{4\sqrt{2}}\right)\\= 16\end{array} \)
7. Let \(\begin{array}{l}f\left(x\right) = min \{\left[x – 1\right], \left[x – 2\right], …., \left[x – 10\right]\}\end{array} \)
where [t] denotes the greatest integer ≤t. Then \(\begin{array}{l} \displaystyle\int\limits_{0}^{10}f\left(x\right)dx+\displaystyle\int\limits_{0}^{10}\left(f\left(x\right)\right)^2dx+\displaystyle\int\limits_{0}^{10}\left|f\left(x\right)\right|dx\end{array} \)
is equal to ________.
Answer (385)
Sol.
\(\begin{array}{l}\because f\left(x\right) = min \{\left[x – 1\right], \left[x – 2\right], ….., [x – 10]\} = \left[x – 10\right] \end{array} \)
Also
\(\begin{array}{l}\left|f\left(x\right)\right|=\left\{\begin{matrix}-f\left(x\right), & \text{if } x\leq 10 \\f\left(x\right), & \text{if } x \geq 10 \\\end{matrix}\right.\end{array} \)
\(\begin{array}{l} \therefore\ \displaystyle\int\limits_{0}^{10}f\left(x\right)dx+\displaystyle\int\limits_{0}^{10}\left(f\left(x\right)\right)^2dx+\displaystyle\int\limits_{0}^{10}\left(-f\left(x\right)\right)dx\end{array} \)
\(\begin{array}{l} =\displaystyle\int\limits_{0}^{10}\left(f\left(x\right)\right)^2dx\end{array} \)
\(\begin{array}{l}= 10^2 + 9^2 + 8^2 + …… + 1^2\\ =\frac{10\times11\times21}{6} \\= 385\end{array} \)
8. Let f be a differential function satisfying \(\begin{array}{l} f\left(x\right)=\frac{2}{\sqrt{3}}\displaystyle\int\limits_0^{\sqrt{3}}f\left(\frac{\lambda^2x}{3}\right)d\lambda,x>0\ \text{and}\ f\left(1\right)=\sqrt{3}.\end{array} \)
If y = f(x) passes through the point (α, 6), then α is equal to _____
Answer (12)
Sol.
\(\begin{array}{l}\because\ f\left(x\right)=\frac{2}{\sqrt{3}}\displaystyle\int\limits_0^{\sqrt{3}}f\left(\frac{\lambda^2x}{3}\right)d\lambda, x>0\cdots\left(i\right)\end{array} \)
On differentiating both sides w.r.t., x, we get
\(\begin{array}{l} f’\left(x\right)=\frac{2}{\sqrt{3}}\displaystyle\int\limits_0^{\sqrt{3}}\frac{\lambda^2}{3}f’\left(\frac{\lambda^2x}{3}\right)d\lambda\end{array} \)
\(\begin{array}{l} f’\left(x\right)=\frac{1}{\sqrt{3}}\displaystyle\int\limits_0^{\sqrt{3}}\lambda\cdot\frac{2\lambda}{3}f’\left(\frac{\lambda^2x}{3}\right)d\lambda\end{array} \)
\(\begin{array}{l} \therefore \sqrt{3}f’\left(x\right)=\left[\frac{\lambda}{x}\cdot f\left(\frac{\lambda^2x}{3}\right)\right]_0^{\sqrt{3}}-\displaystyle\int\limits_0^{\sqrt{3}}\frac{1}{x}f\left(\frac{\lambda^2x}{3}\right)dx\end{array} \)
\(\begin{array}{l} \sqrt{3}xf’\left(x\right)=\sqrt{3}f\left(x\right)-\frac{\sqrt{3}}{2}f\left(x\right)\end{array} \)
\(\begin{array}{l} xf’\left(x\right)=\frac{f\left(x\right)}{2} \end{array} \)
On integrating we get :
\(\begin{array}{l} \text{In }y=\frac{1}{2}\text{ In }x+\text{ In }c\end{array} \)
\(\begin{array}{l} \because\ f\left(1\right)=\sqrt{3}\text{ then } c=\sqrt{3} \end{array} \)
\(\begin{array}{l}\therefore \left(\alpha, 6\right)\text{lies on} \end{array} \)
\(\begin{array}{l} \therefore y=\sqrt{3x}\end{array} \)
\(\begin{array}{l} \therefore\ 6=\sqrt{3\alpha}\Rightarrow \alpha = 12. \end{array} \)
9. A common tangent T to the curves \(\begin{array}{l} C_1:\frac{x^2}{4}+\frac{y^2}{9}=1 \end{array} \)
and \(\begin{array}{l} C_2:\frac{x^2}{42}-\frac{y^2}{143}=1 \end{array} \)
does not pass through the fourth quadrant. If T touches C1 at (x1, y1) and C2 at (x2, y2), then |2x1 + x2| is equal to ______.
Answer (20)
Sol. Equation of tangent to ellipse
\(\begin{array}{l} \frac{x^2}{4}+\frac{y^2}{9}=1\end{array} \)
and given slope m is : \(\begin{array}{l} y=mx+\sqrt{4m^2+9}\cdots\left(i\right) \end{array} \)
For slope m equation of tangent to hyperbola is :
\(\begin{array}{l} y=mx+\sqrt{42m^2-143}\cdots\left(ii\right) \end{array} \)
Tangents from (i) and (ii) are identical then
4m2 + 9 = 42m2 – 143
\(\begin{array}{l}\therefore m = \pm 2~~~~~~~~~~\left(+2 ~\text{is not acceptable}\right)\end{array} \)
\(\begin{array}{l}\therefore m = – 2.\end{array} \)
Hence
\(\begin{array}{l} x_1=\frac{8}{5}\end{array} \)
and \(\begin{array}{l} x_2=\frac{84}{5}\end{array} \)
\(\begin{array}{l} \therefore\ \left|2x_1+x_2\right|=\left|\frac{16}{5}+\frac{84}{5}\right|=20\end{array} \)
10. Let \(\begin{array}{l} \vec{a},\vec{b},\vec{c}\ \text{be three non-coplanar vectors such that}\end{array} \)
\(\begin{array}{l} \overrightarrow{a}\times\vec{b}=4\vec{c},\vec{b}\times\vec{c}=9\vec{a}\ \text{and}\ \vec{c}\times\vec{a}=\alpha\vec{b},\alpha>0.\end{array} \)
If \(\begin{array}{l} \left|\overrightarrow{a}\right|+\left|\overrightarrow{b}\right|+\left|\overrightarrow{c}\right|=\frac{1}{36}\end{array} \)
, then α is equal to ______.
Answer (*)
Sol. Given
\(\begin{array}{l} \overrightarrow{a}\times\overrightarrow{b}=4\cdot\overrightarrow{c}\cdots\left(i\right)\end{array} \)
\(\begin{array}{l} \overrightarrow{b}\times\overrightarrow{c}=9\cdot\overrightarrow{a}\cdots\left(ii\right)\end{array} \)
\(\begin{array}{l} \overrightarrow{c}\times\overrightarrow{a}=\alpha\cdot\overrightarrow{b}\cdots\left(iii\right)\end{array} \)
\(\begin{array}{l}\text{Taking dot products with}\ \overrightarrow{c},\overrightarrow{a},\overrightarrow{b},\ \text{we get}\end{array} \)
\(\begin{array}{l} \overrightarrow{a}\cdot\overrightarrow{b}=\overrightarrow{b}\cdot\overrightarrow{c}=\overrightarrow{c}\cdot\overrightarrow{a}=0\end{array} \)
Hence
\(\begin{array}{l} \left(i\right)\Rightarrow \left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|=4\cdot\left|\overrightarrow{c}\right|\cdots\left(iv\right)\end{array} \)
\(\begin{array}{l} \left(ii\right)\Rightarrow \left|\overrightarrow{b}\right|\cdot\left|\overrightarrow{c}\right|=9\cdot\left|\overrightarrow{a}\right|\cdots\left(v\right)\end{array} \)
\(\begin{array}{l} \left(iii\right)\Rightarrow \left|\overrightarrow{c}\right|\cdot\left|\overrightarrow{a}\right|=\alpha\cdot\left|\overrightarrow{b}\right|\cdots\left(vi\right)\end{array} \)
Multiplying (iv), (v) and (vi)
\(\begin{array}{l} \Rightarrow \left|\overrightarrow{a}\right|\cdot\left|\overrightarrow{b}\right|\cdot\left|\overrightarrow{c}\right|=36\alpha\cdots\left(vii\right)\end{array} \)
Dividing (vii) by (iv)
\(\begin{array}{l} \Rightarrow\ \left|\overrightarrow{c}\right|^2=9\alpha\Rightarrow \left|\overrightarrow{c}\right|=3\sqrt{\alpha}\cdots\left(viii\right)\end{array} \)
Dividing (vii) by (v)
\(\begin{array}{l} \Rightarrow\ \left|\vec{a}\right|^2=4\alpha\Rightarrow\left|\overrightarrow{a}\right|=2\sqrt{\alpha}\end{array} \)
Dividing (viii) by (vi)
\(\begin{array}{l} \Rightarrow\ \left|\overrightarrow{b}\right|^2=36\Rightarrow \left|\overrightarrow{b}\right|=6\end{array} \)
Now, as given,
\(\begin{array}{l} 3\sqrt{\alpha}+2\sqrt{\alpha}+6=\frac{1}{36}\Rightarrow \sqrt{\alpha}=\frac{-43}{36}\end{array} \)
JEE Main 2022 July 27th Shift 2 Paper Analysis




















Comments