JEE Main Alternating Current Previous Year Questions with Solutions

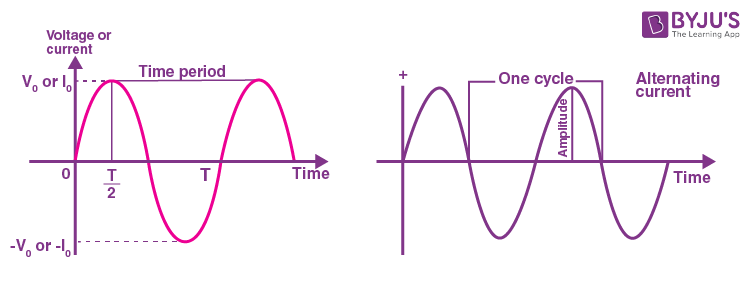
Alternating current (A.C.) changes its magnitude and polarity at a regular interval of time. The time interval between a definite value of two successive cycles is the time period and the number of cycles or number of periods per second is frequency. The maximum displacement of the wave in both the directions is called the amplitude.

Alternating current can also be produced by different methods. One common method is by using a basic single coil AC generator, which consists of two-pole magnets and a single loop of wire having a rectangular shape. In a generator, mechanical energy gets converted into electrical energy.

Download Alternating Current Previous Year Solved Questions PDF

AC is the form of current that is mostly used in home appliances. Some of the examples of alternating current include audio signal, radio signal, etc.

JEE Main Previous Year Solved Questions on Alternating Current

Q1: A series AC circuit containing an inductor (20 mH), a capacitor (120 μF) and a resistor (60 Ω ) is driven by an AC source of 24 V/50 Hz. The energy dissipated in the circuit in 60 s is

(a) 3.39 × 10³ J

(b) 5.65 × 10² J

(c) 2.26 × 10³ J

(d) 5.17 × 10² J

Solution

Impedance,

Z = (R² + (X_C – X_L)²)^1/2

X_L = ωL = (2πvL)

X_L = 6.28 × 50 × 20 × 10^–3 = 6.28 Ω

X_C = (1/ωC) = 1/(2πvC) = 1/(6.28 x 120 x 10^-6 x 50) = 26.54 Ω

X_C – X_L = 26.54  – 6.28 = 20.26

Z = ((60)² + (20.26)²)^½

Z² = 4010 Ω²

Average power dissipated, Pav = ε _rms I_rmscos Φ

P_av = ε _rms × (ε _rms/Z) x (R/Z)

P_av = (ε _rms ²/Z²) x R = [(24)²/4010] x 60 W = 8.62 W

Energy dissipated in 60 S = 8.62 x 60 = 5.17 x 10² J

Answer: (d) 5.17 x 10² J

Q2: In an AC generator, a coil with N turns, all of the same area A and total resistance R, rotates with frequency ω in a magnetic field B. The maximum value of emf generated in the coil is

(a) NAB

(b) NABR

(c) NABω

(d) NABRc

Answer: (c) In an a.c. generator, maximum emf = NABω

Q3: The phase difference between the alternating current and emf is π/2. Which of the following cannot be the constituent of the circuit?

(a) LC

(b) L alone

(c) C alone

(d) R, L

Solution

R and L cause phase difference to lie between 0 and π/2 but never 0 and π/2 at extremities

Answer: (d) R, L

Q4: Alternating current cannot be measured by D.C ammeter because

(a) A.C cannot pass through D.C ammeter

(b) A.C changes direction

(c) The average value of current for the complete cycle is zero

(d) D.C. ammeter will get damaged

Solution

The average value of A.C for the complete cycle is zero. Hence A.C cannot be measured by D.C ammeter

Answer: (c) The average value of current for the complete cycle is zero

Q5: A power transmission line feeds input power at 2300 V to a step-down transformer with its primary windings having 4000 turns. The output power is delivered at 230 V by the transformer. If the current in the primary of the transformer is 5 A and its efficiency is 90%, the output current would be

(a) 25 A

(b) 50 A

(c) 45 A

(d) 35 A

Solution

Given є_p = 2300 V, N_p = 4000

є_s = 230 V,

I_p = 5 A,

η = 90% = 0.9

η = P_o/P_i = (є_sI_s)/(є_pI_p)

I_s = ηє_pI_p/є_s = (0.9 x 2300 x 5)/230 = 45 A

Answer: (c) 45 A

Q6: A circuit connected to an ac source of emf e = e₀ sin(100 t) with t in seconds, gives a phase difference of π/4 between the emf e and current I. Which of the following circuits will exhibit this?

(a) RC circuit with R = 1 kΩ and C = 10μF

(b) RL circuit with R = 1 kΩ and L = 10mH

(c) RC circuit with R = 1 kΩ and C = 1μF

(d) RL circuit with R = 1 kΩ and L = 1mH

Solution

X_c = R

1/ωC = R

ω = 100 rad/s

Therefore, 1/100 = RC

Substituting values from option (a)

R = 1 kΩ  = 10³ Ω

C = 10μF = 10 x 10^-6 F

RC = 10³ x 10 x 10^-6  = 1/100

Therefore, option (a) is correct

Answer (a) RC circuit with R = 1 kΩ and C = 10μF

Q7: In an a.c. circuit, the instantaneous e.m.f. and current is given by

e = 100sin30t, i = 20sin(30t – π/4)

In one cycle of A.C, the average power consumed by the circuit and the wattless current are, respectively

(a) 50, 10

(b) 1000/√2 ,10

(c) 50/√2, 0

(d) 50, 0

Solution

P_avg = V_rmsI_rmscosθ

P_avg = (V₀/√2) (I₀/√2)cosθ

= (100/√2) (20/√2)cos45⁰

P_avg = 1000/√2 watt

Wattless current = I_rmssinθ

Wattless current = (I₀/√2)sinθ

= (20/√2)sin45⁰

= 10 amp

Answer: (b) 1000/√2 ,10

Q8: A coil having n turns and resistance R Ω is connected with a galvanometer of resistance 4R Ω. This combination is moved in time t seconds from a magnetic field W₁ weber to W₂ weber. The induced current in the circuit is

(a) -(W₂ – W₁)/5Rnt

(b) -n(W₂ – W₁)/5Rt

(c) -(W₂ – W₁)/Rnt

(d) -(W₂ – W₁)/5Rnt

Solution

The emf induced in the coil is e = -n(dΦ/dt)

Induced current, I = e/R’ = – (n/R’)(dΦ/dt) ——(1)

Given, R’ = R + 4R = 5R

dΦ = W₂ – W₁

dt = t

(here, W₁ and W₂ are flux associated with one turn)

Substituting the given values in equa(1) we get

I = (-n/5R)(W₂ – W₁/t)

Answer: (b) -n(W₂ – W₁)/5Rt

Q9: An alternating voltage V(t) = 220 sin100πt volts is applied to a purely resistive load of 50 Ω. The time taken for the current to rise from half of the peak value is

(a) 5 ms

(b) 2.2 ms

(c) 7.2 ms

(d) 3.3 ms

Solution

As v(t) = 220 sin100πt

So I(t) = (220/50) sin100πt

I.e., I = I_m = sin100πt

For I = I_m

t₁ = (π/2) x (1/100π) = (1/200) sec,

And for I = I_m/2

⇒ (I_m/2) = I_msin(100πt₂)

⇒ (π/6) = 100πt₂

⇒ t₂= (1/600) s

∴ t_req = (1/200) – (1/600) = (2/600) = (1/300)s =3.3 ms

Answer: (d) 3.3 ms

Q10: An arc lamp requires a direct current of 10A at 80V to function. If it is connected to a 220V (RMS), 50 Hz AC supply, the series inductor needed for it to work is close to

(a) 0.065 H

(b) 80 H

(c) 0.08 H

(d) 0.044 H

Solution

I = 10A

V = 80 V

R = 8 Ω

10 = 220/(8² + X_L²)^½

64 + X_L²= 484

X_L = √420

2π x 50L = √420

L = √420/100π

L = 0.065 H

Answer: (a) 0.065 H

Q11: In a series, LCR circuit R = 200Ω and the voltage and the frequency of the main supply is 220 V and 50 Hz respectively. On taking out the capacitance from the circuit the current lags behind the voltage by 30⁰.  The power dissipated in the LCR circuit is

(a) 242 W

(b) 305 W

(c) 210 W

(d) Zero

Solution

Tan Φ = (X_L – X_c)/R

Tan 30⁰ = X_c/R = X_c = R/√3

Tan 30⁰ = X_L/R = X_L = R/√3

X_L = X_c ⇒ Condition for resonance

So Φ = 0⁰

P = VIcos0⁰

P = V²/R = (220)²/200 = 242 W

Answer: (a) 242 W

Also Read:

Alternating Current JEE Advanced Previous Year Questions With Solutions

Alternating Current – JEE Advanced Solved Questions