Electromagnetic waves or EM waves have a vibrating electric field and magnetic field. These are the waves that propagate at the speed of light in empty space. The speed of light is equal to 3 x 108 m/s. Some of the electromagnetic waves like visible light are harmless.
X-ray is an example of an EM wave that can be harmful if the person is exposed to it for a longer time.
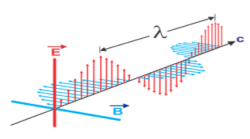
Electromagnetic waves are represented as a sinusoidal graph. The electric and magnetic fields are perpendicular to each other and are also perpendicular to the direction of propagation of waves. Electromagnetic waves are transverse in nature. The highest point of the wave is known as crest while the lowest point is known as the trough.
Download Electromagnetic Waves Previous Year Solved Questions PDF
JEE Main Previous Year Solved Questions on Electromagnetic Waves
Q1: The mean intensity of radiation on the surface of the Sun is about 108 W/m2. The RMS value of the corresponding magnetic field is closest to
(a) 10–2 T
(b) 1 T
(c) 10–4 T
(d) 102 T
Solution
Mean intensity I= (B2rms/μ0)c
B2rms = (108 x 4π x 10-7)/(3 x 108)
Brms ≈ 10-4 T
Answer: (c) 10–4 T
Q2: A plane electromagnetic wave travels in free space along the x-direction. The electric field component of the wave at a particular point of space and time is E = 6 V m–1 along the y-direction. Its corresponding magnetic field component, B would be
(a) 6 × 10–8 T along the x-direction
(b) 2 × 10–8 T along the y-direction
(c) 2 × 10–8 T along the z-direction
(d) 6 × 10–8 T along the z-direction
Solution
The direction of electromagnetic wave travelling is given by
As the wave is travelling along x-direction and E is along the y-direction.
So B must point towards the z-direction.
The magnetic field, B = E/c = 6/(3 x 108) = 2 x 10-8 T
Answer: (c) 2 × 10–8 T along the z-direction
Q3: 50 W/m2 energy density of sunlight is normally incident on the surface of a solar panel. Some part of incident energy (25%) is reflected from the surface and the rest is absorbed. The force exerted on 1m2 surface area will be close to (c = 3 × 108 m/s)
(a) 20 × 10–8 N
(b) 10 × 10–8 N
(c) 35 × 10–8 N
(d) 15 × 10–8 N
Solution
Given energy density = 50 W/m2
Here, change in momentum Δp = pf – pi
Δp = (-pi /4) – pi
Δp = -5pi /4 ∵ pi = E/c = 50 W/s/(3 x 108)
Δp/Δt = F = 丨-5pi/4丨= (5/4) x (50/(3 x 108) = 20.8 x 10-8 N ≈ 20x 10-8 N
Answer: (a) 20 × 10–8 N
Q4: A red LED emits light at 0.1 watts uniformly around it. The amplitude of the electric field of the light at a distance of 1 m from the diode is
(a) 5.48 V/m
(b) 7.75 V/m
(c) 1.73 V/m
(d) 2.45 V/m
Solution
The intensity of light, I = uav c
Also, I = P/4πr2 and uav = ½ε0E02
∴ P/4πr2 = (½)ε0E02c
Or
Here, P = 0.1 W, r = 1 m, c = 3 × 108 m s–1
1/4πε0 = 9 x 109 N C–2 m2
= 2.45 V m-1
Answer: (d) 2.45 V/m
Q5: Match List-I (Electromagnetic wave type) with List-II (Its association/application) and select the correct option from the choices given below the lists
| List-I | List-II |
| (P) Infrared waves | (i) To treat muscular strain |
| (Q) Radio waves | (ii) For broadcasting |
| (R) X-rays | (iii) To detect fracture of bones |
| (S) Ultraviolet rays | (iv) Absorbed by the ozone layer of the atmosphere |
P Q R S
(a) (i) (ii) (iii) (iv)
(b) (iv) (iii) (ii) (i)
(c) (i) (ii) (iv) (iii)
(d) (iii) (ii) (i) (iv)
Solution
Infrared waves are used to treat muscular strain. Radio waves are used for broadcasting. X-rays are used to detect the fracture of bones. Ultraviolet rays are absorbed by the ozone layer of the atmosphere.
Answer: (a)
P Q R S
(i) (ii) (iii) (iv)
Q6: During the propagation of electromagnetic waves in a medium
(a) both electric and magnetic energy densities are zero
(b) electric energy density is double of the magnetic energy density
(c) electric energy density is half of the magnetic energy density
(d) electric energy density is equal to the magnetic energy density
Solution: In an em wave, energy is equally divided between the electric and the magnetic fields.
Answer: (d) The electric energy density is equal to the magnetic energy density
Q7: The magnetic field in a travelling electromagnetic wave has a peak value of 20 nT. The peak value of electric field strength is
(a)12 V/m
(b) 3 V/m
(c) 6 V/m
(d) 9 V/m
Solution
In an electromagnetic wave, the peak value of the electric field (E0) and peak value of magnetic field (B0) are related by
E0 = B0C
E0 = (20 × 10–9 T) (3 × 108 m s–1) = 6 V/m
Answer: (c) 6 V/m
Q8: An electromagnetic wave of frequency = 3.0 MHz passes from vacuum into a dielectric medium with permittivity = 4.0. Then
(a) wavelength is doubled and the frequency remains unchanged
(b) wavelength is doubled and frequency becomes half
(c) wavelength is halved and frequency remains unchanged
(d) wavelength and frequency both remain unchanged
Solution
Step 1: Given that:
The frequency of electromagnetic wave= 3.0MHz =3×106Hz
Relative permittivity of the medium(εr)= 4
Step 2: Determination of frequency of the EM wave when passes from vacuum to dielectric medium:
- The frequency of the electromagnetic wave does not change with the change in medium.
- The wavelength and speed of the wave change with the change in the medium.
Thus, the frequency of the EM wave when it passes from vacuum to dielectric medium will not change.
Step 3: Determination of wavelength of EM wave:
The velocity of the EM wave in vacuum is given by,
c = 1/√μ0ε0
If n is the frequency of the wave and λ is the wavelength of the wave, then
c=nλ
Thus, c = 1/√μ0ε0 = nλ
n = c/λ ——-(1)
Where λ is the wavelength of EM wave in a vacuum.
Now, the Velocity of the electromagnetic wave in the medium is given by;
vmedium=1√μ0ε0μrεr
Since, c=1√μ0ε0
Therefore,
vmedium=c/√μrϵr
Where, εr and μr are the relative permittivity and relative permeability of the medium.
For dielectric medium, μr=1,
Thus,
vmedium=c/√εr
Now,
vmedium=c/√4
vmedium=c/2
Since, frequency does not change, thus,
vmedium=n×λmedium
c/2=n×λmedium
⇒ν=c/(2λmedium) …………(2)
From (1) and (2) we get;
c/λ=c/2λmedium
λmedium=λ/2
Answer: (c) wavelength is halved and frequency remains unchanged
Q9: Electromagnetic waves are transverse in nature is evident by
(a) polarization
(b) interference
(c) reflection
(d) diffraction
Answer: (a) Polarization proves the transverse nature of electromagnetic waves.
Q10: The energy associated with electric field is (UE) and with magnetic field is (UB) for an electromagnetic wave in free space. Then
(a) UE > UB
(b) UE = UB/2
(c) UE = UB
(d) UE < UB
Answer: (c) UE = UB
Q11: A 27 mW laser beam has a cross-sectional area of 10 mm2. The magnitude of the maximum electric field in this electromagnetic wave is given by [Given permittivity of space ε0 = 9 × 10–12 SI units, speed of light c = 3 × 108 m/s]
(a) 2 kV/m
(b) 0.7 kV/m
(c) 1 kV/m
(d) 1.4 kV/m
Solution
The intensity of the electromagnetic wave is given by
I = Power(P)/Area(A) = ½ ε0 E2C
E = 1.4 kV/m
Answer: (d) 1.4 kV/m
Q12: The RMS value of the electric field of the light coming from the sun is 720 N/C. The average total energy density of the electromagnetic wave is
(a) 3.3 × 10–3 J/m3
(b) 4.58 × 10–6 J/m3
(c) 6.37 × 10–9 J/m3
(d) 81.35 ×10–12 J/m3
Solution
U = (½)є0 (E2rms)+ (½μ0) (B2rms)
U = (½)є0 (E2rms) + (½μ0) (E2rms/c2)
U = (½)є0 (E2rms) + (½μ0) (E2rmsє0μ0)
U = (½)є0 (E2rms) + (½)є0 (E2rms) = є0 (E2rms)
U = (8.85 x 10-12) x (720)2 = 4.58 x10-6 Jm-1
Answer (b) 4.58 × 10–6 J/m3
Q13: Which of the following are not electromagnetic waves?
(a) cosmic rays
(b) gamma rays
(c) β-rays
(d) X-rays
Answer: (c) β-rays are not electromagnetic waves
Q14: If a source of power 4kW produces 1020 photons/second, the radiation belongs to a part of the spectrum called
(a) microwaves
(b) y-rays
(c) X-rays
(d) ultraviolet rays
Solution
Energy of a photon
E = hν = hc/λ
If n is the number of photon emitted per second
Power, P = nhc/λ
4 x 103 = (1020 x 6.62 x 10-34 x 3 x 108)/λ
λ = (1020 x 6.62 x 10-34 x 3 x 108)/(4 x 103)
λ = (19.8 x 10-6)/ (4 x 103)
λ = 4.96 x 10-9
= 49.6 Å
≈ 50 Å (x -ray)
Answer: (c) X-rays
Q15: An EM wave from the air enters a medium. The electric fields are
in air and
in medium, where the wavenumber k and frequency f refer to their values in air. The medium is non-magnetic. If εr1 and εr2 refer to relative permittivities of air and medium respectively, which of the following options is correct?
(a) εr1 /εr2 = 4
(b) εr1 /εr2 = 2
(c) εr1 /εr2 = 1/4
(d) εr1 /εr2 = ½
Solution
In the air, the EM wave is
=
In the medium, the EM wave is
During refraction, frequency remains unchanged, whereas the wavelength gets changed
k’ = 2k (From equations)
2π/λ’ = 2(2π/λ0) = λ’= λ0/2
Since, v = c/2
εr1/εr2= 1/4
Answer: (c) εr1 /εr2 = 1/4
Also Read:
X Rays JEE Advanced Previous Year Questions With Solutions
Electromagnetic Induction and Magnetism


Comments