Number of Functions

The number of functions is an important topic in sets. A relation in which each input has a particular output is called a function. If f is a function from set A to set B, then each element of A will be mapped with only one element in B. In this article, we will learn the formula to find the number of functions from the given sets and some solved examples.

Consider a set X having 6 elements and another set Y having 5 elements. Every element of set X will be mapped to one element in set Y. So, each element of X has 5 elements to be chosen from. Hence, the total number of functions will be 5×5×5.. 6 times = 5⁶.

Formula for Number of Functions

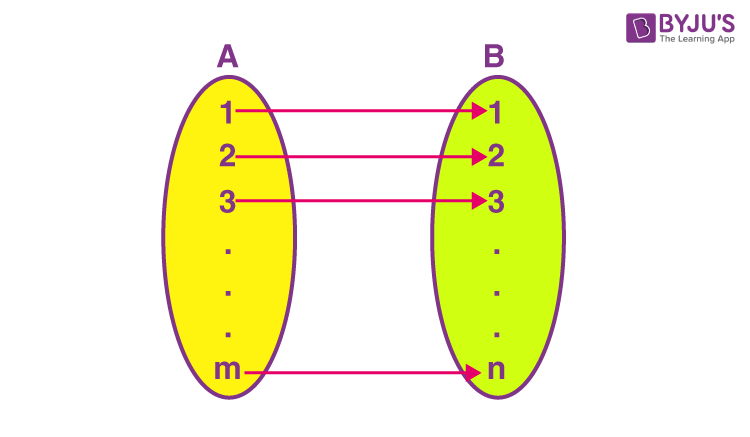
1. Number of possible functions

If a set A has m elements and set B has n elements, then the number of functions possible from A to B is n^m.

For example, if set A = {3, 4, 5}, B = {a, b}.

The total number of possible functions from A to B = 2³ = 8

2. Number of Surjective Functions (Onto Functions)

If a set A has m elements and set B has n elements, then the number of onto functions from A to B = n^m – ⁿC₁(n-1)^m + ⁿC₂(n-2)^m – ⁿC₃(n-3)^m+….- ⁿC_n-1 (1)^m.

Note that this formula is used only if m is greater than or equal to n.

For example, in the case of onto function from A to B, all the elements of B should be used. If A has m elements and B has 2 elements, then the number of onto functions is 2^m-2. From a set A of m elements to a set B of 2 elements, the total number of functions is 2^m. In these functions, 2 functions are not onto (If all elements are mapped to the 1st element of B or all elements are mapped to the 2nd element of B). So, the number of onto functions is 2^m-2.

3. Number of Injective Functions (One to One)

If set A has n elements and set B has m elements, m≥n, then the number of injective functions or one to one function is given by m!/(m-n)!.

4. Number of Bijective functions

If there is a bijection between two sets, A and B, then both sets will have the same number of elements. If n(A) = n(B) = m, then the number of bijective functions = m!.

Solved Examples – Number of Functions

Example 1:

The number of onto functions from set P = {a, b, c, d} to set Q = {u, v, w} is:

(A) 68

(B) 36

(C) 81

(D) 64

Solution:

P = {a, b, c, d}

Q = {u, v, w}

Here, n(P) = m = 4

n(Q) = n = 3

The number of onto functions = 3⁴ – ³C₁(3-1)⁴ + ³C₂(3-2)⁴

= 81 – 48 + 3

= 36.

Hence, option B is the answer.

Example 2:

The number of bijective functions from set A to itself, when A contains 106 elements, is

(A) 106

(B) 106!

(C) 106²

(D) 2¹⁰⁶

Solution:

n(A) = m = 106

The number of bijective functions = m!

= 106!

Hence, option B is the answer.

Related Video