In this article, we will explain the position of a point with respect to a hyperbola. We will discuss the three cases in which point P can lie inside, outside or on the hyperbola. Consider a point P(x₁, y₁) in the plane of the hyperbola (x²/a²) – (y²/b²) = 1. The point can be on the hyperbola, outside the hyperbola or inside the hyperbola.

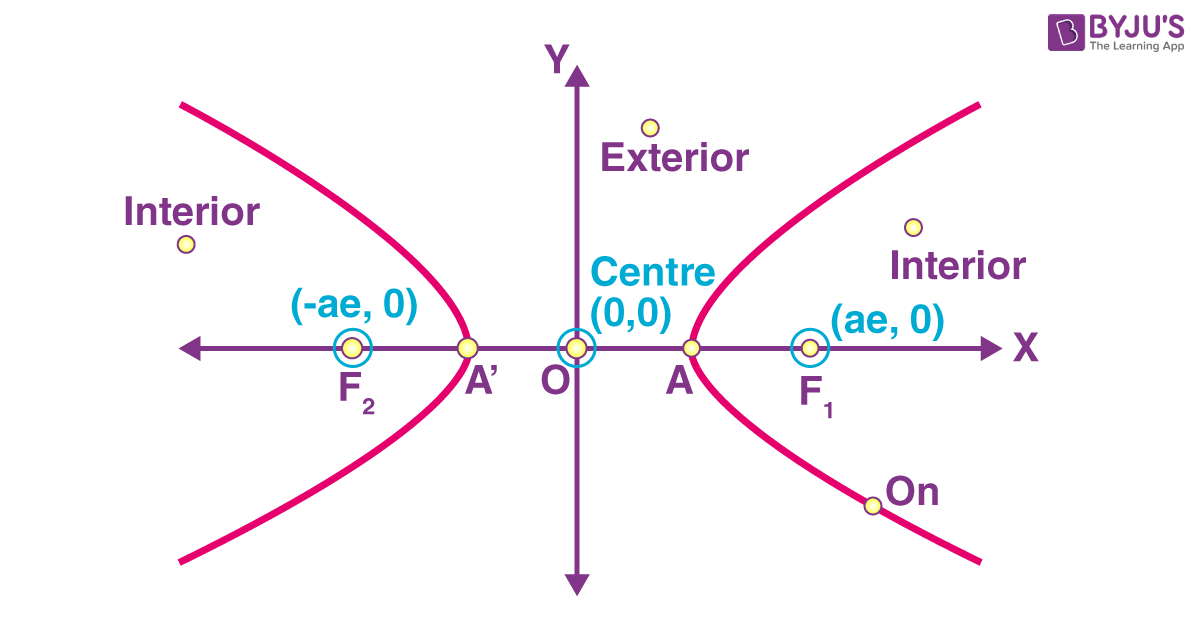
The figure given below gives you a clear idea about the interior (inside) and exterior of the hyperbola.

Steps to Check the Position of a Point with Respect to Hyperbola

Step 1: Write the equation of the hyperbola in the form

S = (x²/a²) – (y²/b²) – 1

Step 2: Substitute the point (x₁, y₁) in S.

=> S₁ = (x₁²/a²) – (y₁²/b²) – 1

Step 3:

Case 1: If S₁ > 0, then the point P(x₁, y₁) lies inside the hyperbola.

Consider an interior point F₁ (ae, 0) in the figure above.

Find S_F1 by substituting (ae, 0) in S: (x²/a²) – (y²/b²) – 1

S_F1 => (a²e²/a²) – (0/b²) – 1

=> e² – 1

> 0 (since e is the eccentricity of hyperbola >1)

=> The value of S₁ at any interior point of the hyperbola is positive.

Case 2: If S₁ = 0, then the point P(x₁,y₁) is on the hyperbola.

The value of S₁ at a point on the hyperbola is equal to zero.

Case 3: If S₁ < 0, then the point P(x₁, y₁) lies outside the hyperbola.

Consider the point O(0, 0) in the figure above.

Find S_O by substituting (0, 0) in S: (x²/a²) – (y²/b²) – 1

S_O => (0²/a²) – (0/b²) – 1

=> -1 < 0

=> The value of S at any exterior point of the hyperbola is negative.

Also, Read:

Important Properties of Hyperbola

Conic Sections

Solved Examples

Example 1:

Find the position of the point (2, -3) with respect to the hyperbola x²/9 – y²/25 = 1.

Solution:

Given equation of hyperbola x²/9 – y²/25 = 1…(i)

The point (x₁, y₁) lies outside the hyperbola x²/a² – y²/b² = 1, if x₁²/a² – y₁²/b² – 1 < 0.

If x₁²/a² – y₁²/b² – 1 = 0, then the point lies on the hyperbola x²/a² – y²/b² = 1.

If x₁²/a² – y₁²/b² – 1 > 0, then the point lies inside the hyperbola x²/a² – y²/b² = 1.

Substitute the given point (2, -3) in (i)

=> 2²/9 – (-3)²/25 – 1

= 4/9 – 9/25 – 1

= -206/225 < 0.

So, the point lies outside the hyperbola.

Example 2:

Find the position of the point (7, -3) with respect to the hyperbola 9x² – 4y² = 36.

Solution:

Given equation of hyperbola 9x² – 4y² = 36

=> S = 9x² – 4y² – 36

Substitute (7, -3) in the above equation

=> 9(49) – 4(9) – 36

= 441 – 36 – 36

= 369 > 0

So, the point (7, -3) lies inside the hyperbola.

Position of a Point with Respect to Hyperbola – Concept Video