Kerala SSLC Board Question Papers for Class 10th Maths 2019 With Solutions In PDF

Kerala SSLC or Class 10 Maths Question Paper 2019 with Answers – Free Download

Kerala SSLC (Class 10) maths 2019 question paper with solutions are provided here in a downloadable pdf format and also in the text so that the students can easily access them. Along with the solutions, they can also get the maths question paper 2019 class 10 sslc for reference. Students are able to access all the Kerala board previous year maths question papers here. SSLC question paper 2019 kerala for English medium with answers can be downloaded easily and students can practice and verify the answers provided by BYJU’S. Solving 2019 Maths question papers for class 10 will help the students to predict what type of questions will appear in the exam.

Download Kerala SSLC 2019 Maths Question Paper

Download Kerala SSLC 2019 Maths Question Paper With Solutions

Download Kerala SSLC 2019 Maths Question Paper With Solutions

KBPE Class 10th Maths Question Paper With Solution 2019

QUESTION PAPER CODE S 1935

Answer any three questions from 1 to 4. Each question carries 2 scores. [3 * 2 = 6]

Question 1: In the figure, O is the centre of the circle. ∠AOC = 80^o

[i] What is the measure of ∠ABC?

[ii] What is the measure of ∠ADC?

Solution:

Given ∠AOC = 80⁰

40^o. + ∠ADC = 180^o

∠ADC = 180^o – 40^o

∠ADC = 140^o

Question 2: [i] Write the first integer term of the arithmetic sequence (1 / 7), (2 / 7), (3 / 7) …….

[ii] What is the sum of the first 7 terms of the above sequence?

Solution:

Common difference d = 2 / 7 – 1 / 7 = 1 / 7.

Hence the first integer term = 7 / 7 = 1

d = 2 / 7 – 1 / 7

= 1 / 7

n = 7

S_n = (n / 2) (2a + [n – 1]d)

S₇ = (7 / 2) (2 * [1 / 7] + [7 – 1] * [1 / 7])

= (7 / 2) ([2 / 7] + 6 * (1 / 7))

= (7 / 2) ([2 / 7] + [6 / 7])

= (7 / 2) (8 / 7)

= 4

Question 3: [i] If C (-1, k) is a point on the line passing through the points A (2, 4) and B (4, 8) which number is k?

[ii] What is the relation between the x coordinate and the y coordinate of any point on this line?

Solution:

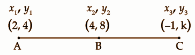
Points A, B and C are collinear.

Area of triangle ABC = 0

(1 / 2) (x₁ [y₂ – y₃] + x₂ [y₃ – y₁] + x₃ [y₁ – y₂])

|2 (8 – k) + 4 (k – 4) + (-1) (4 – 8)| = 0

16 – 2k + 4k – 16 – 4 + 8 = 0

2k = -4

k = -2

Area of triangle ABP = 0

(1 / 2) (x₁ [y₂ – y₃] + x₂ [y₃ – y₁] + x₃ [y₁ – y₂])

|2 (8 – y) + 4 (y – 4) + (x) (4 – 8)| = 0

16 – 2y + 4y – 16 – 4x = 0

2y – 4x = 0

2y = 4x

y = 2x

2x – y = 0

Question 4: [i] Find P(1) if P(x) = x² + 2x + 5

[ii] If (x – 1) is a factor of x² + 2x + k, what is the value of k?

Solution:

P(1) = 1² + 2 * 1 + 5

= 1 + 2 + 5

P(1) = 8

x – 1 = 0

x = 1

(1)² + 2(1) + k = 0

1 + 2 + k = 0

k = -3

Answer any five questions from 5 to 11. Each question carries 3 scores. [5 * 3 = 15]

Question 5: [i] What is the remainder on dividing the terms of the arithmetic sequence 100, 107, 114 ….. by 7?

[ii] Write the sequence of all three-digit numbers. Which leaves the remainder 3 on division by 7? Which is the last term of this sequence?

Solution:

d = 7

Remainder = 100 / 7 = 2

Hence the last three-digit term = 997.

Question 6: AB is the diameter of the circle. D is the point on the circle.

∠ACB + ∠ADB + ∠AEB = 270^o. The measure of one among ∠ACB, ∠ADB and ∠AEB is 110^o. Write the measures of ∠ACB, ∠ADB, ∠AEB.

Solution:

∠ADB = 90⁰ ( Measurement of semi circle angle)

∠ACB + ∠ADB + ∠AEB = 270⁰ (given)

∠ACB + 90^o + ∠AEB = 270⁰

∠ACB + ∠AEB = 270⁰ – 90^o = 180⁰

The given condition is that any one of the angles ∠ACB, ∠AEB be 110⁰.

Take ∠ACB = 110⁰

Hence ∠AEB = 180^o – 110^o = 70⁰

So the angles , ∠ADB = 90⁰ , ∠ACB = 110⁰ , ∠AEB = 70⁰.

Question 7: If x is a natural number,

[a] What number is to be added to x² + 6x to get a perfect square?

[b] If x² + ax + 16 is a perfect square number, then which number is a?

[c] If x² + ax + b is a perfect square, prove that a² = 4b.

Solution:

Given x² + 6x

a = x

b = ?

b = 6x / 2x = 3

Perfect square = b² = 3² = 9.

Hence 9 is to be added to them.

[b] Given, x² + ax + 16 is perfect square

This is the form of a² + 2ab + b² = (a + b)²

2ab = ax

a = x

b² = 16

b = √16 = 4

So, (x + 4)² = x² + ax + 16

Hence a = 2ab = 2 × 4 = 8.

b = (a / 2)²

b = a² / 4

a² = 4b

Question 8: In the figure, ∠B = 90^o, ∠C = 44^o.

[a] What is the measure of A?

[b] Which among the following is tan 44^o:

(AB / BC) , (AB / AC), (BC / AB), (BC / AC)

[c] Prove that tan 44^o * tan 46^o = 1

Solution:

∠A + 90^o + 44^o = 180^o

∠A = 180^o – 90^o – 44^o

∠A = 46^o

tan 44^o = opposite / adjacent

= AB / BC {from the figure}

= tan 44^o * cot (90^o – 46^o) [tan θ = cot (90 – θ)]

= tan 44^o * cot 44^o

= tan 44^o * [1 / tan 44^o]

= 1

= RHS

Question 9: Draw a circle of radius 3 centimetres. Mark a point P at a distance of 6cm from the centre of the circle. Draw tangents from P to the circle.

Solution:

Steps of construction:

• Draw a circle of radius 3cm with O as the centre.
• From the centre O, draw OP = 6cm and perpendicular to OP marking it as M.
• Draw another circle with centre M cutting T and R respectively.
• Join PT and PR which are the required tangents.

Question 10: [i] Find the coordinates of the point on the x-axis, which is at a distance of 4 units from (3, 4).

[ii] Find the coordinates of the point on the x-axis at a distance of 5 units from (3, 4).

Solution:

4 = √(x – 3)² + (0 – 4)²

On squaring both sides,

4² = (x – 3)² + 16

x – 3 = 0

x = 3

A (3, 0) is the required point.

AB = 5

√(x – 3)² + (0 – 4)² = 5

On squaring both sides,

(x – 3)² + 16 = 5²

(x – 3)² + 16 = 25

(x – 3)² = 25 – 16

(x – 3)² = 9

(x – 3) = ± 3

x – 3 = 6

x = 6

x – 3 = -3

x = 0

Hence, (6, 0) and (0, 0) is the required point.

Question 11: The given figure is the lateral face of a square pyramid. AB = AC = 25 centimeters and BD = DC = 15 centimeters.

[i] What is the length of its base edge?

[ii] Find the lateral surface area of the pyramid.

Solution:

Side of the base = diagonal / √2

= (30 / √2) * (√2 / √2)

= 15 √2 cm

= 15 * 1.414

= 17.210

Side of the base = 17.210 cm

Lateral surface area = (1 / 2) * perimeter of the base * slant height

= (1 / 2) * (17.21) * 4 * 25

= 860.50 cm²

Answer any 7 questions from 12 to 21. Each question carries 4 scores. [7 * 4 = 28]

Question 12: In triangle ABC, ∠A = 30^o, ∠B = 80^o, the circumradius of the triangle is 4 centimetres. Draw the triangle. Measure the length of its smallest side.

Solution:

Steps of construction:

• Draw a circle of radius 4cm having a centre at O.
• Make an angle ∠BOC = 60^o.
• Construct an angle ∠CBA = 80^o.
• Join AC.
• △ABC is the required triangle.

∠A + ∠B + ∠C = 180^o

30^o + 80^o + ∠C = 180^o

∠C = 180^o – 110^o

∠C = 70^o

30^o < 70^o < 80^o

∠A < ∠C < ∠B

The smallest angle is ∠A.

BC is the smallest side of △ABC.

Question 13: Find the following sums:

[i] 1 + 2 + 3 + …… 100

[ii] 1 + 3 + 5 + …… 99

[iii] 2 + 4 + 6 + …… 100

[iv] 3 + 7 + 11 + ……. 199

Solution:

a = 1

d = 2 – 1 = 1

Last term = 100 = l

l = a + (n – 1) d

100 = 1 + (n – 1) 1

100 = 1 + n – 1

n = 100

S_n = (n / 2) (n + 1)

S₁₀₀ = (100 / 2) (100 + 1)

= (50) * (101)

= 5050

a = 1

d = 3 – 1 = 2

Last term = 99 = l

l = a + (n – 1) d

99 = 1 + (n – 1) 2

99 = 1 + 2n – 2

99 = 2n – 1

100 = 2n

100 / 2 = n

50 = n

S_n = (n / 2) (a + a_n)

S₅₀ = (50 / 2) (1 + 99)

= (25) * (100)

= 2500

a = 2

d = 4 – 2 = 2

Last term = 100 = l

l = a + (n – 1) d

100 = 2 + (n – 1) 2

100 = 2 + 2n – 2

100 = 2n

n = 100 / 2

n = 50

S_n = (n / 2) (a + a_n)

S₅₀ = (50 / 2) (2 + 100)

= (25) * (102)

= 2550

a = 3

d = 7 – 3 = 4

Last term = 199 = l

l = a + (n – 1) d

199 = 3 + (n – 1) 4

199 = 3 + 4n – 4

199 = 4n – 1

200 / 4 = n

n = 50

S_n = (n / 2) (a + a_n)

S₅₀ = (50 / 2) (3 + 199)

= (25) * (202)

= 5050

Question 14: A box contains some green and blue balls. 7 red balls are put into it. Now the probability of getting a red ball from the box is 7 / 24 and that of the blue ball is 1 / 6.

[i] How many balls are there in the box?

[ii] How many of them are blue?

[iii] What is the probability of getting a green ball from the box?

Solution:

Let the number of green balls be x.

The number of blue balls is y.

Number of red balls = 7

Total number of balls = x + y + 7

P (red ball) = 7 / 24

P (blue ball) = 1 / 3

7 / [x + y + 7] = 7 / 24

24 = x + y + 7

24 – 7 = x + y

17 = x + y —- (1)

P (blue ball) = 1 / 3

y / [x + y + 7] = 1 / 3

3y = x + y + 7

2y = x + 7

-x + 2y = 7 —- (2)

On adding equation (1) and (2),

17 = x + y

-x + 2y = 7

_______

3y = 24

y = 24 / 3

y = 8

Put y = 8 in equation (1),

17 = x + 8

17 – 8 = x

x = 9

Total number of balls = 8 + 9 + 7 = 24

y / 24 = 1 / 3

3y = 24

y = 8

Question 15: Land is acquired for road widening from a square ground, as shown in the figure. The width of the acquired land is 2 meters. Area of the remaining ground is 440 square meters.

[i] What is the shape of the remaining ground?

[ii] What is the length of the remaining ground?

Solution:

Given,

Area = 440 m²

L * B = 440

x * (x – 2) = 440

x² – 2x = 440

x² – 2x – 440 = 0

(x – 22) (x + 20) = 0

x = 22 , -20

Since the values must be positive, x = 22 is taken.

Length = 22m

Breadth = 22 – 2 = 20m

Question 16: In the figure, P is the centre of the circle. A, B and D are points on the circle. ⦣P = 90^o, AD = 5cm.

(a) What is the measure of ⦣A?

(b) What is the area of the triangle APD?

(c) Find the area of the parallelogram ABCD.

Solution:

⦣A = ⦣D [angle opposite to equal side are equal]

⦣A + ⦣ADP + ⦣APD = 180^o [angle sum property of a triangle]

⦣A + ⦣A + 90^o = 180^o

2⦣A = 90^o

⦣A = 45^o

sin 45^o = PD / AD

1 / √2 = PD / 5

5 / √2 = PD = AP

Area of △ADP = (1 / 2) * AP * PD

= (1 / 2) * (5 / √2) * (5 / √2)

= 25 / 4 cm²

= AB * PD

= 2AP * PD

= 2 * (5 / √2) * (5 / √2)

= 25 cm²

Question 17: [a] Draw the coordinates and mark the points A (1, 1), B (7, 1).

[b] Draw an isosceles triangle ABC with AB as the hypotenuse.

[c] Write the coordinates of C.

Solution:

AC = BC

√(x – 1)² + 1 = √(x – 7)² + 1

On squaring both sides,

(x – 1)² + 1 = (x – 7)² + 1

x² + 1 – 2x + 1 = x² + 49 – 14x + 1

-2x + 14x = 49 – 1

12x = 48

x = 48 / 12

x = 4

C (4, 0) is the required point.

Coordinate of C (4, 4) [AD = BC = CD]

The midpoint of the hypotenuse is equal distance from the vertex of the triangle.

Question 18: In the figure, chord BC is extended to P. Tangent from P to the circle is PA. AQ is the bisector of ⦣BAC.

[a] Write one pair of equal angles from the figure.

[b] If ⦣PAC = x and ⦣PCA = y, then prove that ⦣BAC = y – x.

[c] Prove that ⦣PAQ = [y +x] / 2

Solution:

⦣ACP = ⦣BAC + ⦣ABC [exterior angle property]

y = ⦣BAC + x

⦣BAC = y – x

= x + (1 / 2) * ⦣BAC

= x + (1 / 2) * (y – x)

= x + (1 / 2) y – (1 / 2) x

⦣PAQ = (1 / 2) (x + y)

Question 19: If (x – 1) is a factor of the second-degree polynomial P (x) = ax² + bx + c and P(0) = -5.

[a] What is the value of c?

[b] Prove that a + b = 5.

[c] Write a second-degree polynomial whose one factor is x – 1.

Solution:

x – 1 = 0

x = 1

P(1) = 0

a (1)² + b * 1 + c = 0

a + b + c = 0 —- (1)

Now, at x = 0, P(0) = -5

a * 0 + b * 0 + c = -5

c = -5

a + b – 5 = 0

a + b = 5

Question 20: A circular sheet of paper is divided into two sectors. The central angle of one of them is 160^o.

[a] What is the central angle of the remaining sector?

[b] These sectors are bent into cones of maximum volume. If the radius of the small cone is 8 centimetres, what is the radius of the other?

[c] What is the slant height of the cone?

Solution:

2𝛑R₁ = 2𝛑r (θ₁) / 360^o

8 = r * (160^o / 360^o)

r = (360^o * 8) / 160^o

r = 18cm

2𝛑R₂ = 2𝛑r (θ₂) / 360^o

R₂ = (18 * 200^o) / 360^o

R₂ = 10cm

Slant height (l₂) = 18cm

Question 21: Equation of the line AB is 3x – 2y = 6. P is a point on the line. The line intersects the y-axis at A and the x-axis at B.

[a] What is the x coordinate of A?

[b] What is the length of OA?

[c] What is the length of OB?

[d] The x coordinate and the y coordinate of P are the same. Find the coordinates of P.

Solution:

Given, the equation of line AB is 3x – 2y = 6

A, B, P are collinear.

Area of △ABP = 0

(1 / 2) [0 (0 – x) + 2 (x + 3) + x (-3 -0)] = 0

2x + 6 – 3x = 0

x = 6

Hence, the coordinates of P are (6, 6).

Answer any 5 questions from 22 to 28. Each question carries 5 scores. [5 * 5 = 25]

Question 22: If the terms of the arithmetic sequence (2 / 9), (3 / 9), (4 / 9), (5 / 9), ……. Are represented as x₁, x₂, …. then

[a] x₁ + x₂ + x₃ =

[b] x₄ + x₅ + x₆ =

[c] Find the sum of the first 9 terms.

[d] What is the sum of the first 300 terms?

Solution:

= (2 / 9) + (3 / 9) + (4 / 9)

= 9 / 9

= 1

= (5 / 9) + (6 / 9) + (7 / 9)

= (18 / 9)

= 2

a = 2 / 9

d = (3 / 9) – (2 / 9) = (1 / 9)

S_n = (n / 2) (2a + [n – 1]d)

S₉ = ( 9 /2) (2 * [2 / 9] + [9 – 1] * (1 / 9))

= (9 / 2) [(4 / 9) + (8 / 9)]

= (9 / 2) (12 / 9)

= 6

a = 2 / 9

d = (3 / 9) – (2 / 9) = (1 / 9)

S_n = (n / 2) (2a + [n – 1]d)

S₃₀₀ = ( 300 /2) (2 * [2 / 9] + [300 – 1] * (1 / 9))

= (300 / 2) [(4 / 9) + (299 / 9)]

= (150) (303 / 9)

= 5050

Question 23: Draw a rectangle of area 12 square centimetres. Draw a square having the same area.

Solution:

For the given rectangle,

Area = 12cm²

x * y = 12cm²

For a square, x = y.

x * x = 12cm²

x² = 12cm²

x = 2√3 cm

Question 24: A boy standing at one bank of a river sees the top of a tree on the other bank directly opposite to the boy at an elevation of 60^o. Stepping 40 meters back, he sees the top of the elevation at 30^o.

[a] Draw a rough sketch and find the height of the tree.

[b] What is the width of the river?

Solution:

Let AB be h and CB be x.

In △ABC,

tan 60^o = AB / BC

√3 = h / x

h = √3x —- (1)

In △ABD,

tan 30^o = AB / BD

1 / √3 = h / x + 40

x + 40 = √3 (√3x) — (2)

x + 40 = 3x

40 = 2x

x = 20

h = 20√3 m

Width of the river is 20m and the height of the tree is 20√3m.

Question 25: Circle with centre O touches the sides of a triangle at P, Q and R, AB = AC, AQ = 4cm and CQ = 6cm.

[a] What is the length of CP?

[b] Find the perimeter and the area of the triangle.

[c] What is the radius of the circle?

Solution:

CP = 6cm

For the area of △ABC,

s = [AB + BC + CA] / 2

= [10 + 12 + 10] / 2

= 16cm

Area of △ABC = √s (s – a) (s – b) (s – c)

= √(16) (16 – 10) (16 – 12) (16 – 10)

= √16 * 6 * 4 * 6

= 48cm²

48 = (1 / 2) * 10 * r + (1 / 2) * 12 * r + (1 / 2) * 10 * r

48 * 2 = r (10 + 12 + 10)

48 * 2 = 32 * r

r = 3cm

Question 26: Radius of a cylinder is equal to its height. If the radius is taken as ‘r’, the volume of the cylinder is 𝛑r² * r = 𝛑r³. Like this find the volumes of the solids, with the following measures.

[a] What is the ratio of the volumes of the cone, hemisphere, cylinder and the sphere?

[b] A solid metal sphere of radius 6cm is melted and recast into solid cones of radius 6cm and height 6cm. Find the number of cones.

Solution:

= (1 / 3) : (2 / 3) : 1 : (4 / 3)

= 1 : 2 : 3 : 4

Number of cones = Volume of the sphere / Volume of the cone

= [(4 / 3) 𝛑r³] / [𝛑R²h / 3]

= {[4 * 𝛑 * 6³] / (3)} / {[𝛑 * 6² * 6] / (3)}

= 4

Question 27: C is at the centre of the circle passing through the origin. Circle cuts the y-axis at A (0, 4) and the x-axis at B(4, 0).

[a] Write the coordinates of C.

[b] Write the equation of the circle.

[c] (0, 0) is a point on the circle. There is one more point on the circle with x and y coordinates equal. Which is that?

Solution:

x = [4 + 0] / 2

= 4 / 2

x = 2

y = [4 + 0] / 2

= 4 / 2

y = 2

The coordinates of C are (2, 2).

(x – 2)² + (y – 2)² = [√(4 – 2)² + (0 – 2)²]²

x² + 4 – 4x + y² + 4 – 4y = 8

x² + y² – 4x – 4y = 0

x² + x² – 4x – 4x = 0

2x² – 8x = 0

x = 0, 4

The required point is (4, 4).

Question 28: The table below shows the number of children in a class, sorted according to their heights.

If the students are directed to stand in a line according to the order of their heights starting from the smallest, then

[a] The height of the child at what position is taken as the median?

[b] What is the assumed height of the child in the 17th position?

[c] Find the median height.

Solution:

Median is taken as [N + 1] / 2

= [45 + 1] / 2

= 46 / 2

= 23

The height of the child at the 23^rd position is taken as the median.

= 150 + [22.5 – 16] / 10 * (10)

= 150 + 6.5

= 156.5

Question 29: Read the following. Understand mathematical concepts in it and answer the questions that follow.

The remainders obtained on dividing the powers of two by 7 have an interesting property.

We can understand it from the table given below.

If the powers are 1, 4, 7 ….. the remainder is 2.

If the powers are 3, 6, 9 ….. the remainder is 1.

[a] What is the remainder on dividing 2⁸ by 7?

[b] Write the sequence of powers of 2 leaving remainder 1 on division by 7.

[c] Check whether 2019 is a term of arithmetic sequence 3, 6, 9 …….

[d] What is the remainder on dividing 2²⁰¹⁹ by 7?

[e] Write the algebraic form of the arithmetic sequence 1, 4, 7 ……

[f] Write the algebraic form of the sequence 2¹, 2⁴, 2⁷ ….. [powers of two leaving remainder 2 on division by 7].

Solution:

2019 = 3 (n – 1) 3

2019 = 3n – 9

2019 + 9 = 3n

2018 = 3n

2018 / 3 = n

n = 673 terms

a_n = 1 + (n – 1)3

= 1 + 3n – 3

a_n = 3n – 2

So, the algebraic form is 2^3n-2.