Top Banner

Linear Correlation Coefficient Formula

To find out the relation between two variables in a population, linear correlation formula is used. To see how the variables are connected we will use the linear correlation. Also known as “Pearson’s Correlation”, a linear correlation is denoted by r” and the value will be between -1 and 1.

The elements denote a strong relationship if the product is 1. Similarly, if the coefficient comes close to -1, it has a negative relation. If the Linear coefficient is zero means there is no relation between the data given.

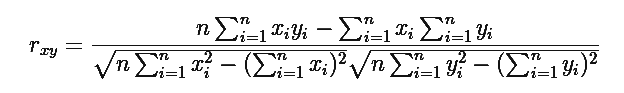
Where “n” is the number of observations, “xi” and “yi “are the variables.

Also Check: Correlation Coefficient Formulas

Solved Examples

Question 1: Calculate the linear correlation coefficient for the following data. X = 4, 8 ,12, 16 and Y = 5, 10, 15, 20.

Solution:

Given variables are,

X = 4, 8 ,12, 16 and Y = 5, 10, 15, 20

For finding the linear coefficient of these data, we need to first construct a table for the required values.

x y x2 y2 XY
4 5 16 25 20
8 10 64 100 80
12 15 144 225 180
16 20 256 400 320
Σ x = 40 Σ y =50 480 750 600

According to the formula of linear correlation we have,

\(\begin{array}{l}r(xy)=\frac{(4\times 600)-(40\times 50)}{\sqrt{4(480)-40^{2}}\sqrt{4(750)-50^{2}}}\end{array} \)

 

\(\begin{array}{l}r(xy)=\frac{2400-2000}{\sqrt{1920-1600}\sqrt{3000-2500}}\end{array} \)

 

\(\begin{array}{l}r(xy)=\frac{400}{\sqrt{320}\sqrt{500}}\end{array} \)

 

\(\begin{array}{l}r(xy)=\frac{400}{17.89\times 22.36}\end{array} \)

 

\(\begin{array}{l}r(xy)=\frac{400}{400} = 1\end{array} \)

 

Therefore, r(xy) = 1

FORMULAS Related Links
Frustum Of A Cone Formula Derivation Rotational Inertia Formula
Coefficient Of Friction Formula Perimeter Of Square Formula
Area Of Circle Formula Product Moment Correlation Formula
Midpoint Formula Area Of Rhombus
Area And Volume Of Cylinder Mass Formula

Comments

Leave a Comment

Your Mobile number and Email id will not be published.

*

*