Correlation coefficient formula is given and explained here for all of its types. There are various formulas to calculate the correlation coefficient and the ones covered here include Pearson’s Correlation Coefficient Formula, Linear Correlation Coefficient Formula, Sample Correlation Coefficient Formula, and Population Correlation Coefficient Formula. Before going to the formulas, it is important to understand what correlation and correlation coefficient is. A brief introduction is given below and to learn about them in detail, click the linked article.
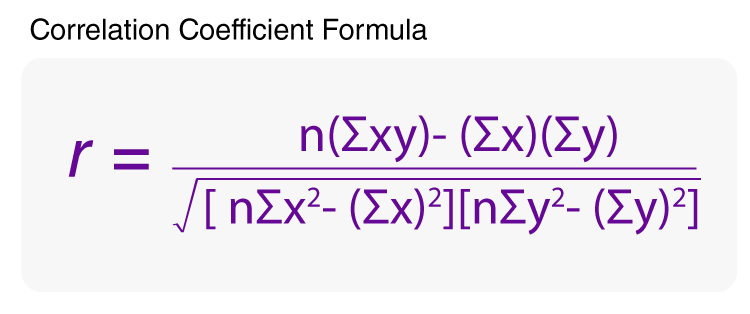
Formula to Calculate Correlation Coefficient
About Correlation Coefficient
The correlation coefficient is a measure of the association between two variables. It is used to find the relationship is between data and a measure to check how strong it is. The formulas return a value between -1 and 1, where -1 shows negative correlation and +1 shows a positive correlation.
The correlation coefficient value is positive when it shows that there is a correlation between the two values and the negative value shows the amount of diversity among the two values.
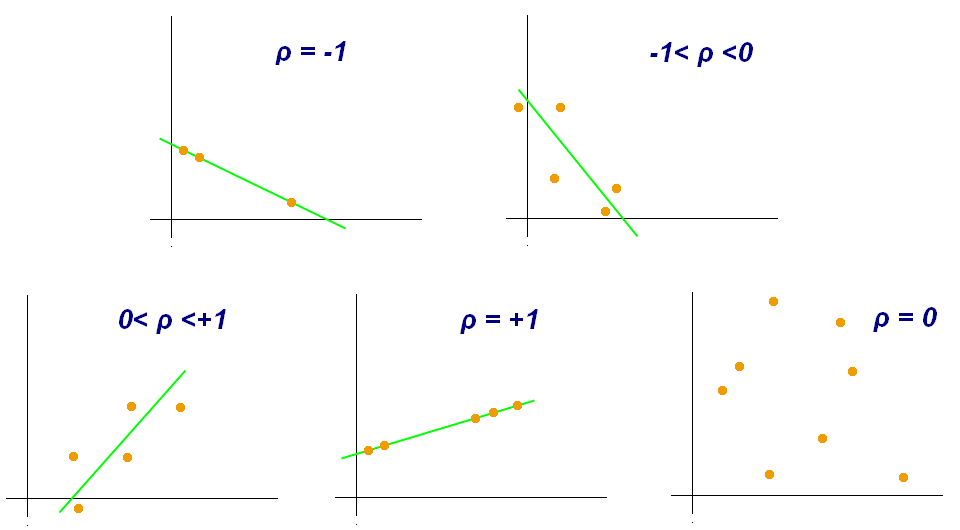
Types of Correlation Coefficient Formula
There are several types of correlation coefficient formulas. But, one of the most commonly used formulas in statistics is Pearson’s Correlation Coefficient Formula. The formulas for all the correlation coefficient are discussed below.
Pearson’s Correlation Coefficient Formula
Also known as bivariate correlation, the Pearson’s correlation coefficient formula is the most widely used correlation method among all the sciences. The correlation coefficient is denoted by “r”.
To find r, let us suppose the two variables as x & y, then the correlation coefficient r is calculated as:
Notations:
| n | Quantity of Information |
| Σx | Total of the First Variable Value |
| Σy | Total of the Second Variable Value |
| Σxy | Sum of the Product of & Second Value |
| Σx2 | Sum of the Squares of the First Value |
| Σy2 | Sum of the Squares of the Second Value |
Linear Correlation Coefficient Formula
The linear correlation coefficient formula is given by the following formula

Sample Correlation Coefficient Formula
Here, Sx and Sy are the sample standard deviations, and Sxy is the sample covariance.
Population Correlation Coefficient Formula
The population correlation coefficient uses σx and σy as the population standard deviations and σxy as the population covariance.
Relation Between Correlation Coefficient and Covariance Formulas
Here, Cov (x,y) is the covariance between x and y while σx and σy are the standard deviations of x and y.
Also Check: Covariance Formula
Practice Questions from Coefficient of Correlation Formula
- Question 1: Find the linear correlation coefficient for the following data. X = 4, 8 ,12, 16 and Y = 5, 10, 15, 20.
- Question 2: Calculate correlation coefficient for x = 100, 106, 112, 98, 87, 77, 67, 66, 49 and y = 28, 33, 26, 27, 24, 24, 21, 26, 22.
- Question 3: What will be the correlation coefficient for X and Y values for the given values: X= (1,2,3,4,5) and Y= {11,22,34,43,56}
Additional Topics Related to Correlation Coefficient Formula
Keep visiting BYJU’S and learn more such maths formulas and get various other study materials like exam papers, preparation tips, simplified lessons, etc. Also, register at BYJU’S now to access 1000+ hours of video lessons from different subjects and for different classes.

Comments