An angle is formed when two rays are joined together at a common point. The common point here is called node or vertex and the two rays are called arms of the angle. The angle is represented by the symbol ‘∠’. The word angle came from the Latin word “Angulus”. Learn more about lines and angles here.
The angle is usually measured in degrees, using a protractor. Degrees 30°, 45°, 60°, 90°, 180° shows different angles here. The types of angles are based on the values of angles in degrees.
We can also represent angles in radians, i.e., in terms of pi (π). 180 degrees is equal to π in radians.
| Table of contents: |
Definition
An angle is a form of geometrical shape, that is constructed by joining two rays to each other at their end-points. The angle can also be represented by three letters of the shape that define the angle, with the middle letter being where the angle actually is (i.e.its vertex). Angles are generally represented by Greek letters such as θ, α, β, etc.
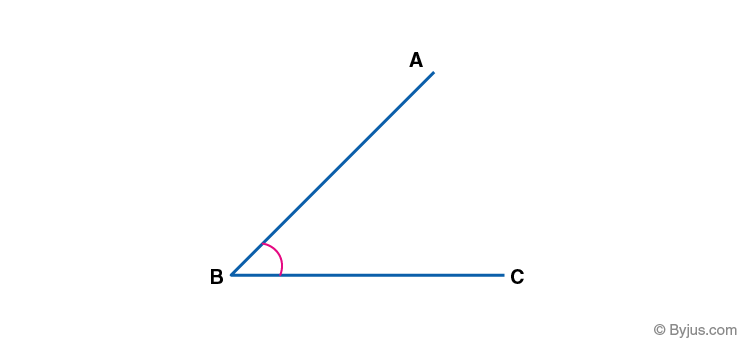
Eg. ∠ABC, where B is the given angle.
Angle measurement terms are – degree °, radians or gradians.
The amount of rotation about the point of intersection of two planes (or lines) which is required to bring one in correspondence with the other is called an Angle.
For More Information On Parts Of An Angle, Watch The Below Video:

Types of Angles
There are majorly six types of angles in Geometry. The names of all angles with their properties are:
- Acute Angle: It lies between 0° to 90.
- Obtuse Angle: It lies between 90° to 180°
- Right Angle: The angle which is exactly equal to 90°
- Straight Angle: The angle which is exactly equal to 180°
- Reflex Angle: The angle which is greater than 180 degrees and less than 360 degrees
- Full Rotation: The complete rotation of angle equal to 360 degrees
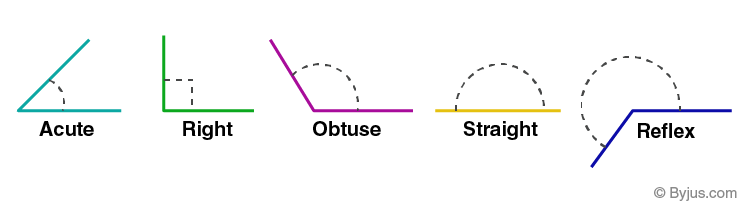
Note: Sometimes full rotation is not considered as a kind of angle. Therefore, in such cases, we consider there are five types of angles.
| Type of angles | Description |
| Acute Angle | < 90° |
| Obtuse Angle | > 90° |
| Right Angle | = 90° |
| Straight Angle | =180° |
| Reflex Angle | >180° |
| Full rotation/complete angle | =360° |
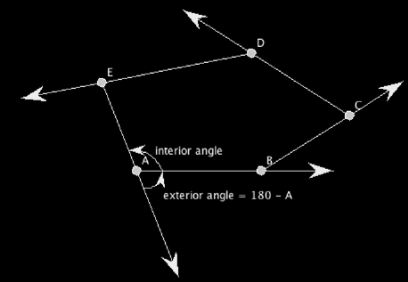
Interior and Exterior Angles
In case of a polygon, such as a triangle, quadrilateral, pentagon, hexagon, etc., we have both interior and exterior angles.
- Interior angles are those that lie inside the polygon or a closed shape having sides and angles.
- Exterior angles are formed outside the shape, between any side and line extended from adjacent sides.
For example, an image of a pentagon is given here, representing its interior angles and exterior angles.
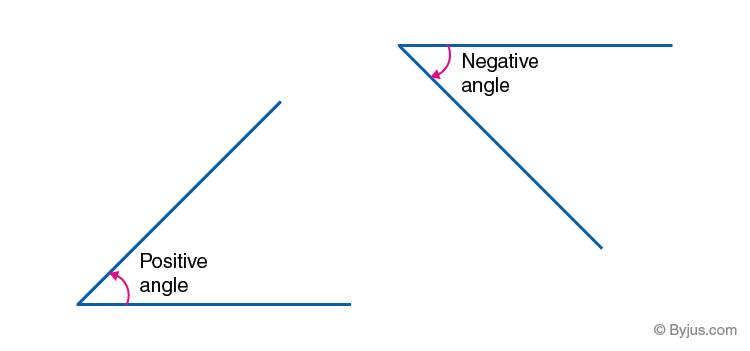
Positive & Negative Angles
- Positive Angle- An Angle measured in Anti-Clockwise direction is Positive Angle.
- Negative Angle- An angle measured in Clockwise direction is Negative Angle.
Parts of Angles
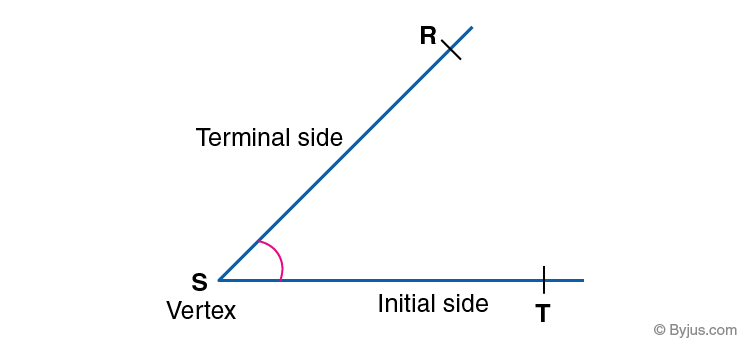
- Vertex- The corner points of an angle is known as Vertex. It is the point where two rays meet.
- Arms– The two sides of angle, joined at a common endpoint.
- Initial Side – It is also known as the reference line. All the measurements are done taking this line as the reference.
- Terminal Side- It is the side (or ray) up to which the angle measurement is done.
Angle Measurement
To measure everything in this world, we need a unit in a similar angle measurement requires three units of measurement :
Degree of an Angle
It is represented by ° (read as a degree). It most likely comes from Babylonians, who used a base 60 (Sexagesimal) number system. In their calendar, there was a total of 360 days. Hence, they adopted a full angle to be 360°. First, they tried to divide a full angle into angles using the angle of an equilateral triangle. Later, following their number system (base 60), they divided 60° by 60 and defined that as 1°. Sometimes, it is also referred to as arc degree or arc-degree which means the degree of an arc.
An angle is said to be equal to 1° if the rotation from the initial to the terminal side is equal to 1/360 of the full rotation.
A degree is further divided into minutes and seconds. 1′ (1 minute) is defined as one-sixtieth of a degree and 1” (1 second) is defined as one-sixtieth of a minute. Thus,
1°= 60′ = 3600”
Radian of an Angle
This is the SI unit of angle. Radian is mostly used in Calculus. All the formula for derivatives and integrals hold true only when angles are measured in terms of a radian. It is denoted by ‘rad’.
The length of the arc of a unit circle is numerically equal to the measurement in radian of the angle that it subtends.
In a complete circle, there are 2π radians.
360 = 2π; radian
Therefore, 1 radian = 180°/π
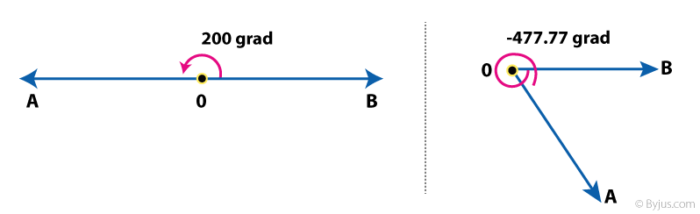
Gradian of an Angle
This unit is least used in Maths. It is also called a gon or a grade.
An angle is equal to 1 gradian if the rotation from the initial to terminal side is 1/400 of the full rotation. Hence, the full angle is equal to 400 gradians.
It is denoted by ‘grad’.
Figure 3 shows the example of angles in gradian.
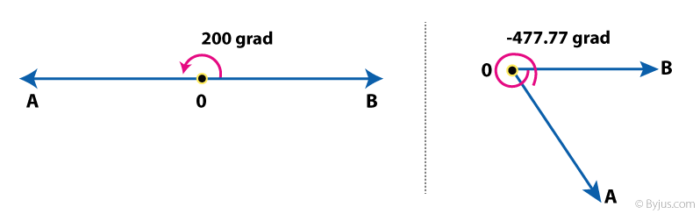
Figure 3: Angle Measurement in Gradian
Practice Problems
Draw angles using a protractor for the following measurements:
- 45 degrees
- 55 degrees
- 70 degrees
- 90 degrees
- 130 degrees
Frequently Asked Questions – FAQs
What is an angle?
What are the six types of angles?
Acute angle
Obtuse angle
Right angle
Straight angle
Reflex angle
Full rotation
How angles are measured?
What is the value of an angle equal to 60 degrees, in radians?
Since, 180 degrees equals to π, therefore,
60 degrees = π/180 x 60 = π/3 (in radians)


Comments