Coincident Lines

The lines which coincide or lie on top of each other are called coincident lines. You may have learned about different types of lines in Geometry, such as parallel lines, perpendicular lines, with respect to a two-dimensional or three-dimensional plane.

In the case of parallel lines, they are parallel to each other and have a defined distance between them. On the other hand, perpendicular lines are lines which intersect each other at 90 degrees. But, both parallel lines and perpendicular lines do not coincide with each other.

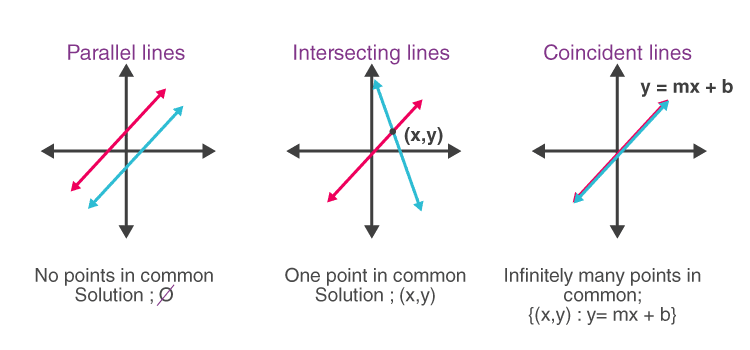
Apart from these three lines, there are many lines which are neither parallel, perpendicular, nor coinciding. They could be oblique lines or intersecting lines, which intersect at different angles, instead of perpendicular to each other.

Coincident Lines Definition

The word ‘coincide’ means that it occurs at the same time. In terms of Maths, the coincident lines are lines that lie upon each other in such a way that when we look at them, they appear to be a single line, instead of double or multiple lines.

If we see in the figure of coincident lines, it appears as a single line, but in actual we have drawn two lines here. First, we drew a line of purple color and then on top of it drew another line of black color.

Related Links:

• Concurrent Lines
• Properties Of Parallel Lines
• Lines And Angles

Coincident Lines Equation

When we consider the equation of a line, the standard form is:

y = mx + b

Where m is the slope of the line and b is the intercept.

Equation of Parallel Lines:

Now, in the case of two lines which are parallel to each other, we represent the equations of the lines as:

y = m₁x + b₁

And y = m₂x + b₂

For example, y = 2x + 2 and y = 2x + 4 are parallel lines. Here, the slope is equal to 2 for both the lines and the intercept difference between them is 2. Hence, they are parallel at a distance of 2 units.

Equation of Coincident Lines:

When we speak about coincident lines, the equation for lines is given by;

ax + by = c

When two lines are coinciding to each other, then there could be no intercept difference between them.

For example, x + y = 2 and 2x + 2y = 4 are coinciding lines. The second line is twice the first line.

Because if we put ‘y’ on the Left-hand side and the rest of the equation on the Right-hand side, then we get;

First Line: y = 2 – x …… (1)

Second line: 2y = 4 – 2x

2y = 2(2 – x)

y = 2 – x ………………….(2)

From equation (1) and (2),

Both the lines are the same.

Hence, they coincide.

Coincident lines Formula

Suppose a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0 be the pair of linear equations in two variables. The lines representing these equations are said to be coincident if;

a₁/a₂ = b₁/b₂ = c₁/c₂

Here, the given pair of equations is called consistent and they can have infinitely many solutions.

Coincident lines Example

Go through the example given below to understand how to use the formula of coincident lines.

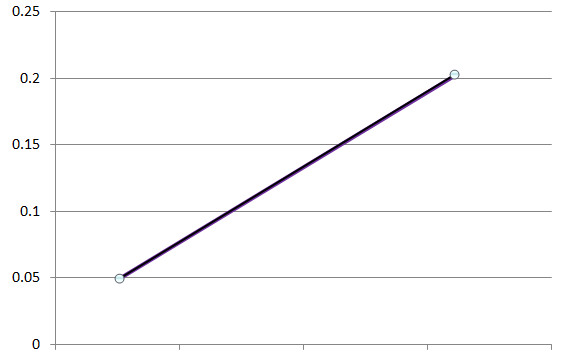
Example: Check whether the lines representing the pair of equations 9x – 2y + 16 = 0 and 18x – 4y + 32 = 0 are coincident.

Solution:

Given,

9x – 2y + 16 = 0
18x – 4y + 32 = 0

Comapring the above equations with a₁x + b₁y + c₁ = 0 and a₂x + b₂y + c₂ = 0,

a₁ = 9, b₁ = -2, c₁ = 16

a₂ = 18, b₂ = -4, c₂ = 32

Now,

a₁/a₂ = 9/18 = 1/2

b₁/b₂ = -2/-4 = 1/2

c₁/c₂ = 16/32 = 1/2

⇒ a₁/a₂ = b₁/b₂ = c₁/c₂

Therefore, the lines representing the given equations are coincident.

This can be shown graphically as:

To learn more about lines and their properties, visit www.byjus.com. Also, download BYJU’S – The Learning App today!