In decimal to binary conversion, we convert a base 10 number to a base 2 number by using simple methods. For example, if 1210 is a decimal number then its equivalent binary number is 11002. Thus, it is easy to convert the given decimal to binary using simple tricks which you will learn here. Students can learn here to convert any given decimal number into its equivalent binary number system using an online converter. In the number system, you may have learned about different types of numbers such as;
- Binary Numbers – Base 2
- Octal Numbers – Base 8
- Decimal Numbers – Base 10
- Hexadecimal Numbers – Base 16
These numbers can be converted from one system to other systems like decimal to binary, decimal to hex, decimal to octal and vice versa. In this article, you are going to learn the conversion of decimal to binary number systems along with the conversion steps and examples.

Table of Contents:
Decimal to Binary Conversion
A decimal number has base 10 and a binary number has base 2. In decimal to binary conversion, the base of the number also changes, i.e. from base 10 to base 2. All the decimal numbers have their equivalent binary numbers. These binary numbers are majorly used in computer applications, where it is used for programming or coding purposes. This is because computers understand the language of binary digits, o and 1.
Also, read: Decimal To Binary Converter
Let’s start with a basic understanding of the decimal and binary number systems before moving on to decimal to binary conversion.
Decimal Number System Definition
The decimal number system employs 10 symbols to represent numbers with a base of ten: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. It’s also known as the Hindu-Arabic number system, because each digit has a specific location and is ten times more significant than the one before it. 2130, 2850, and so on are examples of decimal numbers. It is the most widely used number system, with numbers that can be easily identified even if the base is not stated. In other words, if a number’s base is not written, it is regarded as a decimal number.
Binary Number System Definition
The binary number system is a base-2 number system in which numbers are only represented by two digits: 0 and 1. A bit is an abbreviated form of ‘binary digit,’ which is the smallest unit of data in a computer. A bit has only one binary value: either 1 or 0. It’s important to note that the Most Significant Bit (MSB) is the bit on the far left end of a binary number, while the Least Significant Bit (LSB) is the bit on the far right end (LSB). 11102, 10012, etc are examples of binary numbers.
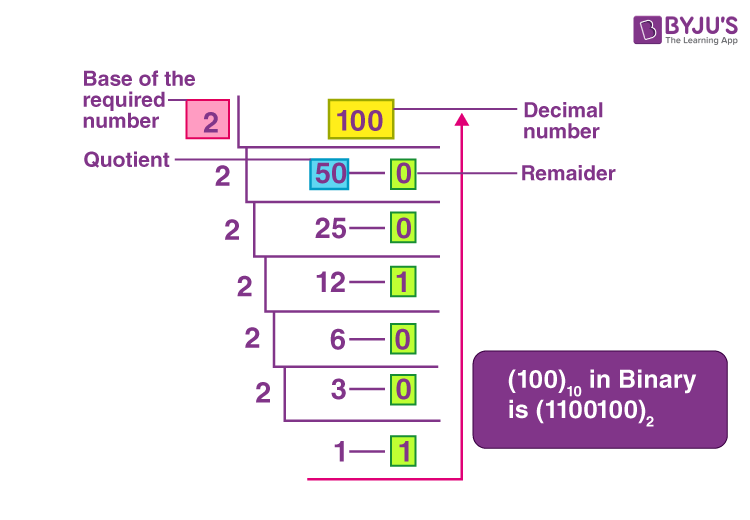
The above figure shows the conversion of a decimal number 100 to binary.
How to Convert Decimal Numbers to Binary Numbers?
We can convert the given decimal to binary using different methods such as formula, division method, and so on. In the section, you will learn how to convert decimal numbers to binary in the division method. To convert decimal to binary numbers, proceed with the steps given below:
Step 1: Divide the given decimal number by “2” where it gives the result along with the remainder.
Step 2: If the given decimal number is even, then the result will be whole and it gives the remainder “0”
Step 3: If the given decimal number is odd, then the result is not divided properly and it gives the remainder “1”.
Step 4: By placing all the remainders in order in such a way, the Least Significant Bit (LSB) at the top and Most Significant Bit (MSB) at the bottom, the required binary number will be obtained.
Now, let us convert the given decimal number 294 into a binary number.
| Divide by 2 | Result | Remainder | Binary Value |
| 294 ÷ 2 | 147 | 0 | 0 (LSB) |
| 147 ÷ 2 | 73 | 1 | 1 |
| 73 ÷ 2 | 36 | 1 | 1 |
| 36 ÷ 2 | 18 | 0 | 0 |
| 18 ÷ 2 | 9 | 0 | 0 |
| 9 ÷ 2 | 4 | 1 | 1 |
| 4 ÷ 2 | 2 | 0 | 0 |
| 2 ÷ 2 | 1 | 0 | 0 |
| 1 ÷ 2 | 0 | 1 | 1 (MSB) |
Therefore, the binary equivalent for the given decimal number 29410 is 1001001102
29410 =1001001102
Now, let us consider another example.
Convert 2 in Binary
2 in binary is 102. The number 2 represents 210, which is a decimal number. We know that the binary number system uses only two digits, such as 0 and 1. Hence, to convert 2 in a binary number system, follow the below steps.
Step 1: Divide 2 by 2. The integer quotient obtained in this step is used as a dividend for the next step. Continue this process until we get the quotient becomes 0.
|
Dividend |
Remainder |
|
2/2 = 1 |
0 |
|
1/2 = 0 |
1 |
Step 2: Now, write the remainder in reverse chronological order (i.e.) from bottom to top.
Hence, the decimal number 2 in binary is 102.
How to convert 3 in Binary?
3 in binary is given by 112. To convert decimal number 3, into a binary number, follow the steps below:
Step 1: Divide 3 by 2, then quotient will be 1 and the remainder left will be 1
Step 2: Divide 1 by 2, then the quotient will be o and the remainder will be 1.
Step 3: Take the remainders from LSB to MSB (bottom to top)in reverse order to get an equivalent binary number,
Decimal to Binary Table
To convert numbers from decimal to binary number system, you should remember the decimal to the binary table to solve the problems efficiently with an accurate solution. The decimal to binary conversion up to 20 numbers is given below for reference.
| Decimal Number | Binary Number |
| 0 | 0 |
| 1 | 1 |
| 2 | 10 |
| 3 | 11 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
| 8 | 1000 |
| 9 | 1001 |
| 10 | 1010 |
| 11 | 1011 |
| 12 | 1100 |
| 13 | 1101 |
| 14 | 1110 |
| 15 | 1111 |
| 16 | 10000 |
| 17 | 10001 |
| 18 | 10010 |
| 19 | 10011 |
| 20 | 10100 |
Related Articles
Decimal to Binary Examples
Example 1:
Convert 16010 to binary Number
Solution:
Given: Decimal Number = 16010
| Divide by 2 | Result | Remainder | Binary Value |
| 160 ÷ 2 | 80 | 0 | 0 (LSB) |
| 80 ÷ 2 | 40 | 0 | 0 |
| 40 ÷ 2 | 20 | 0 | 0 |
| 20 ÷ 2 | 10 | 0 | 0 |
| 10 ÷ 2 | 5 | 0 | 0 |
| 5 ÷ 2 | 2 | 1 | 1 |
| 2 ÷ 2 | 1 | 0 | 0 |
| 1 ÷ 2 | 0 | 1 | 1 (MSB) |
Therefore, 16010 = 101000002
Example 2:
Convert 1710 into a binary number
Solution:
Given: Decimal Number = 1710
| Divide by 2 | Result | Remainder | Binary Value |
| 17 ÷ 2 | 8 | 1 | 1 (LSB) |
| 8 ÷ 2 | 4 | 0 | 0 |
| 4 ÷ 2 | 2 | 0 | 0 |
| 2 ÷ 2 | 1 | 0 | 0 |
| 1 ÷ 2 | 0 | 1 | 1 (MSB) |
Therefore, 1710 = 100012
Let’s have a look at the conversion of a decimal number with fractional part to binary.
Question:
Convert 195.25 into binary.
Solution:
195 / 2 = 97 with remainder 1
97 / 2 = 48 with remainder 1
48 / 2 = 24 with remainder 0
24 / 2 = 12 with remainder 0
12 / 2 = 6 with remainder 0
6 / 2 = 3 with remainder 0
3 / 2 = 1 with remainder 1
1 / 2 = 0 with remainder 1
Thus, the binary equivalent of 195 is 11000011.
Now, we have to convert the fractional part of the given number into binary.
Multiply 0.25 by 2 and observe the resulting integer and fractional parts. Renew multiplying the resultant fractional part by 2 until we get a resulting fractional part equal to zero.
Then we need to write the integer parts from the results of each multiplication to make the equivalent binary number.
0.25 × 2 = 0 + 0.5
0.5 × 2 = 1 + 0
Here, 0.25 is equivalent to the binary number 0.01.
Therefore, (195.25)10 = (11000011.01)2
Decimal to Binary Practice Problems
Here are a few questions that are given for students, so that they can solve them and get good practice. Solving these problems will help students to increase their speed and attain good marks in the exams.
- Convert 24410 to its equivalent binary number.
- Convert 7610 to binary number.
- What is the binary equivalent of decimal number 89110?
- Convert 5710 into a binary number.
Register with BYJU’S – The Learning App to experience advanced learning methods with the help of personalised videos.

Frequently Asked Questions on Decimal to Binary
How do you convert decimal to binary?
Step 1: Divide the given decimal number by “2” to provide the result and the remainder.
Step 2: If the given decimal number is even, then the result will be whole, and it provides the remainder with “0”
Step 3: If the given decimal number is odd, the result is not divided correctly and provides the remainder with “1”.
Step 4: By placing all the remainders in order in such a way, the Least Significant Bit (LSB) at the top and Most Significant Bit (MSB) at the bottom, the required binary number will be obtained.
How do you convert 0.75 to binary?
0.75 × 2 = 1 + 0.5
0.5 × 2 = 1 + 0
Therefore, the binary equivalent of 0.75 is 0.11.
What is 10 in decimal to binary?
10 / 2 = 5 with remainder 0
5 / 2 = 2 with remainder 1
2 / 2 = 1 with remainder 0
1 / 2 = 0 with remainder 1
Therefore, the 10 in decimal is equal to 1010 in binary.
What is the value of 34 decimal to binary?
34 / 2 = 17 with remainder 0
17 / 2 = 8 with remainder 1
8 / 2 = 4 with remainder 0
4 / 2 = 2 with remainder 0
2 / 2 = 1 with remainder 0
1 / 2 = 0 with remainder 1
Hence, the decimal number 34 in binary is 100010.
What is the binary of 55?
55 / 2 = 27 with remainder 1
27 / 2 = 13 with remainder 1
13 / 2 = 6 with remainder 1
6 / 2 = 3 with remainder 0
3 / 2 = 1 with remainder 1
1 / 2 = 0 with remainder 1
Hence, the decimal number 55 in binary is 110111.

