The determinant of a matrix is the scalar value computed for a given square matrix. Linear algebra deals with the determinant, it is computed using the elements of a square matrix. It can be considered as the scaling factor for the transformation of a matrix. Useful in solving a system of linear equation, calculating the inverse of a matrix and calculus operations.
Geometrically, the determinant is seen as the volume scaling factor of the linear transformation defined by the matrix. It is also expressed as the volume of the n-dimensional parallelepiped crossed by the column or row vectors of the matrix. The determinant is positive or negative as per the linear mapping preserves or changes the orientation of n-space.
Definition of Determinant of Matrix
The determinant of a matrix is the scalar value or number calculated using a square matrix. The square matrix could be 2×2, 3×3, 4×4, or any type, such as n × n, where the number of column and rows are equal. If S is the set of square matrices, R is the set of numbers (real or complex) and f : S → R is defined by f (A) = k, where A ∈ S and k ∈ R, then f (A) is called the determinant of A.
Symbol
The determinant of a matrix is represented by two vertical lines or simply by writing det and writing the matrix name. eg. |A|, det(A), det A
Also, read:
Calculating the Determinant
To find a Determinant of a matrix, for every square matrix [A]nxn there exists a determinant to the matrix such that it represents a unique value given by applying some determinant finding techniques.
For 2 x 2 Matrix
For a 2 × 2 matrix the determinant can be represented as Δ
a_{11} & a_{12}\cr
a_{21} & a_{22}
\end{bmatrix}\end{array} \)
Note down the difference between the representation of a matrix and a determinant. In the case of a matrix, we enclose the value in a square bracket whereas in case of a determinant we enclose it in between two lines.
Determinant of 1 × 1 matrix
If [A] = [a] then its determinant is given as |a| which is equal to the value enclosed in the matrix.
The value of thedeterminant of a 2 × 2 matrix can be given as
det A =
Let us take an example to understand this very clearly,
Example 1: The matrix is given by, A =
3 & -1\cr
4 & 3
\end{bmatrix}\end{array} \)
Solution: We know the determinant can be calculated as:
|A| = (3 × 3) – (-1 × 4 )
|A| = 13
Thus, the value of the determinant of a matrix is a unique value in nature.
Minor of determinant
The sub matrices
a_{22} & a_{23}\cr
a_{32} & a_{33}
\end{bmatrix} \end{array} \)
a_{21} & a_{23}\cr
a_{31} & a_{33}
\end{bmatrix} \end{array} \)
a_{21} & a_{22}\cr
a_{31} & a_{32}
\end{bmatrix} \end{array} \)
The minor
⇒ det A =
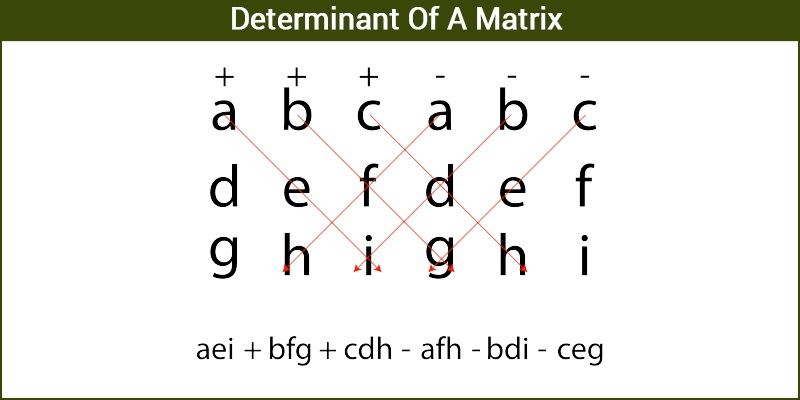
For 3 x 3 Matrix
The determinant of a 3 × 3 matrix is written as
det A =
a_{11} & a_{12} & a_{13}\cr
a_{21} & a_{22} & a_{23} \cr
a_{31} & a_{32} & a_{33}
\end{matrix}\right|\end{array} \)
The value of the determinant can be found out by expansion of the matrix along any row.
det A =
a_{22} & a_{23}\cr
a_{32} & a_{33}
\end{bmatrix} \end{array} \)
a_{21} & a_{23}\cr
a_{31} & a_{33}
\end{bmatrix} \end{array} \)
a_{21} & a_{22}\cr
a_{31} & a_{32}
\end{bmatrix} \end{array} \)
Let us see an example to find out the determinant of a 3 × 3 matrix,
Example 2: The matrix is given by, A =
4 & -3 & 5\cr
1 & 0 & 3\cr
-1 & 5 & 2
\end{bmatrix} \end{array} \)
Solution: To find the determinant of [A], let us expand the determinant along row 1.
Therefore, det A =
⇒ |A| = 4
0 & 3\cr
5 & 2
\end{matrix} \right|\end{array} \)
1 & 3\cr
-1 & 2
\end{matrix} \right|\end{array} \)
1 & 0\cr
-1 & 5
\end{matrix} \right|\end{array} \)
⇒ |A| = 4 (0 – 15) + 3(2+3) + 5(5-0) ⇒ |A| = -20
Hence, the determinant of a 3 × 3 matrix has a unique value.
It should be noted that the determinant is tried to be expanded along the row which has the maximum number of zeroes to make the calculations easy.
We have learned what determinants are and how to find the determinant of a given matrix. Please visit us at BYJU’S to learn more about determinants and other concepts. We make learning a unique experience for you same as every determinant has a unique value.
Comments