In Maths, the Fibonacci numbers are the numbers ordered in a distinct Fibonacci sequence. These numbers were introduced to represent the positive numbers in a sequence, which follows a defined pattern. The list of the numbers in the Fibonacci series is represented by the recurrence relation: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ……..,∞. In this article, let us discuss what is a Fibonacci number, properties, Fibonacci formulas and series in detail.
| Also, read: |
What is Fibonacci Number?
A Fibonacci number is a series of numbers in which each Fibonacci number is obtained by adding the two preceding numbers. It means that the next number in the series is the addition of two previous numbers. Let the first two numbers in the series be taken as 0 and 1. By adding 0 and 1, we get the third number as 1. Then by adding the second and the third number (i.e) 1 and 1, we get the fourth number as 2, and similarly, the process goes on. Thus, we get the Fibonacci series as 0, 1, 1, 2, 3, 5, 8, ……. Hence, the obtained series is called the Fibonacci number series.
We can also obtain the Fibonacci numbers from the pascal’s triangle as shown in the below figure.
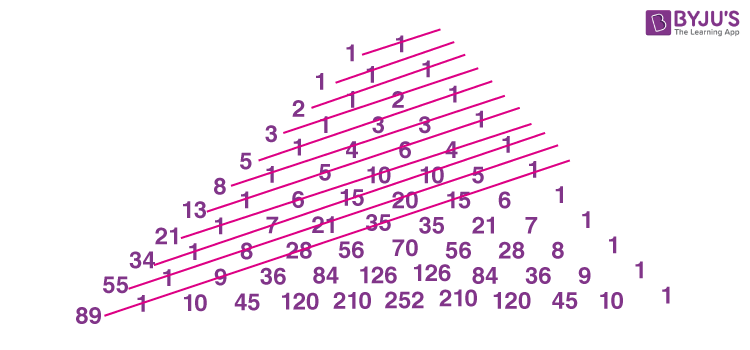
Here, the sum of diagonal elements represents the Fibonacci sequence, denoted by colour lines.
Fibonacci Series List
The list of numbers of Fibonacci Sequence is given below. This list is formed by using the formula, which is mentioned in the above definition.

Fibonacci Numbers Formula
The sequence of Fibonacci numbers can be defined as:
Fn = Fn-1 + Fn-2
Where Fn is the nth term or number
Fn-1 is the (n-1)th term
Fn-2 is the (n-2)th term
From the equation, we can summarize the definition as, the next number in the sequence, is the sum of the previous two numbers present in the sequence, starting from 0 and 1. Let us create a table to find the next term of the Fibonacci sequence, using the formula.
| Fn-1 | Fn-2 | Fn |
| 0 | 1 | 1 |
| 1 | 1 | 2 |
| 1 | 2 | 3 |
| 2 | 3 | 5 |
| 3 | 5 | 8 |
| 5 | 8 | 13 |
| 8 | 13 | 21 |
| 13 | 21 | 34 |
| 21 | 34 | 55 |
| 34 | 55 | 89 |
In the above table, you can see the numbers in each column are relational and diagonally the numbers are the same in all the three columns.

Fibonacci Number Properties
The following are the properties of the Fibonacci numbers.
- In the Fibonacci series, take any three consecutive numbers and add those numbers. When you divide the result by 2, you will get the three numbers. For example, take 3 consecutive numbers such as 1, 2, 3. when you add these numbers, i.e. 1+ 2+ 3 = 6. When 6 is divided by 2, the result is 3, which is 3.
- Take four consecutive numbers other than “0” in the Fibonacci series. Multiply the outer number and also multiply the inner number. When you subtract these numbers, you will get the difference “1”. For example, take 4 consecutive numbers such as 2, 3, 5, 8. Multiply the outer numbers, i.e. 2(8) and multiply the inner number, i.e. 3(5). Now subtract these two numbers, i.e. 16-15 =1. Thus, the difference is 1.
Fibonacci Numbers Examples
Question 1:
Write the first 6 Fibonacci numbers starting from 0 and 1.
Solution:
As we know, the formula for Fibonacci sequence is;
Fn = Fn-1 + Fn-2
Since the first term and second term are known to us, i.e. 0 and 1. Thus,
F0 = 0 and F1 = 1
Hence,
Third term, F2 = F0 + F1 = 0+1 = 1
Fourth term, F3 = F2+F1 = 1 + 1 = 2
Fifth term, F4 = F3+F2 = 1+2 = 3
Sixth term, F5 = F4+F3 = 3 + 2 = 5
So, the first six terms of Fibonacci sequence is 0,1,1,2,3,5.
Question 2:
Find the next term of Fibonacci series: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34.
Solution:
Each next term of the Fibonacci series is the sum of the previous two terms.
Therefore, the required term is;
21 + 34 = 55
Watch the Below Video to understand the Fibonacci Numbers and Golden Ratio

To learn more important mathematical concepts, please download BYJU’S -The Learning App and watch more interesting videos.
Frequently Asked Questions – FAQs
What are the first 10 Fibonacci numbers?
1, 1, 2, 3, 5, 8, 13, 21, 34, and 55
What are the numbers in the Fibonacci sequence?
What are Fibonacci numbers used for?
What are the first 12 Fibonacci numbers?
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, and 144
What is the 100th Fibonacci number?
We can find this number using the Fibonacci sequence formula.
