Linear equations in two variables class 9 questions are provided here for students to understand the concept very well as well as to get good grades in the final examinations. As a complete explanation is given for each question, students can find these questions useful to score good marks. Linear equations in two variables class 9 questions are framed as per the CBSE and NCERT curriculum. We have also provided practice problems for the students so that students can improve their problem-solving capabilities. To learn more about linear equations in two variables class 9, click here.
|
Linear Equations in Two Variables Class 9: In Linear equations in two variables class 9, students can learn different concepts such as introduction to a linear equation in one variable, a linear equation in two variables, process of finding the solution to the given linear equations, graphing methods and so on. Also, read: Linear Equations. |
Linear Equations in Two variables Class 9 Questions with Solutions
|
Linear Equation in Two Variables Definition: An equation is said to be a linear equation in two variables if it has two variables with degree one. The standard form for linear equation two variables is given by: Ax + By + C = 0, Where A, B and C are real numbers. Also, A and B should not be equal to 0. x and y are variables. Also, read: Linear Equation in One Variable. |
1. Write the linear equation 3x = -7y in the form Ax + By + C = 0 and determine the value of A, B and C.
Solution:
Given equation: 3x = -7y
As we know, the standard form of linear equation in two variables is Ax + By + C = 0
Thus, the given equation is written as:
3x + 7y + 0 = 0
Now, compare the above equation with the standard form, we get
A = 3, B = 7 and C = 0.
2. Determine the value of p, if (2, 0) is the solution of the linear equation 2x + 3y = p.
Solution:
Given linear equation: 2x + 3y = p
Now, substitute x = 2 and y = 0 in the given linear equation, we get
2(2) + 3(0) = p
4 + 0 = p
p = 4.
Therefore, the value of p is 4.
3. Give three solutions for the linear equation x = 4y.
Solution:
To determine three solutions for the linear equation x = 4y, substitute different values for the variables x and y.
If x = 0, then 0 = 4y
⇒ y = 0
If x = 1, then 1 = 4y
⇒ y = ¼
If x = 2, then 2 = 4y
⇒ y = 2/4 = 1/2
Therefore, we get
|
x |
0 |
1 |
2 |
|
y |
0 |
1/4 |
1/2 |
Therefore, the three solutions for x = 4y are (0, 0), (1, ¼) and (1, ½).
4. The cost of a pen is Rs. 5 less than half the cost of the notebook. Express the given statement in the form of a linear equation in two variables.
Solution:
Let the cost of the pen be x and the cost of the notebook be y.
According to the given condition, we can write
x = (½)y – 5
Now, the above equation can be written as:
x = (y/2) – 5
2x = y – 10
Rearranging the obtained equation, we get
2x – y + 10 = 0, which is the required linear equation in two variables.
5. Determine the point “P” if the graph of linear equation 2x + 3y = 6 cuts the Y-axis.
Solution:
Given linear equations: 2x + 3y = 6
As we know, if the graph of the linear equation cuts the y-axis, then the x – coordinate should be 0.
Thus, substituting x = 0 in the given linear equation,we get
2(0) + 3(y) = 6
0 + 3y = 6
3y = 6
y = 6/3
y = 2
Therefore, the point P = (0, 2)
Hence, the graph of linear equation 2x + 3y = 6 cuts the Y-axis at the point (0, 2).
6. Is (0, 2) is the solution of a linear equation x – 2y = 4.
Solution:
Given linear equation: x – 2y = 4
Now, substitute x = 0 and y = 2 in the given equation.
⇒ 0 – 2(2) = 4
⇒ – 4 ≠ 4
Therefore, (0, 2) is not a solution of a linear equation x – 2y = 4.
7. Write the equation 5x = 7/2 in the form of a linear equation in two variables.
Solution:
The equation 5x = 7/2 in the linear equation in two variables is:
5x + 0y – (7/2) = 0
The above obtained equation can also be written as:
10x + 0y – 7 = 0
8. Determine the solution for the linear equation.
Solution:
The linear equation 2x – 5y = 7 has infinitely many solutions.
Explanation:
Given equation: 2x – 5y = 7.
Thus, the equation can be written as follows:
-5y = 7 – 2x
y = -(7-2x) / 5
So, we get different “y” values if we use different “x” values.
Hence, we can conclude that the linear equation 2x – 5y = 7 has infinitely many solutions.
9. How to express the equation x = 9 in the form of a linear equation in two variables?
Solution:
Given equation: x = 9
It can also be written as x – 9 = 0
The standard form of linear equation in two variables is Ax + By + C = 0
Now, comparing the given equation and the standard form, we get
A = 1, B = 0 and C = -9.
Thus, the equation x = 9 in the form of linear equation in two variables is written as:
1x + 0y – 9 = 0
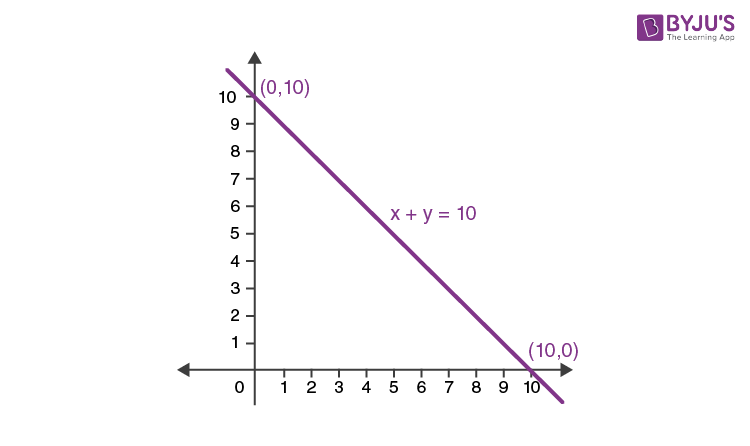
10. Draw the linear equation graph, given that the solutions are represented using the points in which the sum of the coordinates equals 10
Solution:
According to the given condition, we can write:
x + y = 10
Hence, y = 10 – x.
Now, let us randomly assume few values:
If x = 0, then y = 10 – 0 = 10
⇒ (0, 10)
If x = 5. Then y = 10 – 5 = 5
⇒ (5, 5)
If x = 10, then y = 10 – 10 = 0
⇒ (10, 0)
Now, plot the values (0, 10), (5, 5) and (10, 0) in the graph, we get the graph of the linear equation x + y = 10.
Explore More Articles:
- Functions Questions
- Numbers Questions
- Exponents and Powers Class 9 Questions
- Pair of Linear Equations in Two Variables Questions
- Linear Equations Questions
- Decimals Questions
- Rational Numbers Questions
Practice Questions
Answer the following:
- Check whether the given statement is true or false: (0, 3) is the solution of the linear equation 3x + 4y = 12.
- Prove that the points P(1, 2), Q(-1, -16), R(0, -7) lie on the graph of equation y = 9x – 7.
- Identify four solutions of the linear equation: x + πy = 4.
Download BYJU’S – The Learning App today to learn all Maths-related topics and also watch many engaging videos.