A vector relates two given points. It is a mathematical quantity having both the Magnitude and the direction.

Multiplication of Vectors

Multiplication of vectors can be of two types:

(i) Scalar Multiplication

(ii) Vector Multiplication

Here, we will discuss only the Scalar Multiplication by

Multiplication of vectors with scalar:

When a vector is multiplied by a scalar quantity, then the magnitude of the vector changes in accordance with the magnitude of the scalar but the direction of the vector remains unchanged.

Suppose we have a vector

\begin{array}{l} \vec{a} \end{array}

, then if this vector is multiplied by a scalar quantity k then we get a new vector with magnitude as |

\begin{array}{l} \vec{k a} \end{array}

|and the direction remains same as the vector

\begin{array}{l} \vec{a} \end{array}

if k is positive and if k is negative then the direction of k becomes just opposite of the direction of vector

\begin{array}{l} \vec{a} \end{array}

Vector a

Now let us understand visually the scalar multiplication of the vector

Let us take the values of ‘k ‘to be = 2,3,-3,

\begin{array}{l} \frac{- 1}{2} \end{array}

and so on.

Scalar Multiplicaiton of Vectors

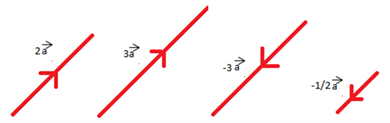
From the above-given set of vectors we see that the direction of vector

\begin{array}{l} \vec{a} \end{array}

remains same when the value of the scalar is positive and the direction becomes exactly opposite when the value of the scalar is negative and in both the cases the magnitude keeps changing depending upon the values of the scalar multiple.

As per above discussions we can see that

\begin{array}{l}  \end{array}

\begin{array}{l} \vec{k a} \end{array}

|=k|

\begin{array}{l} \vec{a} \end{array}

Suppose if the value of the scalar multiple k is -1 then by scalar multiplication we know that resultant vector is

\begin{array}{l} \vec{- a} \end{array}

, then

\begin{array}{l} \vec{a} \end{array}

+ (

\begin{array}{l} \vec{- a} \end{array}

) = 0. The vector

\begin{array}{l} \vec{- a} \end{array}

represents the negative or additive inverse of the vector

\begin{array}{l} \vec{a} \end{array}

Now suppose the value of k =

\begin{array}{l} \frac{1}{| a |} \end{array}

given that the value of

\begin{array}{l} \vec{a} \neq 0 \end{array}

then by the property of scalar multiple of vectors we have

\begin{array}{l} \vec{k a} \end{array}

= |k|

\begin{array}{l} \vec{a} \end{array}

\begin{array}{l} \frac{1}{| a |} \end{array}

× |

\begin{array}{l} \vec{- a} \end{array}

| .

Also, as per the above discussion, if k = 0 then the vector also becomes zero.

Let us go through an example to make this point more clear,

Example: A vector is represented in orthogonal system as

$\begin{array}{l} \vec{a} \end{array}$

=
$\begin{array}{l} 3 \hat{i} + \hat{j} + \hat{k} \end{array}$
. What would be the resultant vector if
$\begin{array}{l} \vec{a} \end{array}$
is multiplied by 5 ?

Solution: As the vector is to be multiplied by a scalar the resultant would be,

\begin{array}{l} \vec{a} \end{array}

= 5 (

\begin{array}{l} 3 \hat{i} + \hat{j} + \hat{k} \end{array}

)

\begin{array}{l} \vec{5 a} \end{array}

= (

\begin{array}{l} 15 \hat{i} + 5 \hat{j} + 5 \hat{k} \end{array}

)

To learn more about the multiplication of vectors, download BYJU’S – The Learning App.

Multiplication of Vectors

Multiplication of vectors with scalar:

Comments

Leave a Comment Cancel reply