Triangle Construction: Given its Perimeter and Two Angles

A triangle is a closed two-dimensional figure with three sides. There are different ways to construct a triangle. If the three sides are given, we can easily construct a triangle. Similarly, the construction of a triangle can be easily done when two sides – one included angle are given or two angles – one included side is given. In these cases, constructing a triangle is pretty easy. What if two angles and the perimeter of a triangle are given? Is it possible to construct the triangle? And the answer is Yes. Thus, in this article, we are going to discuss how to construct a triangle when its perimeter and its two angles are given.

How to Construct a Triangle When its perimeter and Two Angles are Given?

Below are the steps to construct a triangle ABC when its perimeter (i.e. AB + BC + CA) and two base angles B and C are given.

Given: The Perimeter (AB + BC + CA) of the triangle and two angles (i.e. ∠B and ∠C).

Requirements: A ruler, a protractor and a compass.

Steps of Construction:

Step 1: Draw a line segment XY such that XY = AB + BC + CA (i.e. perimeter of triangle ABC) and draw the angle lines at X and Y such that ∠LXY = ∠B and ∠MYX = ∠C.

Step 2: Draw the angle bisectors of ∠LXY and ∠MYX and let them meet at A.

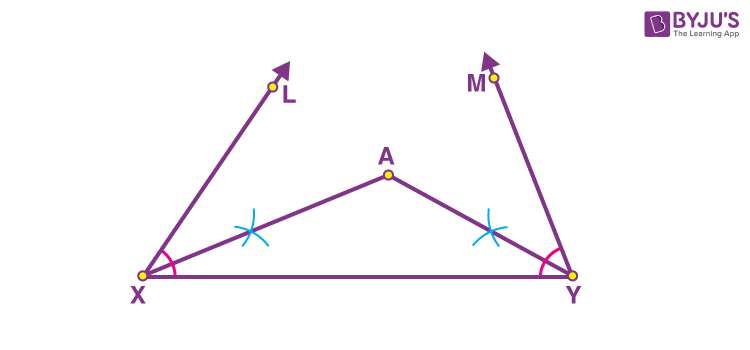
Step 3: Now, draw the perpendicular bisectors of AX and AY such that they intersect XY at B and C, respectively. Join AB and AC.

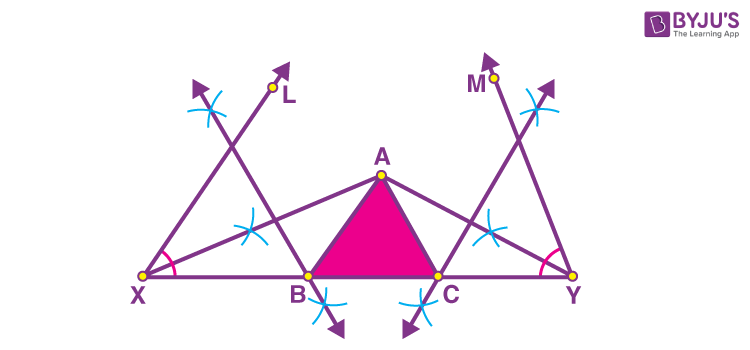
Hence, this is the required triangle ABC.

Example

Go through the example given below for a better understanding of the above construction steps.

Question: Let us consider a triangle ABC, whose perimeter is 15 cm and the two given angles are 55° and 60°. That means AB +BC + CA = 15 cm , ∠B = 55° and ∠C = 60°. Construct a triangle ABC with these measurements.

Solution:

Given,

AB + BC + CA = 15 cm (perimeter)

∠B = 55° and ∠C = 60°

The steps of construction are:

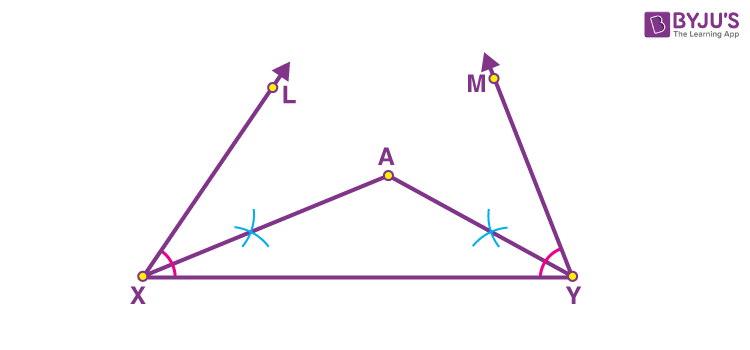
• Draw a line segment XY of length equal to AB + AC + BC, that is, 15 cm.
• From point X, using the protractor construct ∠LXY which is equal to ∠B, that is, 55°.
• From the point Y, construct ∠MYX which is equal to ∠C, that is, 60°.
• Using the compass, construct the bisectors of ∠LXY and ∠MYX. Mark the point as A where these bisectors meet.

• Construct the perpendicular bisector of AX and name it PQ.
• Construct the perpendicular bisector of AY and name it RS.
• Let PQ meet XY at B and RS meet XY at C.
• Join the points A and B as well as A and C.

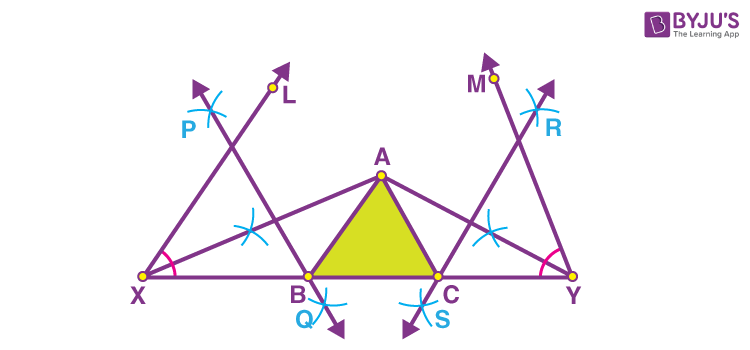
Hence, ∆ABC is the required triangle with the given measurements.

Video Lesson on Triangles