Numbers are found everywhere in Mathematics as well as in day to day life. There are different types of numbers in Mathematics. Prime numbers are one of the important ones. Let us discuss the definition of the prime number and the prime numbers up to 100 in this article.
Prime Numbers Definition
A prime number is a positive integer that is divisible by only 1 and itself. i.e. there is no number other than 1 and itself that divides a prime number.
| Also, read: |
Prime Number Properties
There are various properties that prime numbers possess. These properties are listed below:’
- Prime numbers are positive numbers greater than 1.
- For a number to be a prime number, it must be a non-zero whole number.
- Prime numbers are numbers that cannot be divided by any number except themselves and one.
- Prime numbers have only two factors.
- The two factors of prime numbers are one and the number itself.
- The way of finding the prime numbers is called integer factorization or prime factorization.
List of Prime Numbers Up to 100
The list of prime numbers 1 to 100 are given below:
| Prime Numbers from 1 to 100
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97. |
Prime Numbers Facts:
- The only even prime number is 2 and the remaining even numbers can be divided by 2. So, it can’t be a prime number.
- No prime number greater than 5 ends with a 5. Since any number greater than 5 that ends with a 5 can be divided by 5, it can’t be a prime number.
- Zero and 1 are not prime numbers.
- The numbers 0 and 1, are neither a prime numbers nor a composite numbers.
How to Find Prime Numbers up to 100?
The technique to find the prime numbers up to 100 is given below:
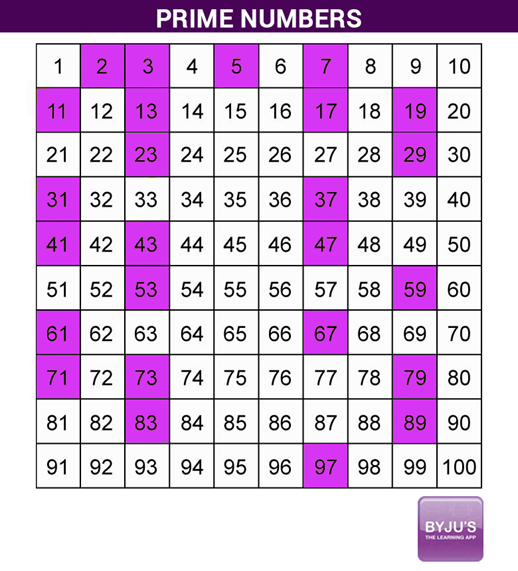
- Write out the numbers from 1 to 100 shown above
- Keep the number 1 as it is because all primes are greater than 1
- Number 2 is a prime, so highlight the number 2, and keep the numbers as it is which are multiples of 2. (such as 4, 6, 8,10, ….)
- The number 3 is a prime, so highlight the number 3, and keep the numbers as it is which are multiples of 3. (such as 6, 9, 12,15, ….)
- The next number left is 5, so highlight the number 5 and keep the numbers as it is which are multiples of 5 (such as 10, 15, 20, 25, …..)
- At the end, the number left in the first row is number 7, now highlight the number 7 and keep all the numbers that are multiples of 7 (such as 14, 21, 28, ……)
- Finally, all the leftover highlighted numbers in the table are prime numbers.
Video Lesson on Prime Numbers

Solved Questions on Prime Numbers
Question 1:
What is the average of the prime numbers between 1 to 10?
Solution:
Prime numbers between 1 to 10 are 2, 3, 5, 7
Numbers of prime numbers = 4
Average = (2 + 3 + 5 + 7)/4 = 17/4 = 4.25.
Question 2:
How many even integers between 2 and 20 can be represented as sum of two different prime numbers?
Solution:
Even integers between 2 and 20 are 4, 6, 8, 10, 12, 14, 16, 18. Then we have
| 4 | 2 + 2 |
| 6 | 1 + 5, 2 + 4, 3 + 3 |
| 8 | 1 + 7, 2 + 6, 3 + 5, 4 + 4 |
| 10 | 1 + 9, 2 + 8, 3 + 7, 4 + 6, 5 + 5 |
| 12 | 1 + 11, 2 + 10, 3 + 9, 4 + 8, 5 + 7, 6 + 6 |
| 14 | 1 + 13, 2 + 12, 3 + 11, 4 + 10, 5 + 9, 6 + 8, 7 + 7 |
| 16 | 1 + 15, 2 + 14, 3 + 13, 4 + 12, 5 + 11, 6 + 10, 7 + 9, 8 + 8 |
| 18 | 1 + 17, 2 + 16, 3 + 15, 4 + 14, 5 + 13, 6 + 12, 7 + 11, 8 + 10, 9 + 9 |
Therefore, the even integers between 2 and 20 which can be expressed as sum of two different prime numbers are 8, 10, 12, 14, 16, 18.
Question 3:
Find the next three numbers of the following sequence:
(i) 2, 3, 5, 7, …
(ii) 4, 5, 7, 9, …
(iii) 4, 9, 25, 49, …
Solution:
(i) Clearly, it is sequence of prime numbers,
∴ 11, 13, 17 are the next three terms.
(ii) 2 + 2 = 4
3 + 2 = 5
5 + 2 = 7…
The general rule of this sequence is that each consecutive prime number is added by 2
∴ 13, 15, and 19 are the next three terms.
(iii) 22 = 4, 32 = 9, 52 = 25, 72 = 49,..
∴ 121, 169, 289 are the next three terms.
Practice Questions
- If p is a prime number, then how many factors does p2 have?
- Find the average of the first 20 prime numbers.
- If the sum of four consecutive integers is 210. Which one of them is a prime number?
Stay tuned with BYJU’S – The Learning App and download the app to learn all Maths-related articles with ease.
Frequently Asked Questions on Prime Numbers Up to 100
What is the list of prime numbers from 1 to 100?
Prime numbers from 1 to 100 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
What are the first ten prime numbers?
The first ten prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29.
How many prime numbers are there from 1 to 100?
There are 25 prime numbers between 1 to 100 which are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
What is the average of first ten prime numbers?
The first ten prime numbers are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
Average = (2 + 3 + 5 + 7 + 11 + 13 + 17 + 19 + 23 + 29)/10 = 12.9.
