Do you know how to find prime numbers easily? This article covers the concept of finding prime numbers (both small and large) using factorization method. By the definition of a prime number, we know that the prime numbers have only two factors present in it. The two factors would be 1 and the original number itself. Hence, we need to find here the numbers which consist of only two factors. This is possible by using a simple method, which is called prime factorisation.
It is easy to find the primes for smaller numbers, but for larger numbers, we have to discover another way to find the primes. Hence, here we have explained to evaluate the prime numbers not only for smaller digits but also for bigger numbers. Here, students will also learn a shortcut way to find prime numbers from 1 to 100 using its chart.
| Table of Contents: |
Methods to Find Prime Numbers Easily
There are various methods to determine whether a number is prime or not. The best way for finding prime numbers is by factorisation method. By factorisation, the factors of a number are obtained and, thus, one can easily identify a prime number.
Finding Prime Numbers Using Factorization
Factorisation is the best way to find prime numbers. The steps involved in using the factorisation method are:
- Step 1: First find the factors of the given number
- Step 2: Check the number of factors of that number
- Step 3: If the number of factors is more than two, it is not a prime number.
Example: Take a number, say, 36.
Now, 36 can be written as 2 × 3 × 2 × 3. So, the factors of 36 here are 1, 2, 3, 4, 6, 9, 12, 18, and 36. Since the number of factors of 36 is more than 2, it is not a prime number but a composite number.
Now, if we take the example of 19. The prime factorisation of 19 is 1 x 19. You can see here, there are two factors of 19. Hence, it is a prime number.
How to Tell if a Large Number is Prime?
There are some Prime Number Formulas, which can be used to find the primes. To check whether a large number is a prime number or not, follow the steps given below:
- Step 1: Check the units place of that number. If it ends with 0, 2, 4, 6 and 8, it is not a prime number.
| Note: “Numbers ending with 0, 2, 4, 6 and 8 are never prime numbers.” |
- Step 2: Take the sum of the digits of that number. If the sum is divisible by 3, the number is not a prime number.
| Note: “Numbers whose sum of digits are divisible by 3 are never prime numbers.” |
- Step 3: After confirming the falsity of steps 1 and 2, find the square root of the given number.
- Step 4: Divide the given number by all the prime numbers below its square root value.
- Step 5: If the number is divisible by any of the prime numbers less than its square root, it is not a prime number; otherwise, it is prime.
Exception: If a large number is ending with 5, then it is always divisible by 5. Hence, it is not a prime number
Also, read:
| Is 1 a Prime Number? | Is 2 a Prime Number? |
| Is 91 a Prime Number? | Is 101 a Prime Number? |
Prime Numbers From 1 to 200
Here is a table for the ease of the students to check the prime numbers present between 1 and 200.
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 |
| 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 |
| 199 | ||||||||
Video Lesson on Numbers

Examples
Example 1:
- Take a number, say, 234256
- Since the unit digit of 234256 is 6, it is not a prime number.
Example 2:
- Take a number, say, 26577
- The unit digit of this number is not 0, 2, 4, 6 or 8
- Now, take the sum of digits which will be: 2 + 6 + 5 + 7 + 7 = 27
- Since 27 is divisible by 3, 26577 is not a prime number.
Example 3:
- Take another number, say, 2345
- Since, the number ends with 5, therefore, it is divisible by 5.
- 2345/5 = 469
- Hence, apart from 1 and 2345, 5 is also a factor.
- Therefore, 2345 is not a prime number
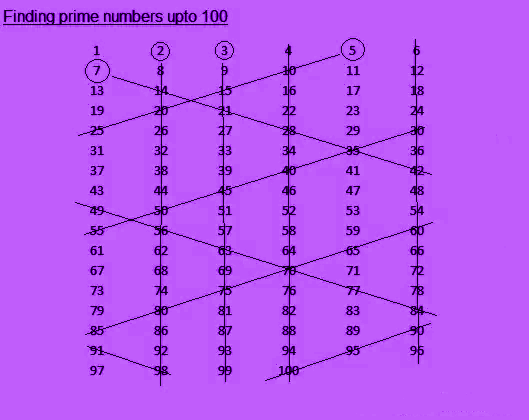
Shortcut to Find Prime Numbers
One of the shortcuts to finding the prime numbers are given below.
- Step 1: Write all the numbers from 1 to 100 with 6 numbers in a row (as shown in the figure).
- Step 2: As the square root of 100 is ±10, the multiples of numbers till 10 has to be crossed out.
- Step 3: Choose 2 and cross the entire column as all are multiple of 2. Also, cross out the entire columns of 4 and 6 as those are also 2’s multiples.
- Step 4: Now move to 3 and cross out the entire column.
- Step 5: Take 5 and cross out the diagonally towards left. Then, cross out diagonally from numbers 30, 60, and 90. Now, all the multiples of 5 are crossed out.
- Step 6: Choose 7 and cross out diagonally towards the right. Then, check the next number on that column which is divisible by 7 and cross diagonally right. The first number on that column that is divisible by 7 is 49 and then 91. Crossing diagonally right from 49 to 91 leaves no multiples of 7 on the list.
Now, the remaining numbers on this list are prime numbers. The image below shows this list.
Some Important Points about Prime Numbers
- ‘2’ is the only prime number which is even, rest all other primes are odd numbers.
- ‘2’ and ‘3’ are the only two consecutive prime numbers
- All even numbers greater than 2 can be represented as the sum of two prime numbers.
Keep visiting BYJU’S for more such maths lessons. Also, download BYJU’S- The Learning App to get video lessons on different maths topics and learn in an engaging, effective and personalized way.
Frequently Asked Questions
What is the smallest even prime number?
2 is the only even prime number.
How do you know a prime number?
If a number has only two factors 1 and itself, then the number is prime. Hence, by prime factorisation of the given number, we can easily determine a prime number.
Why 11 is a prime number?
The prime factorisation of 11 is 1 × 11 since 11 has only two factors 1 and itself, hence it is a prime number.
What are the prime numbers from 1 to 50?
The prime numbers from 1 to 50 are 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47.
Is 101 a prime number?
Yes, 101 is a prime number.


I want to learn PS