Rational and Irrational numbers both are real numbers but different with respect to their properties. A rational number is the one which can be represented in the form of P/Q where P and Q are integers and Q ≠ 0. But an irrational number cannot be written in the form of simple fractions. ⅔ is an example of a rational number whereas √2 is an irrational number.
Let us learn more here with examples and the difference between them.
| Table of contents: |
Definitions
What is a Rational number?
Rational numbers are numbers which can be expressed as a fraction and also as positive numbers, negative numbers and zero. It can be written as p/q, where q is not equal to zero.
The word “rational” is derived from the word ‘ratio’, which actually means a comparison of two or more values or integer numbers and is known as a fraction. In simple words, it is the ratio of two integers.
Example: 3/2 is a rational number. It means integer 3 is divided by another integer 2.
Get more information about rational numbers here.
What is an Irrational Number?
The numbers which are not rational numbers are called irrational numbers. Now, let us elaborate, irrational numbers could be written in decimals but not in the form of fractions, which means they cannot be written as the ratio of two integers.
Irrational numbers have endless non-repeating digits after the decimal point. Below is an example of an irrational number:
How to Classify Rational and Irrational Numbers?
Let us see how to identify rational and irrational numbers based on the given set of examples.
As per the definition, rational numbers include all integers, fractions and repeating decimals. For every rational number, we can write them in the form of p/q, where p and q are integer values.
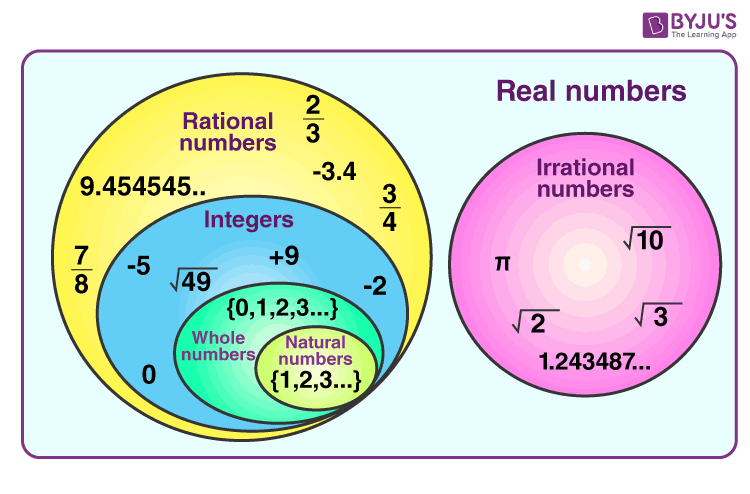
Venn Diagram
The below image shows the Venn diagram of rational and irrational numbers which come under real numbers.
Difference Between Rational and Irrational Numbers
| Rational Numbers |
Irrational Numbers |
| It is expressed in the ratio, where both numerator and denominator are the whole numbers | It is impossible to express irrational numbers as fractions or in a ratio of two integers |
| It includes perfect squares | It includes surds |
| The decimal expansion for rational numbers executes finite or recurring decimals | Here, non-terminating and non-recurring decimals are executed |
Also, read: Difference Between Rational Numbers And Irrational Numbers
Examples
A list of examples of rational and irrational numbers is given here.
Examples of Rational Numbers
- Number 9 can be written as 9/1 where 9 and 1 both are integers.
- 0.5 can be written as ½, 5/10 or 10/20 and in the form of all termination decimals.
- √81 is a rational number, as it can be simplified to 9 and can be expressed as 9/1.
- 0.7777777 is recurring decimals and is a rational number
Examples of Irrational Numbers
Similarly, as we have already defined that irrational numbers cannot be expressed in fraction or ratio form, let us understand the concepts with a few examples.
- π is an irrational number that has a value of 3.142…and is a never-ending and non-repeating number.
- √2 is an irrational number, as it cannot be simplified.
- 0.212112111…is a rational number as it is non-recurring and non-terminating.
There are a lot more examples apart from the above-given examples, which differentiate rational numbers and irrational numbers.
Properties of Rational and Irrational Numbers
Here are some properties based on arithmetic operations such as addition and multiplication performed on the rational number and irrational number.
1: The sum of two rational numbers is also rational.
Example: 1/2 + 1/3 = (3+2)/6 = 5/6
2: The product of two rational numbers is rational.
Example: 1/2 x 1/3 = 1/6
3: The sum of two irrational numbers is not always irrational.
Example: √2+√2 = 2√2 is irrational
2+2√5+(-2√5) = 2 is rational
4: The product of two irrational numbers is not always irrational.
Example: √2 x √3 = √6 (Irrational)
√2 x √2 = √4 = 2 (Rational)
Video Lesson on Rational Numbers

Class Related Links
Solved Problems
Q.1: Find any 5 rational numbers between 5 and 6.
Solution:
We need to find 5 rational numbers between 5 and 6.
So, multiply and divide the numbers 5 and 6 by 5 + 1, i.e., 6.
That means, 5 = 5 × (6/6) = 30/6
6 × (6/6) = 36/6
Therefore, five rational numbers between 5 and 6 are 31/6, 32/6, 33/6, 34/6, and 35/6.
Q.2: Classify the following as rational and irrational numbers.
√12, √16, √5, 0.9444, 22/7, 1.23123123412…
Solution:
√12 = Irrational number
√16 = ±4 = Rational number
√5 = Irrational number
0.9444 = Rational number
22/7 = Rational number
1.23123123412… = Irrational number
Q.3: Is the square root of 144 a rational number?
Solution:
Yes, the square root of 144 is a rational number since √144 = ±12.
Practice Questions
- State whether the product of -2√3 and -2√5 is irrational.
- How do you find four rational numbers between 10 and 11?
- Explain why the product of two irrational numbers may or may not be a rational number using suitable examples.
Learn more maths topics and get related videos at BYJU’S- The Learning App.
Frequently Asked Questions – FAQs
What are rational and irrational numbers?
What is the difference between rational and irrational numerals?
Give examples of rational and irrational numbers.
Examples of irrational numbers are √2, √3, pi(π), etc.

I want to know about rational and irrational number
Question 5: In the following equation, find which variables x, y, z etc. represent rational or irrational numbers:
Rational and Irrational Numbers Examples
Please solve this question
Thank you byjus
You helped me with my projects
Is the sum of a rational and irrational number is rational and why?
The sum of a rational and irrational number is irrational.
As we know, an irrational number is a non-terminating and non-repeating decimal.
Therefore, any number added to an irrational number will result in an irrational number only.
You have said that “pi” is irrational in Venn diagram. But again in example questions, you are saying that 22/7 which is nothing but “pi” as Rational number.
Kindly explain.
The value of π is approximately equal to the number obtained by dividing 22 by 7. But the actual value of π is non-terminating and non-recurring, making it an irrational number. 22/7, however, is a rational number, which is in the form of p/q, and its decimal expansion is non-terminating & recurring.