To find the square root of 25, we can use both prime factorisation and the long division method. If we have the knowledge of squares from 1 to 10, we can also calculate the square root of 25 mentally. In radical form, the square root of 25 is written as √25, where the ‘√’ sign is called the radical sign. In exponential form, it is written as (25)½ or (25)0.5. To find the square root of 25, we have to find a number whose square is 25.
Learn more about square and square roots.
|
Square Root of 25 |
± 5 |
|
Square of 25 |
625 |
What is the Square Root of 25?
The square root of 25 is a number whose square is 25. Now, if we square both 5 and –5 we get the answer 25. Thus, the square root of 25 is both 5 and –5, we choose the positive or the negative root as per the requirement of the problem.
We can also express the square root of 25 as the roots of the quadratic equation x2 – 25 = 0
x2 – 25 = 0
⇒ x2 = 25 (taking square roots on both sides)
⇒ x = √25
⇒ x = ± 5
Check out the properties of perfect square numbers.
How to Find the Square Root of 25?
Let us find the square root of 25 using the prime factorisation and long division method. We can even calculate the square root if we remember the times table of 5.
Now, 25 = 5 × 5
∴ √25 = √(5 × 5) = 5.
Prime Factorisation Method
To find the square root of 25 by the prime factorisation method, we first prime factorise 25 and then make pairs of two to get the square root.
Prime factorisation of 25 = 5 × 5
Square root of 25 = √[5 × 5] = 5.
Repeated Subtraction Method
To find the square root by repeated subtraction method, we shall repeatedly subtract consecutive odd numbers from 25 till we get zero.
25 – 1 = 24
24 – 3 = 21
21 – 5 = 16
16 – 7 = 9
9 – 9 = 0
So, for the 5th odd number the difference is zero. Therefore, the square root of 25 is 5.
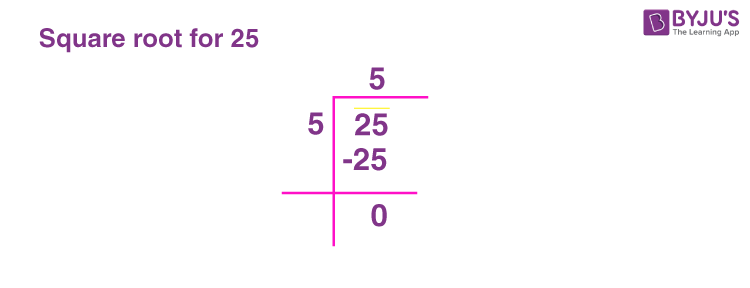
Long Division Method
The long division method is often not required to find the square root of 25. Let us see how to calculate the square root of 25:
Video Lessons on Square Roots
Visualising square roots

Finding Square roots

Related Articles
Solved Examples on Square Root of 25
Example 1:
Find the length of the hypotenuse of a right angled triangle if the sum of the squares of other two sides is 25 cm.
Solution:
Let ABC be the right-angled triangle, right-angled at B. Then,
AC = √(AB2 + BC2) = √25 (since the sum of the square of the perpendicular sides is 25 cm)
⇒ AC = 5 cm (taking the positive root as length cannot be negative)
Thus, the length of the hypotenuse of the triangle is 5 cm.
Example 2:
Find the smallest number that must be divided from 125 to make it a perfect square. Also, find the square root of the perfect square number.
Solution:
Prime factorisation of 125 = 5 × 5 × 5
On pairing, 5 is left out, hence 5 must be divided from 125 to make it a perfect square.
∴ 125 ÷ 5 = 25.
Square root of 25 = √25 = ± 5.
Example 3:
During a practice parade, 25 students were needed to stand in such a way that the number of students in one row is equal to the total number of rows. Find the total number of students in each row.
Solution:
Let there be x number of students in one row. Since the number of students in each row is equal to the number of rows.
Total number of students = x × x = x2 = 25
⇒ x = √25 = 5
∴ there are 5 students in one row.
Frequently Asked Questions on Square Root of 25
What is the square root of 25?
The square root of 25 is ± 5.
Is 25 a perfect square number?
Yes, 25 is a perfect square number as the square of ±5 is 25.
Is the square root of 25 rational or irrational?
The square root of 25 is a rational number.
What is the prime factorisation of 25?
The prime factorisation of 25 is 5 × 5.
What is the cube root of 25?
The cube root of 25 is 2.924 (approx.).
What is the square root of –25?
The square root of –25 is not a real number. It is an imaginary number. The square root of –25 = √( –1 × 25) = √(–1) × √25 = i × 25 = 25i. The quantity ‘i’ called iota is the imaginary unit number.