Square Root of 32

In Mathematics, the square root of 32 is a number, which when multiplied by itself results in the original number 32. The value of square root of 32 is an irrational number, as it cannot be expressed in the form of p/q. In this article, we are going to discuss two different methods such as the long division method and prime factorization method to find the square root of 32 in detail.

Table of Contents:

• What is the Square Root of 32?
• Square Root of 32 in Radical Form
• Square Root of 32 by Prime Factorization Method
• Square Root of 32 by Long Division Method
• Examples
• FAQs

What is the Square Root of 32?

The square of 32 is a number if it is multiplied by itself and gives the result as 32. The square root of 32 is symbolically expressed as √32.

Hence, √32 = √(Number × Number)

Thus, if we multiply the number 5.656 two times, we get the original value 32.

(i.e) √32 = √(5.656× 5.656)

√32 = √(5.656)²

Now, remove square and square root, we get

√32 = ± 5.656.

Square Root of 32 in Radical Form

The square root of 32 can also be expressed in the radical form. If we know the prime factorization of 32, we can write the simplest radical form of the square root of 32. Thus, the prime factorization of 32 is 2 × 2 × 2 × 2 × 2. If it is written in the radical form, then the simplest radical form of the square root of 32 is 4√2.

Square Root of 32 by Prime Factorization Method

To find the square root of 32 using the prime factorization method, first, write the prime factorization of 32. Thus, the prime factorization of 32 is 2 × 2 × 2 × 2 × 2.

Thus, √32 = (√2)². (√2)². √2

√32 = (2×2)×√2.

√32 = 4√2

We know that,

√2 = 1.414

Now, substitute the values of √2 in the above equation.

√32 = 4×1.414

√32 =5.656 (approximately)

Hence, the square root of 32 in decimal form is approximately equal to 5.656.

Square Root of 32 by Long Division Method

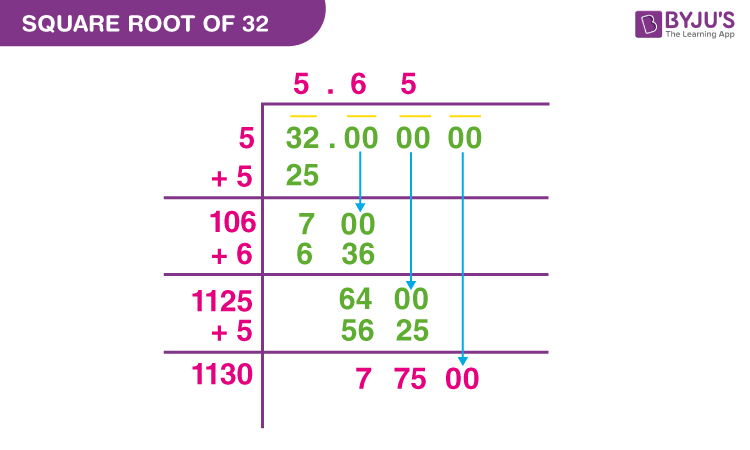
The procedure to find the square root of 32 using the long division method is given as follows:

Step 1: Write the number 32 in decimal form. To find the exact value of the square root of 32, add 6 zeros after the decimal point. Hence, 32 in decimal form is 32.000000. Now, pair the number 32 from right to left by putting the bar on the top of the number.

Step 2: Now, divide the number 32 by a number, such that the product of the same number should be less than or equal to 32. Thus, 5×5 =25, which is less than 32. Thus, we obtained the quotient = 5 and remainder = 7.

Step 3: Double the quotient value, so we get 10, and assume that 100 is the new divisor. Now, bring down the value 00 for division operation. So, the new dividend obtained is 700. Now, find the number, such that (100 + new number) × new number should give the product value, that should be less than or equal to 700. Hence, (100+6) × 6 = 636, which is less than 700.

Step 4: Now subtract 636 from 700, and we get 64 as the new reminder, and 56 as a quotient.

Step 5: The new quotient obtained is 56, and double that. Hence, we get 112 and assume that 1120 is our new divisor. Now, bring down the two zeros and, we have 6400 as the new dividend.

Step 6: Find the number, such that (1120 + new number) × new number should give the product value, that should be less than or equal to 6400. Thus, (1120+5)× 5 = 5625, which is less than 6400.

Step 7: Subtract 5625 from 6400, and we get 775 as the new reminder.

Step 8: Continue this process until we get the approximate value of the square root of 32 up to three decimal places. (Note: keep the decimal point in the quotient value after bringing down all the values in the dividend).

Step 9: Thus, the approximate value of the square root of 32, √32 is 5.656.

Video Lessons on Square Roots

Visualising square roots

Finding Square roots

Examples

Example 1:

Simplify 40 -√32.

Solution:

Given: 40 – √32.

We know that the square root of 32 is 5.656

Now, substitute the value in the expression, we get:

40 -√32 = 40 – 5.656

40 -√32 = 34. 344

Therefore, 40 -√32 is 34.344.

Example 2:

Simplify 4√32×√32.

Solution:

Given: 4√32×√32

We know that the square root of 32 in the simplest radical form is 4√2.

Now, substitute √32 = 4√2 in the given expression, we get

4√32×√32= 4(√32)²

4√32×√32 = 4(32)

4√32×√32 = 128 .

Hence, the simplified form of 4√32×√32 is 128.

Example 3:

Find the value of m, if m√32 +15 = 70.

Solution:

Given equation: m√32 +15 = 70…(1)

We know that √32 = 5.656.

Now, substitute the value in equation (1), we get

m(5.656) + 15 = 70

m(5.656) = 70-15

5.656m = 55

m = 55/5.656

m = 9.724

Therefore, the value of m is 9.724.