The MP Board Class 11th Maths Syllabus is an important document, same as any question papers or other class textbooks. Subject specialists create it based on the topics covered during the academic year and its subsections. The MP Board Syllabus for Class 11 Math will give everyone, from the parent to the student and teacher, a complete overview of the subject with the topics and sub-topics. This will help the students to know better if they need to prepare ahead for any particular area of Class 11 MP Board Maths.
The topics covered under the MP State Board Class 11 Syllabus for the mathematics include topics ranging from the sets, functions, algebra to geometry, calculus, mathematical reasoning and even statistics and probability. These main topics also further divided into different sub-topics. This syllabus helps a student and teacher to be on the same page as to what is covered in a subject during the year 2021-2022, thus acting more as an MP Board class guide for 11th standard.
MP Board Class 11 Maths Syllabus 2021-2022 PDF
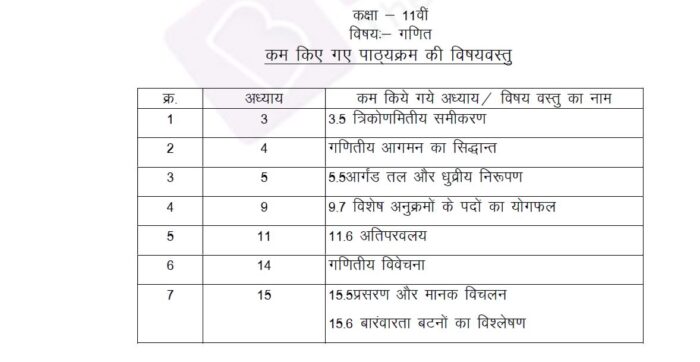
Find details of the chapter in Hindi, in the screenshot given below:
Is Madhya Pradesh State Board Class 11th Maths Syllabus important?
Obviously, yes! It will tell the students where they stand in any particular area of mathematics. Do they find one area more difficult than the other? How well do they know their Calculus or Algebra? Are they able to gauge where they stand on a particular area of Class 11 Mathematics?
All these questions and more will be answered to the students when they download the state board syllabus 2021-22 of Class 11 in MP. How? Because then they will get complete details of all the mathematical concepts and formulas that are covered in Class 11. Since the MP State Board Class 11 syllabus is a continuation of the concepts developed from earlier classes, it will help the students to know how to plan well so that they ace their exams.
For more details about the Class 11 Syllabus, pay a visit to our website.
For more details about MP Board and its resources tune into BYJU’S.

Comments