MPBSE 12th Maths Question Paper 2019 with Answers – Free Download
Madhya Pradesh Class 12 Maths 2019 question paper with solutions is available here in a downloadable pdf format and also in the text, so that the students will get an idea about the Maths marking scheme. Along with the solutions, maths question paper 2019 Class 12 is also added here for reference.
MPBSE 12th students will be able to access all the MPBSE 12th previous year maths question papers. The solutions provided by BYJU’S will instil confidence in the students to practise well and prepare for the exam to complete the paper in a designated time, which improves their writing speed and accuracy. It can be downloaded easily and in a shorter period of time, without any hassle.
Solving 2019 Maths question papers and also the previous year papers for Class 12 will enhance one’s preparation level by making students aware of the type of questions asked in the upcoming MPBSE board examinations.
Download MPBSE 12th Board Maths Question Paper in PDF 2019
Download Madhya Pradesh 12th Board Maths Paper in PDF 2020 With Solutions
MPBSE Class 12th Maths Question Paper With Solutions 2019
QUESTION PAPER CODE E – 236
SECTION – A
Question 1: Choose and write the correct options. 1* 5 = 5M
[i] Let A = {1, 2, 3}, then number of equivalence relations containing
(1, 2) is:
(A) l (B) 2 (C) 3 (D) 4
Solution: (B)
Total possible pairs = {(1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (3, 3)}
Reflexive means (a, a) must be in relation.
Hence (1, 1), (2, 2), (3, 3) must be in a relation.
Symmetric means if (a, b) is in relation, then (b, a) must be in relation.
Therefore, if (1, 2) is in relation, then (2, 1) must also be in relation.
Transitive means if (a, b) is in relation, and (b, c) is in relation, then (a, c) is in relation.
If (1, 2) is in relation, and (2, 1) is in relation, then (1, 1) must be in relation.
Relation R1 = {(1, 2), (2, 1), (1, 1), (2, 2), (3, 3)}
Total possible pairs = {(1, 1) , (1, 2), (1, 3), (2, 1) , (2, 2), (2, 3), (3, 1) , (3, 2), (3, 3)}
The smallest relation is R1 = {(1, 2), (2, 1), (1, 1), (2, 2), (3, 3)}
Add (3, 2) also, as it is symmetric but, as (1, 2) and (2, 3) are there, (1, 3) is to be added as it is transitive.
Since we are adding (1, 3), (3, 1) also is to be added, as it is symmetric.
Relation R2 = {(1, 2), (2, 1), (1, 1), (2, 2), (3, 3), (2, 3), (3, 2), (1, 3), (3, 1)}
So, only 2 possible relations are there which are equivalence.
[ii] If sin-1 x = y, then
(A) 0 ≤ y ≤ 𝛑 (B) – 𝛑 / 2 ≤ y ≤ 𝛑 / 2
(C) 0 < y < 𝛑 (D) – 𝛑 / 2 < y < 𝛑 / 2
Solution: (B)
sin-1 x = y
y = sin-1 x
The range of principal value of sin is [- 𝛑 / 2, 𝛑 / 2].
So, – 𝛑 / 2 ≤ y ≤ 𝛑 / 2 is the correct answer.
[iii] If ![MPBSE class 12 2019 Questions and Solutions MPBSE Class 12 Maths 2019 QP Solutions Q1[iii]](https://cdn1.byjus.com/wp-content/uploads/2020/10/mpbse-class-12-maths-2019-qp-solutions-q1iii.png) and A + A’ = I, then the value of ɑ is
and A + A’ = I, then the value of ɑ is
(A) 𝛑 / 6 (B) 𝛑 / 3
(C) 𝛑 (D) 3𝛑 / 2
Solution: (B)
![MPBSE class 12 2019 Questions and Solutions MPBSE Class 12 Maths 2019 QP Solutions Q1[iii] answer](https://cdn1.byjus.com/wp-content/uploads/2020/10/mpbse-class-12-maths-2019-qp-solutions-q1iii-answer.png)
A + A’ = I
![MPBSE class 12 2019 Questions and Solutions MPBSE Class 12 Maths 2019 QP Solutions Q1[iii] answer](https://cdn1.byjus.com/wp-content/uploads/2020/10/mpbse-class-12-maths-2019-qp-solutions-q1iii-answer1.png)
![MPBSE class 12 2019 Questions and Solutions MPBSE Class 12 Maths 2019 QP Solutions Q1[iii] answer](https://cdn1.byjus.com/wp-content/uploads/2020/10/mpbse-class-12-maths-2019-qp-solutions-q1iii-answer2.png)
Since the matrices are equal, the corresponding elements can be equated.
2 cos ɑ = 1
cos ɑ = 1 / 2
cos ɑ = cos 60o
ɑ = 𝛑 / 3
[iv] Let A be a nonsingular square matrix of order 3 x 3, then adj |A| is equal to
(A) |A|2 (B) |A| (C) |A|3 (D) 3|A|
Solution: A
A (adj A) = |A| I
Taking determinants both sides
|A (adj A)| = ||A| I|
|A (adj A)| = |A| |adj A| (|𝐴𝐵|=|𝐴||𝐵|)
||A|I| = |A|3|I| = |A|3
|A (ad jA)| = ||A|I|
Putting values
|A| |adj (A)| = |A|3
|adj (A)| = |A|3 / |A|
|adj (A)| = |A|2
B is the correct answer.
[v] Function f (x) = |x| at x = 0 is
(A) Continuous but not differentiable
(B) Discontinuous and not differentiable
(C) Discontinuous and differentiable
(D) Continuous and differentiable
Solution: (A)
f (x) = |x|
![MPBSE class 12 2019 Questions and Solutions MPBSE Class 12 Maths 2019 QP Solutions Q1[v]](https://cdn1.byjus.com/wp-content/uploads/2020/10/mpbse-class-12-maths-2019-qp-solutions-q1v.png)
f is continuous at x = 0 if the left-hand limit is equal to the right-hand limit.
lim x→0- f (x) = lim x→0+ f (x) = f (0)
LHL = lim x→0- f (x)
= lim x→0- |x|
= lim x→0 (-x)
= – (0)
= 0
RHL = lim x→0+ f (x)
= lim x→0+ |x|
= lim x→0 (x)
= 0
LHL = RHL and f (0) = 0.
Hence lim x→0- f (x) = lim x→0+ f (x) = f (0).
f is continuous at x = 0.
Question 2: Fill in the blanks. 1 * 5 = 5M
[i] The direction cosine of the vector 3i – 2j + 6k are _____. [3 / 7, -2 / 7, 6 / 7] [ii] If y = x + ex, then d2y / dx2 = _____. [d2y / dx2 = ex]Solution:
y = x + ex
dy / dx = 1 + ex
d2y / dx2 = ex
[iii] Area bounded by the curve y = x2, x – axis and x = 1 and x = 2, is _____. [7 / 3]Solution:
∫12 x2 dx
= (x3 / 3)12
= 1 / 3 (23 – 13)
= 7 / 3
[iv] Direction ratio of two parallel lines will be in _____. [proportion] [v] Intercept of 2x + y – z = 5 on x-axis is _____. [5 / 2]Solution:
2x + y – z = 5
Since it cuts the x-axis, y and z = 0.
2x = 5
x = 5 / 2
Question 3: Write true/false in the following statements. 1 * 5 = 5M
(i) If E1 and E2 are exclusive events, then P (E1 ⋂ E2) is 0. [True]
(ii) If P (A) = 1 / 2, P (B) = 0, then P (A / B) is not defined. [True]
(iii) The objective function of an LPP is always linear. [True]
(iv) The feasible region of a linear programming problem is always a linear
Polygon. [True]
(v) The value of ∫0𝛑 cos3 x dx is 0. [True]
Question 4: Match the correct pairs. 1 * 5 = 5M

Solution:
(i) – (c)
(ii) – (a)
(iii) – (d)
(iv) – (f)
(v) – (g)
Question 5: Write the answers in one word/sentence each. 1 * 5 = 5M
(i) The maximum value of x1/x is
Solution:
y = x1/x
log y = (1 / x) log x
(1 / y) (dy / dx) = (1 – logx) / x2
dy / dx = 0
1 – logx = 0
log x = 1
x = e
The maximum value is e1/e.
(ii) Rate of change in the area of a circle having radius r when r = 5 cm.
Solution:
Area of circle = A = 𝛑r2
dA / dr = d (𝛑r2) / dr
= 2𝛑r
For r = 5,
dA / dr = 2𝛑 * 5 = 10𝛑
(iii) The slope of the normal to the curve y = 2x2 + 3 sin x at x = 0.
Solution:
y = 2x2 + 3 sin x
dy / dx = 4x + 3 cos x
Slope of tangent * Slope of normal = -1
(4x + 3 cos x) * Slope of normal = -1
Slope of normal = -1 / (4x + 3 cos x)
At x = 0,
Slope of normal = -1 / (4 * 0 + 3 cos 0)
= -1 / 3
(iv) The minimum value of 3 sin θ + 4 cos θ is
Solution:
Let f (θ) = 3 sin θ + 4 cos θ
f ‘ (θ) = 3 cos θ – 4 sin θ —- (1)
f ‘’ (θ) = – 3 sin θ – 4 cos θ —- (2)
Now for maximum of minimum value of f (θ), f ′(θ) = 0.
3 cos θ – 4 sin θ = 0
sin θ = ± 3 / 5; cos θ = ± 4 / 5
From (2), sin θ = – 3 / 5; cos θ = – 4 / 5
f ‘’ (θ) > 0
The minimum value of f (θ) = – (32 + 42) / 5 = -5.
(v) Derive the equation of tangent line at (1, 1) on curve y = x3.
Solution:
dy / dx = 3x2
At (1, 1), dy / dx = 3
y – 1 = 3 (x – 1)
y – 1 = 3x – 3
y = 3x – 2
SECTION – B
Question 6: [i] If  then find the value of A . B.
then find the value of A . B.
OR
[ii] If  then find the value of A – B.
then find the value of A – B.
Solution:
[i]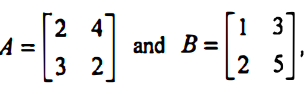

OR
[ii]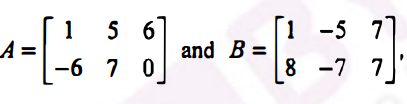

Question 7: [i] Check the continuity of the function f given by f (x) = 2x + 3 at x = 1.
OR
[ii] Prove that the modulus function f (x) = |x| is not differentiable at x = 0.
Solution:
[i] The function is continuous at x = 1 if lim x→1 f (x) = f (1).LHS = lim x→1 f (x)
= lim x→1 (2x + 3)
= 2 * 1 + 3
= 5
RHS = f (1)
= 2 * 1 + 3
= 5
LHS = RHS
The function is continuous.
OR
[ii] |x| = f (x) = x x ≥ 0– x x < 0
f (x) is not differentiable at x = 0.
f ‘ (x) = x / |x|
Question 8: [i] Find the following integrals ∫(x2/3 + 1) dx.
OR
[ii] Find the following integrals ∫[(1 – sinx) / cos2 x] dx.
Solution:
[i] ∫(x2/3 + 1) dx= ∫(x2/3 + x0) dx
= ∫x2/3 dx + x0 dx
= ∫x(2/3) + 1 / [(2 / 3) + 1] + ∫x0 + 1 / [0 + 1] + c
= x(5/3) / [(5 / 3)] + x + c
= (3x5/3 / 5) + x + c
OR
[ii]

Question 9: [i] Find the unit vector in the direction of vector a = 2i + 3j + k.
OR
[ii] Find the projection of the vector a = 2i + 3j + 2k on the vector b = i + 2j + k.
Solution:
[i] a = 2i + 3j + k = 2i + 3j + 1k|a| = √22 + 32 + 12
= √4 + 9 + 1
= √14
Unit vector = a / |a|
= 2i + 3j + 1k / √14
= (2 / √14) i + (3 / √14) j + (1 / √14) k
OR
[ii] a = 2i + 3j + 2kb = i + 2j + k
(a . b) = (2 * 1) + (3 * 2) + (2 * 1)
= 2 + 6 + 2
= 10
|b| = √12 + 22 + 1
= √1 + 4 + 1
= √6
Projection of vector a on b = (a . b) / |b|
= (1 / √6) (10)
= 10 / √6
= (10 / √6) (√6 / √6)
= (10 / 6) (√6)
= (5 / 3) (√6)
Question 10: [i] Find the equation of the plane whose intercepts on the coordinate axes are -4, 2, 3.
OR
[ii] Find the angle between the line (x + 1) / 2 = (y / 3) = (z – 3) / 6 and the plane 3x + y + z = 7.
Solution:
[i] The intercepts of the plane equation are – 4, 2, 3.(x / – 4) + (y / 2) + (z / 3)
OR
[ii] (x + 1) / 2 = (y / 3) = (z – 3) / 6The plane is 3x + y + z = 7.
sin ɸ = (2 * 3 + 3 * 1 + 6 * 1) / (√4 + 9 + 36) (9 + 1 + 1)
= (6 + 3 + 6) / 7 * √11
= 15 / 7√11
ɸ = sin-1 (15 / 7√11)
Question 11: [i] The radius of an air bubble is increasing at the rate 1 / 2 cm per second. At what rate is the volume of the bubble increasing when the radius is 1 cm.
OR
[ii] Find the slope of the normal to the curve x = 1 – a sin θ, y = bcos2 θ at
θ = 𝛑 / 2.
Solution:
[i] Consider r is the radius of the bubble.It is given that dr / dt = (1 / 2) cm / s — (1)
The bubble is in the shape of a sphere.
So, the volume of the bubble = volume of the sphere = (4 / 3) 𝛑r3
dv / dt at r = 1 cm
dv / dt = d ((4 / 3) 𝛑r3) / dt
= [(4 / 3) 𝛑] 3r2 (dr / dt)
= 4𝛑r2 (1 / 2)
= 2𝛑r2
When radius is 1 cm, dv / dt = 2𝛑 (1)2
= 2𝛑 cm3 / sec
OR
[ii] x = 1 – a sin θ, y = bcos2 θdx / dθ = 0 − a cos θ
dy / dθ = − 2b cos θ sin θ
dy / dx = (dy / dθ) / (dx / dθ)
= (− 2b cos θ sin θ) / (− a cos θ)
= (2b / a) sin θ
The slope of the tangent at θ = 𝛑 / 2 is given by,
(dy / dx)θ = 𝛑 / 2 = [(2b / a) sin θ]θ = 𝛑 / 2
= (2b / a) sin (𝛑 / 2)
= 2b / a
The slope of the normal at θ = 𝛑 / 2 is given by,
1 / (slope of the tangent at θ = 𝛑 / 4) = – 1 / (2b / a)
= – a / 2b
Question 12: [i] For what value of x is y = x (5 – x) maximum or minimum?
OR
[ii] Use differentials to find the value of √49.5.
Solution:
[i] y = x (5 – x)y = 5x – x2
dy / dx = 5 – 2x
dy / dx = 0
5 – 2x = 0
x = 5 / 2
d2y / dx2 = – 2 (negative)
x = 5 / 2 is maximum and no minimum.
OR
[ii] Consider x = 49 and δx = 0.5.y = x1/2
dy / dx = 1 / 2√x
= 1 / 2 * (49)
= 1 / (2 * 7)
= 1 / 14
δy = (dy / dx) (δx)
= (1 / 14) (0.5)
= 1 / 28
√49.5 = y + δy
= 7 + (1 / 28)
= 7.036
Question 13: [i] If a + b + c = 0, then prove that a x b = b x c = c x a.
OR
[ii] Find the area of parallelogram whose adjacent sides are given by the vectors a = 3i + j + 4k and b = i – j + k.
Solution:
[i] a + b + c = 0a x (a + b + c) = a x 0
a x a + a x b + a x c = a x 0
0 + a x b + a x c = a x 0
a x b + a x c = 0
a x b = – a x c
a x b = c x a
Similarly
a + b + c = 0
b x (a + b + c) = b x 0
b x a + b x b + b x c = b x 0
b x a + b x b + b x c = b x 0
b x a + b x c = 0
b x c = – b x a
b x c = a x b
a x b = b x c = c x a
OR
[ii] a = 3i + j + 4kb = i – j + k
Area of the parallelogram = |a x b|
a x b =

= i (1 × 1 – (−1) × 4) − j (3 × 1 – 1 × 4) + k (3 × −1 − 1 × 1)
= i (1 − (– 4)) − j (3 − 4) + k (−3 −1)
= i (1 + 4) − j (−1) + k (− 4)
= 5i + j − 4k
Magnitude of a x b = √(52 + 12 + (−4)2)
|a x b| = √(25 + 1 + 16)
= √42
Area of parallelogram = |a x b| = √42
Question 14: [i] Find the minimum distance between the line l1 and l2 given by
r = i + 2j – 4k + ƛ (2i + 3j + 6k)
r = 3i + 3j – 5k + µ (2i + 3j + 6k)
OR
[ii] Find the distance of the plane 2x – 3y + 4z – 6 = 0 from the origin.
Solution:
[i] r = i + 2j – 4k + ƛ (2i + 3j + 6k)r = 3i + 3j – 5k + µ (2i + 3j + 6k)
The above two lines passes through the points having position vectors,
a1 = i + 2j – 4k
a2 = 3i + 3j – 5k and are parallel to the vector b = 2i + 3j + 6k
a2 – a1 = 2i + j – k
(a2 – a1) b = (2i + j – k) (2i + 3j + 6k)
=

= 9i – 14j + 4k
|(a2 – a1) b| = √92 + (- 14)2 + 42
= √81 + 16 + 16
= √293
|b| = √22 + 32 + 62
= √4 + 9 + 36
= 7
Shortest distance = |(a2 – a1) b| / |b|
= √293 / 7
OR
[ii] The equation of the plane is 2x – 3y + 4z – 6 = 0.2x – 3y + 4z = 6 — (1)
The direction ratios are given by a = 2, b = – 3 and c = 4.
√a2 + b2 + c2 = √22 + (- 3)2 + 42
= √4 + 9 + 16
= √29
The direction cosines are l = 2 / √29, m = – 3 / √29, n = 4 / √29.
The equation of the plane is lx + my + nz = d.
(2 / √29) x + (- 3 / √29) y + (4 / √29) z = d
2x – 3y + 4z = d √29
On comparing with equation (1),
6 = d √29
d = 6 / √29
Question 15: [i] Show that relation “is equal to” in sets is an equivalence relation.
OR
[ii] If f (x) = x2 and g (x) = x + 3. x ∈ R , then find the value of (g o f) x , (f o g) x , (f o g)2.
Solution:
[i] The relation “is equal to”, denoted “=”, is an equivalence relation on the set of real numbers since for any x, y, z ∈ R:a. Reflexivity: x = x,
b. Symmetry: if x = y then y = x,
c. Transitivity: if x = y and y = z then x = z.
All of these are true.
OR
[ii] f (x) = x2 and g (x) = x + 3(g o f) x = g f (x)
= f (x) + 3
= x2 + 3
(f o g) x = f (g (x))
= (x + 3)2
= x2 + 9 + 6x
(f o g)2 = (2 + 3)2
= 52
= 25
Question 16: [i] Show that sin-1 (3 / 5) – sin-1 (8 / 17) = cos-1 (84 / 85).
OR
[ii] Prove that cos-1 x = 2 cos-1 √(1 + x) / 2.
Solution:
[i] sin-1(3 / 5) = x and sin-1(8 / 17) = ysinx = 3 / 5 ; siny = 8 / 17
cosx = √(1 – sin2x)
= √(1 – (3 / 5)2)
= √(1 – 9 / 25)
= 4/5
cosy = √(1 – sin2y)
= √(1 – (8 / 17)2)
= √(1 – 64 / 289)
= 15 / 17
cos (x – y) = cos x cos y + sin x sin y
= 4 / 5 x 15 / 17 + 3 / 5 x 8 / 17 = 60 / 85 + 24 / 85 = 84 / 85
⇒ x – y = cos-1 (84 / 85)
⇒ sin-1 (3 / 5) – sin-1 (8 / 17) = cos-1 (84 / 85)
OR
[ii] cos-1 x = 2 cos-1 √(1 + x) / 2Put x = cos θ
cos-1 cos θ = 2 cos-1 √(1 + cos θ) / 2
θ = 2 cos-1 √[1 + 2 cos2 θ / 2] / 2
= 2 cos-1 cos (θ / 2)
= θ
θ = θ
LHS = RHS
Question 17: [i] Prove that  .
.
OR
[ii] Find the area of the triangle whose vertices are (3, 8), (- 4, 2) and (5, 1).
Solution:
[i] Applying R1 → R1 – R2 – R3

= 0 + 2c (b (a + b) – cb) – 2b (cb – c(c + a))
= 2c (ab + b2 – cb) – 2b (cb – c2 – ca)
= 2abc + 2cb2 – 2bc2 – 2b2c + 2bc2 + 2abc
= 2abc + 2abc + 2cb2 – 2cb2 – 2bc2 + 2bc2
= 4abc + 0 + 0
= 4abc
OR
[ii] Area of the triangle = (1 / 2)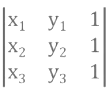
Δ = (1 / 2)

= (1 / 2) (3 (2 – 1) – 8 (- 4 – 5) + 1 (- 4 – 10))
= (1 / 2) (3 + 72 – 14)
= 61 / 2
Question 18: [i] Find the equation of the plane the coordinate point (1, – 1, 2) and is perpendicular to each of the planes 2x + 3y – 2z = 5 and x + 2y – 3z = 8.
OR
[ii] Show that the angle between any two diagonals of a cube is cos-1 (1 / 3).
Solution:
[i] The equation of any plane passing through the point is (1, -1, 2) isa (x – 1) + b (y + 1) + c (z – 2) = 0 —- (1)
It is given that (1) is perpendicular to the plane 2x + 3y – 2z = 5.
2a + 3b – 2c = 0 —- (2)
It is given that (1) is perpendicular to the plane x + 2y – 3z = 8.
a + 2b – 3c = 0 —- (3)
On solving (1), (2), (3),

– 5 (x – 1) + 4 (y + 1) + 1 (z – 2) = 0
5x – 4y – z = 7
OR
[ii] Consider a to be the edge of the cube with vertex at the origin.There exist our diagonals for a cube.
The direction ratios of the diagonals are given by
(a – 0), (a – 0), (a – 0) = a, a, a and (0 – a), (a – 0), (a – 0) = a, a, a
Let θ be the angle between the diagonals.
cos θ = a (-a) + a (a) + a (a) / [√a2 + a2 + a2 √- a2 + a2 + a2]
= a2 / 3a2
= 1 / 3
cos θ = 1 / 3
θ = cos-1 (1 / 3)
Question 19: [i] Draw the graph of the inequality 3x + 2y ≤ 6.
OR
[ii] Find the minimum value of P = 2x + 4y, subject to constraints:
4x + 3y ≤ 12
x + 2y ≥ 4
x, y ≥ 0
Solution:
[i]

OR
[ii]

|
Points |
P = 2x + 4y |
|
(0, 0) |
0 |
|
(3, 0) |
6 |
|
(12 / 5), (4 / 5) |
8 |
|
(0, 2) |
8 |
The value is minimum at the origin.
Question 20: [i] If P (A) = ½, P (B) = ¼ and P (A ⋂ B) = ¼, then find the following:
(i) P (A / B)
(ii) P (B / A)
OR
[ii] In four throws of two dice what is the probability of getting the same figure on both dice?
Solution:
[i] P (A) = ½P (B) = ¼
P (A ⋂ B) = ¼
(i) P (A / B) = P (A ⋂ B) / P (B)
= (1 / 4) / (1 / 4)
= 1
(ii) P (B / A) = P (A ⋂ B) / P (A)
= (1 / 4) / (1 / 2)
= 1 / 2
OR
[ii] n = 4p = 6 / 36 = 1 / 6
q =1 – (1 / 6) = 5 / 6
P (success) = 1 – P (no doublet)
= 1 – P (X = 0)
= 1 – 4C0 (5 / 6)4-0 (1 / 6)0
= 1 – (5 / 6)4
= 1 – (625 / 1296)
= 671 / 1296
Question 21: [i] A family has two children. What is the probability that both the children are boys given that at least one of them is a boy?
OR
[ii] Find the probability distribution of numbers of doublets in three throws of a pair of dice.
Solution:
[i] Sample space = S = {BB, BG, GB, GG} where B = Boy, G = GirlA: at least one of the children is boy: {BB, BG, GB}
B: both are boys: {BB}
P (B / A) = P (A ⋂ B) / P (A)
= (1 / 4) / (3 / 4)
= 1 / 3
OR
[ii] The possible number of doublets possible on the throwing of 2 dice is(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)
P (getting a doublet) = 6 / 36 = 1 / 6
P (not getting a doublet) = 1 – 1 / 6 = 5 / 6
When two dies are thrown thrice, 0 doublet or 1 doublet or 2 doublets or 3 doublets can be obtained.
X can take values 0, 1, 2, 3.
P (X = 0)
P (X = 0) = P (0 doublet on three throws)
= 5 / 6 × 5 / 6 × 5 / 6
= 125 / 216
P (X = 1)
P (X = 1) = P (one doublet on three throws)
= 1 / 6 × 5 / 6 × 5 / 6 + 5 / 6 × 1 / 6 × 5 / 6 + 5 / 6 × 5 / 6 × 1 / 6
= 3 × 5 / 6 × 5 / 6 × 1 / 6
= 75 / 216
P(X = 2)
P(X = 2) = P(two doublet on three throws)
= 1 / 6 × 1 / 6 × 5 / 6 + 1 / 6 × 5 / 6 × 1 / 6 + 5 / 6 × 1 / 6 × 1 / 6
= 3 × 1 / 6 × 1 / 6 × 5 / 6
= 15 / 216
P(X = 3)
P(X = 3) = P(three doublets on three throws)
= 1 / 6 × 1 / 6 × 1 / 6
= 1 / 216
The probability distribution is
|
X |
0 |
1 |
2 |
3 |
|
P(X) |
125 / 216 |
75 / 216 |
15 / 216 |
1 / 216 |
Question 22: [i] If  , then prove that A’ . A = I.
, then prove that A’ . A = I.
OR
[ii] If  then verify that
then verify that
(a) (A’)’ = A
(b) (A + B)’ = A’ + B’
Solution:
[i]

OR
[ii] (a)
![MPBSE class 12 2019 Questions and Solutions MPBSE Class 12 Maths 2019 QP Solutions Q22ii [a] answer](https://cdn1.byjus.com/wp-content/uploads/2020/10/mpbse-class-12-maths-2019-qp-solutions-q22ii-a-answer.png)
(b)
![MPBSE class 12 2019 Questions and Solutions MPBSE Class 12 Maths 2019 QP Solutions Q22ii [b] answer](https://cdn1.byjus.com/wp-content/uploads/2020/10/mpbse-class-12-maths-2019-qp-solutions-q22ii-b-answer.png)
Question 23: [i] Discuss the continuity of the following function 
OR
[ii] Prove that the function

is not differentiable at x = 1.
Solution:
[i] Continuity is defined byf (x) is continuous at x = a ⇔ lim x→a f (x) = f (a)
To show that lim x→0 (x) sin (1 / x) = f (0)
Let z = 1 / x, then as x → 0, z → ∞
lim x→0 (x) sin (1 / x) = lim z → ∞ (1 / z) sin z
= lim z → ∞ sin z / z
= 0
OR
[ii]

y = 1 – x
y = x2 – 1
x2 = y + 1
From the graph, the function is not differentiable at x = 1.
Question 24: [i] Evaluate ∫(xex) / (1 + x2) dx.
OR
[ii] Evaluate ∫01 (tan-1 x) / (1 + x2) dx.
Solution:
[i] Let I = ∫xex (1 + x)2 dxI = ∫(x + 1 – 1)ex / (1 + x)2 dx
I = ∫ex (1 + x) dx – ∫ex (1 + x)2 dx
Applying integration by parts in first integral,
= ex / (1 + x) – ∫- (1 / (1 + x)2) ex dx – ∫ex / (1 + x)2 dx + C
= ex / (1 + x) + ∫ (1 / (1 + x)2) ex dx – ∫ex / (1 + x)2 dx + C
I = ex / 1 + x) + C
OR
[ii] Let tan−1 x = tdx / 1 + x2 = dt
When x = 0, t = tan−1 0 = 0
When x = 1, t = tan−1 1 = π / 4
I =∫0π/4 t dt
= [t2 / 2]
= (1 / 2) [t2]
= (1 / 2) (π / 4)2 − 0
= π2 / 32
Question 25: [i] Find the area enclosed by circle x2 + y2 = a2.
OR
[ii] Find the area of region bounded by the curves y1 = sin x and y2 = cosx
between x = 0 and x = π / 4.
Solution:
[i] The equation of circle is: x2 + y2 = a2y2 = a2 – x2
y = √a2 – x2
Area of circle = 4 × Area of first quadrant
= 4∫a0 y dx
= 4∫a0√(a2 – x2)dx
= 4 [x / 2 (√(a2 – x2)) + (a2 / 2) sin-1 x / a]a0
= 4 [0 + (a2 / 2) sin-1 a / a – ( 0 + (a2 / 2) sin-1 0 / a) ]
= 4 [(a2 / 2) sin-1 1 – 0 ]
= 2a2 (π / 2)
= πa2 square units
OR
[ii] y1 = sin x and y2 = cosxArea = ∫0π/4 (cosx – sinx) dx
= [sinx + cosx]0π/4
= sin (π / 4) + cos (π / 4) – [sin 0 + cos 0]
= (1 / √2) + (1 / √2) – [0 + 1]
= (2 / √2) – 1
= √2 – 1 square units
Question 26: [i] Verify that the function y = a cosx + b sin x. where a, b ∈ R is a solution of the differential equation d2y / dx2 + y = 0.
OR
[ii] Solve the differential equation dy / dx = x · log x.
Solution:
[i] y = a cosx + b sinxdy / dx = – a sinx + b cosx
d2y / dx2 = – a cos x – b sinx
LHS = d2y / dx2 +y
= – a cosx – b sinx + a cosx + b sinx
= 0
= RHS
OR
[ii] y = x2 log x − x2 / 2+ey = [x3 / 2] log x − x2 + c
y = (1 / 2) x2 + (1 / 2) x2 log x + c
y = (x2 / 2) logx − x2 / 4 + c































Comments