MSBSHSE Solutions For SSC (Class 10) Maths Part 1 Chapter 5 Probability

MSBSHSE Solutions For SSC (Class 10) Maths Part 1 Chapter 5 Probability is considered to be very useful when you are preparing for the Class 10 Maths exams. Here, we bring to you detailed answers to the exercises of Chapter 5 Probability. Subject matter experts who created the solutions have collected these questions for you to revise from chapter 5 of SSC 10th Maths Maharashtra Board Textbook. These questions have been devised as per the Maharashtra Board syllabus and the guidelines. Students can refer to this study material to boost their confidence, and attempt the exam smartly. The concepts are explained with steps, shortcuts to remember formulae, tips, and tricks to solve the numerical problems wisely and quickly. This chapter of Maharashtra Solutions for Class 10 mainly focuses on the concept of probability, its experimental approach in detail. Let us have a look at some of the important concepts that are discussed in this chapter.

• Random Experiment
• Outcome
• Equally Likely Outcomes
• Sample Space
• Event
• Chances of occurrence of an event

Download the PDF of Maharashtra Solutions For SSC Maths Part 1 Chapter 5 Probability

Access answers to Maths MSBSHSE Solutions For SSC Part 1 Chapter 5 – Probability

Practice set 5.1 Page no: 116

1. How many possibilities are there in each of the following?
(1) Vanita knows the following sites in Maharashtra. She is planning to visit one of them in her summer vacation.
Ajintha, Mahabaleshwar, Lonar Sarovar, Tadoba wild life sanctuary, Amboli, Raigad, Matheran, Anandavan.

Solution:

There are 8 possibilities.

(2) Any day of a week is to be selected randomly.

Solution:

In a week comprising of 7 days, there are 7 ways to select any day.

(3) Select one card from the pack of 52 cards.

Solution:

There are 52 possibilities.

(4) One number from 10 to 20 is written on each card. Select one card randomly.

Solution:

There are 11 total ways of selecting a card randomly.

Practice set 5.2 Page no: 117

1. For each of the following experiments write sample space ‘S’ and number of sample points n(S).
(1) One coin and one die are thrown simultaneously.

Solution:

(1) Given one coin and one die are thrown simultaneously.

Sample Space, S = {1H, 1T, 2H, 2T, 3H, 3T, 4H, 4T, 5H, 5T, 6H, 6T}

Number of events in Sample Space S, n(S) = 12

(2) Two-digit numbers are formed using digits 2, 3 and 5 without repeating a digit.

Solution:

Given two-digit numbers are formed using digits 2, 3 and 5 without repeating a digit

Sample Space, S = {23, 25, 32, 35, 52, 53}

Number of events in Sample Space S, n(S) = 6

2. The arrow is rotated and it stops randomly on the disc. Find out on which colour it may stop.

Solution:

Given the arrow is rotated and it stops randomly on the disc

Sample Space, S = {Red, Purple, Orange, Yellow, Blue, Green}

Number of events in Sample Space S, n(S) = 6

Practice set 5.3 Page no: 121

1. Write sample space ‘S’ and number of sample point n(S) for each of the following experiments. Also write events A, B, C in the set form and write n(A), n(B), n(C).
(1) One die is rolled,
Event A: Even number on the upper face.
Event B: Odd number on the upper face.
Event C: Prime number on the upper face.

Solution:

Given Event A: Even number on the upper face.

Event B: Odd number on the upper face.

Event C: Prime number on the upper face.

Sample space, S = {1, 2, 3, 4, 5, 6}

Number of sample points, n(S) = 6

A = {2, 4, 6}, n(A) = 3

B = {1, 3, 5}, n(B) = 3

C = {2, 3, 5}, n(C) = 3

(2) Two dice are rolled simultaneously,
Event A: The sum of the digits on upper faces is a multiple of 6.
Event B: The sum of the digits on the upper faces is minimum 10.
Event C: The same digit on both the upper faces.

Solution:

Given Two dice are rolled simultaneously,

Event A: The sum of the digits on upper faces is a multiple of 6.

Event B: The sum of the digits on the upper faces is minimum 10.

Event C: The same digit on both the upper faces.

Sample space, S = {(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1), (2,2),(2,3),(2,4),(2,5),(2,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),(5,1),(5,2),(5,3),(5,4),(5,5),(5, 6),(6, 1),(6,2),(6,3),(6,4),(6,5),(6, 6)}

Number of sample points, n(S) = 36

A = {(1, 5) (2, 4) (3, 3) (4, 2) (5, 1) (6, 6)}, n(A) = 6

B = {(4, 6) (5, 5) (5, 6) (6, 4) (6, 5) (6, 6)}, n(B) = 6

C = {(1, 1) (2, 2) (3, 3) (4, 4) (5, 5) (6, 6)}, n(C) = 6

(3) Three coins are tossed simultaneously.
Condition for event A: To get at least two heads.
Condition for event B: To get no head.
Condition for event C: To get head on the second coin.

Solution:

Given Three coins are tossed simultaneously.

Condition for event A: To get at least two heads.

Condition for event B: To get no head.

Condition for event C: To get head on the second coin

Sample Space, S = {HHH, HHT, HTT, HTH, THT, TTH, THH, TTT}

Number of sample points, n(S) = 8

To get at least two heads, A = {HHH, HHT, HTH, THH}

n(A) = 4

To get no head, B = {TTT}

n(B) = 1

To get head on the second coin, C = {HHH, HHT, THH}

n(C) = 3

Practice set 5.4 Page no: 125

1. If two coins are tossed, find the probability of the following events.
(1) Getting at least one head.

Solution:

Given two coins are tossed

Sample Space, S = (HH, HT, TH, TT)

Probability of getting at least one head, p(A) =

p(A) = ¾

(2) Getting no head.

Solution:

Given two coins are tossed

Sample Space, S = (HH, HT, TH, TT)

Probability of getting no head, p(B) =

p(B) = ¼

2. If two dice are rolled simultaneously, find the probability of the following events.
(1) The sum of the digits on the upper faces is at least 10.

Solution:

Given the sum of the digits on the upper faces is at least 10.

Probability of getting the sum of the digits on the upper faces is at least 10, p (A) =

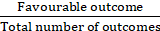
We know the favorable cases are (Where the Sum of digits on the upper faces is at least 10) = (4,6), (5,5), (5,6), (6,4), (6,5), (6,6) = 6 cases

Total Number of Outcomes = 36

p (A) = 6/36 = 1/6

(2) The sum of the digits on the upper faces is 33.

Solution:

Given the sum of the digits on the upper faces is 33.

Probability of getting the sum of the digits on the upper faces is 33, p (B) =

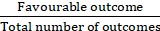
Favourable outcomes (Getting the sum of Digits on the upper Faces is 33) = 0 as the maximum sum could be 12

p(B) = 0

(3) The digit on the first die is greater than the digit on second die.

Solution:

Given the digit on the first die is greater than the digit on second die.

Probability of getting the digit on the first die is greater than the digit on second die, p(C) =

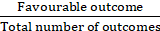
Favorable Outcomes are as follow = (2,1), (3,1), (3,2), (4,1), (4,2), (4,3), (5,1), (5,2), (5,3), (5,4), (6,1), (6,2), (6,3),(6,4), (6,5) = 15 cases

p(C) = 15/36 = 5/12

Problem set 5 Page no: 126

1. Choose the correct alternative answer for each of the following question.

(1) Which number cannot represent a probability?
A. 2/3
B. 1.5
C. 15%
D. 0.7

Solution:

B. 1.5

Explanation:

As probability of any event lies between 0 and 1, the answer is option B = 1.5, which is greater than 1.

(2) A die is rolled. What is the probability that the number appearing on upper face is less than 3?
A. 1/6
B. 1/3
C. 1/2
D. 0

Solution:

B. 1/3

Explanation:

Favorable outcomes = (1, 2) = 2

Total number of outcomes=6

Probability that the number appearing on upper face is less than 3 = 2/6 = 1/3

(3) What is the probability of the event that a number chosen from 1 to 100 is a prime number?
A. 1/5
B. 6/25
C. 1/4
D. 13/50

Solution:

B. 6/25

Explanation:

Favorable outcomes=24

Total number of outcomes=100

Probability that the number a number chosen from 1 to 100 is a prime number = 24/100 = 6/25

(4) There are 40 cards in a bag. Each bears a number from 1 to 40. One card is drawn at random. What is the probability that the card bears a number which is a multiple of 5?
A. 1/5
B. 3/5
C. 4/5
D. 1/3

Solution:

A. 1/5

Explanation:

Favorable outcomes=8

Total number of outcomes=40

Probability that the card bears a number which is a multiple of 5 = 8/40 = 1/5

(5) If n(A) = 2, P(A) = 1/5, then n(S) =?
A. 10
B. 5/2
C. 2/5
D. 1/3

Solution:

A. 10

Explanation:

Probability, P(A) = n (A)/ n (s)

⇒ 1/5 = 2/ n(s)

n(S)=10

2. Basketball players John, Vasim, Akash were practising the ball drop in the basket. The probabilities of success for John, Vasim and Akash are 4/5 0.83 and 58% respectively. Who had the greatest probability of success?

Solution:

Given the probabilities of success for John, Vasim and Akash are 4/5 0.83 and 58% respectively.

Probability of success for John = 4/5 = 0.8

Probability of success for Vasim = 0.83

Probability of success for Akash = 0.58

Therefore, probability of success is highest for = Vasim

3. In a hockey team there are 6 defenders, 4 offenders and 1 goalee. Out of these, one player is to be selected randomly as a captain. Find the probability of the selection that –

(1) The goalee will be selected.

Solution:

Probability of the selection that the goalee will be selected, p(G) =

Therefore, p(G)= 1/11

(2) A defender will be selected.

Solution:

Probability of the selection that the goalee will be selected, p(D) =

p(D) = 6/11

4. Joseph kept 26 cards in a cap, bearing one English alphabet on each card. One card is drawn at random. What is the probability that the card drawn is a vowel card?

Solution:

Given one card is drawn at random.

Probability of the selection that the card drawn is a vowel card, p(V) =

p(V) = 5/26

5. A balloon vendor has 2 red, 3 blue and 4 green balloons. He wants to choose one of them at random to give it to Pranali. What is the probability of the event that Pranali gets,
(1) a red balloon
(2) a blue balloon
(3) a green balloon.

Solution:

(1) Probability that Pranali gets a red balloon, p(R) =

p(V) = 4/9

(2) Probability that Pranali gets a blue balloon, p(B) =

p(B) = 1/3

(3) Probability that Pranali gets a green balloon, p(G) =

p(G) = 4/9

6. A box contains 5 red, 8 blue and 3 green pens. Rutuja wants to pick a pen at random. What is the probability that the pen is blue?

Solution:

Probability that Rutuja picks blue pen, p(B) =

p(B) = 8/16 = ½

Probability is a part of math that deals with the occurrence of an event. To make it simpler, take the case of tossing a coin, when a coin is tossed in the air, the possible outcomes are Head and Tail. So, probability of occurrence of head is ½. The concept related to Probability is explained in BYJU’S to help the students be thorough with the topics.