MSBSHSE Solutions For SSC (Class 10) Maths Part 2 Chapter 1 – Similarity consists of accurate solutions, which helps the students to quickly complete their homework and prepare well for the exams. BYJU’S provides clear and step by step solutions prepared by our subject matter experts. Students can easily master the concepts of Similarity. We come across Basic proportionality theorem, Property of parallel lines and transversals, different tests for similarity of triangles in this chapter. These solutions are really helpful to get a better understanding of theorems of Similarity. Maharashtra State Board Solutions Class 10 can be downloaded in PDF format. These solutions help to develop confidence among students who are preparing for exams.
Download the PDF of Maharashtra Solutions For SSC Maths Part 2 Chapter 1 Similarity
Access answers to Maths MSBSHSE Solutions For SSC Part 2 Chapter 1 – Similarity
Practice set 1.1 Page 5
1. Base of a triangle is 9 and height is 5. Base of another triangle is 10 and height is 6. Find the ratio of areas of these triangles.
Solution:
Let base of the first triangle is b1 and height is h1. Let base of second triangle is b2 and height is h2.
Ratio of areas of two triangles is equal to the ratio of the products of their bases and corresponding heights.
Here b1 = 9
h1 = 5
b2 = 10
h1 = 6
Then ratio of their areas = b1×h1/b2×h2
= 9×5/10×6
= 3/4
Hence the ratio of the areas of these triangles is 3:4
2. In figure 1.13 BC⊥ AB, AD⊥ AB, BC = 4, AD = 8, then find A(ABC) /A( ADB) .
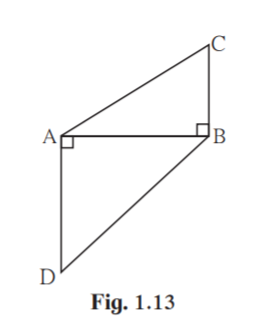
Solution:
Here ABC and ADB have the same base AB.
Areas of triangles with equal bases are proportional to their corresponding heights.
Since bases are equal, areas are proportional to heights.
Given BC = 4 and AD = 8
So, A(ABC) /A( ADB) = BC/AD
= 4/8
= 1/2
Hence ratio of areas of ABC and ADB is 1:2.
3. In adjoining figure 1.14 seg PS ⊥ seg RQ, seg QT ⊥ seg PR. If RQ = 6, PS = 6 and PR = 12, then find QT.
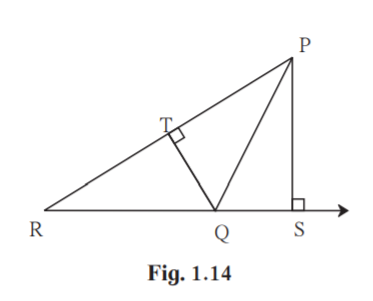
Solution:
Given PS ⊥ RQ and QT ⊥ PR.
RQ = 6
PS = 6
PR = 12
Area of PQR with base PR and height QT = (1/2)×PR×QT
Area of PQR with base QR and height PS = (1/2)×QR×PS
A(PQR)/ A(PQR) = (1/2)×PR×QT /(1/2)×QR×PS
1 = PR×QT/ QR×PS
1 = 12×QT/6×6
6×6 = QT×12
QT = 36/12
QT = 3
Hence measure of side QT is 3 units.
4. In adjoining figure, AP ⊥ BC, AD || BC, then find A( ABC):A( BCD).
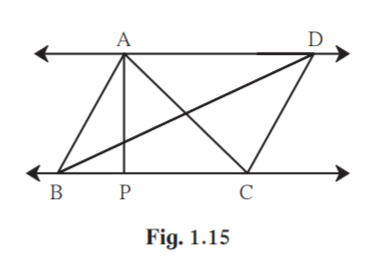
Solution:
Given , AP ⊥ BC, and AD || BC. ABC and BCD has same base BC.
Areas of triangles with equal bases are proportional to their corresponding heights.
Since AP is the perpendicular distance between parallel lines AD and BC, height of ABC and height of BCD are same.
A( ABC) /A( BCD) = AP/AP = 1
Hence A( ABC): A( BCD) = 1:1
5. In adjoining figure PQ ⊥ BC, AD ⊥ BC then find following ratios.
(i) A( PQB) /A( PBC)
(ii) A(PBC) / A( ABC)
(iii) A( ABC) /A( ADC)
(iv) A( ADC) /A( PQC)
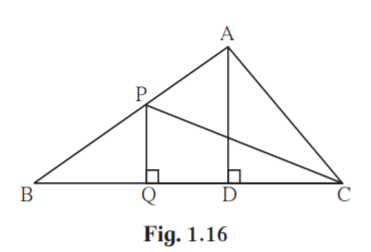
Solution:
(i) PQB and PBC have same height PQ.
Ratio of areas of triangles with equal heights are proportional to their corresponding bases.
A(PQB )/A(PBC) = BQ/BC
(ii) PBC and ABC have same base BC.
Ratio of areas of triangles with equal bases are proportional to their corresponding heights.
A(PBC) / A( ABC) = PQ/AD
(iii) ABC) and ADC have equal heights AD.
Ratio of areas of triangles with equal heights are proportional to their corresponding bases.
A( ABC) /A( ADC) = BC/DC
(iv) Ratio of areas of two triangles is equal to the ratio of the products of their bases and corresponding heights.
A( ADC) /A( PQC) = DC×AD/QC×PQ
Practice set 1.2 Page 13
1. Given below are some triangles and lengths of line segments. Identify in which figures, ray PM is the bisector of QPR.

Solution:
(i) In PQR
QM/RM = 35/15 = 7/3 …..(i)
PQ/PR = 7/3……………….(ii)
From (i) and (ii) QM/RM = PQ/PR
By Converse of angle bisector theorem , Ray PM is the bisector of QPR.
(ii) InPQR
PR/PQ = 7/10……..(i)
RM/QM = 6/8……..(ii)
From (i) and (ii) PR/PQ ≠ RM/QM
Ray PM is not the bisector of QPR
(iii) In PQR
PR/PQ = 10/9………(i)
RM/QM = 4/3.6 = 40/36 = 10/9 ……..(ii)
From (i) and (ii) PR/PQ = RM/QM
By Converse of angle bisector theorem , Ray PM is the bisector of QPR.
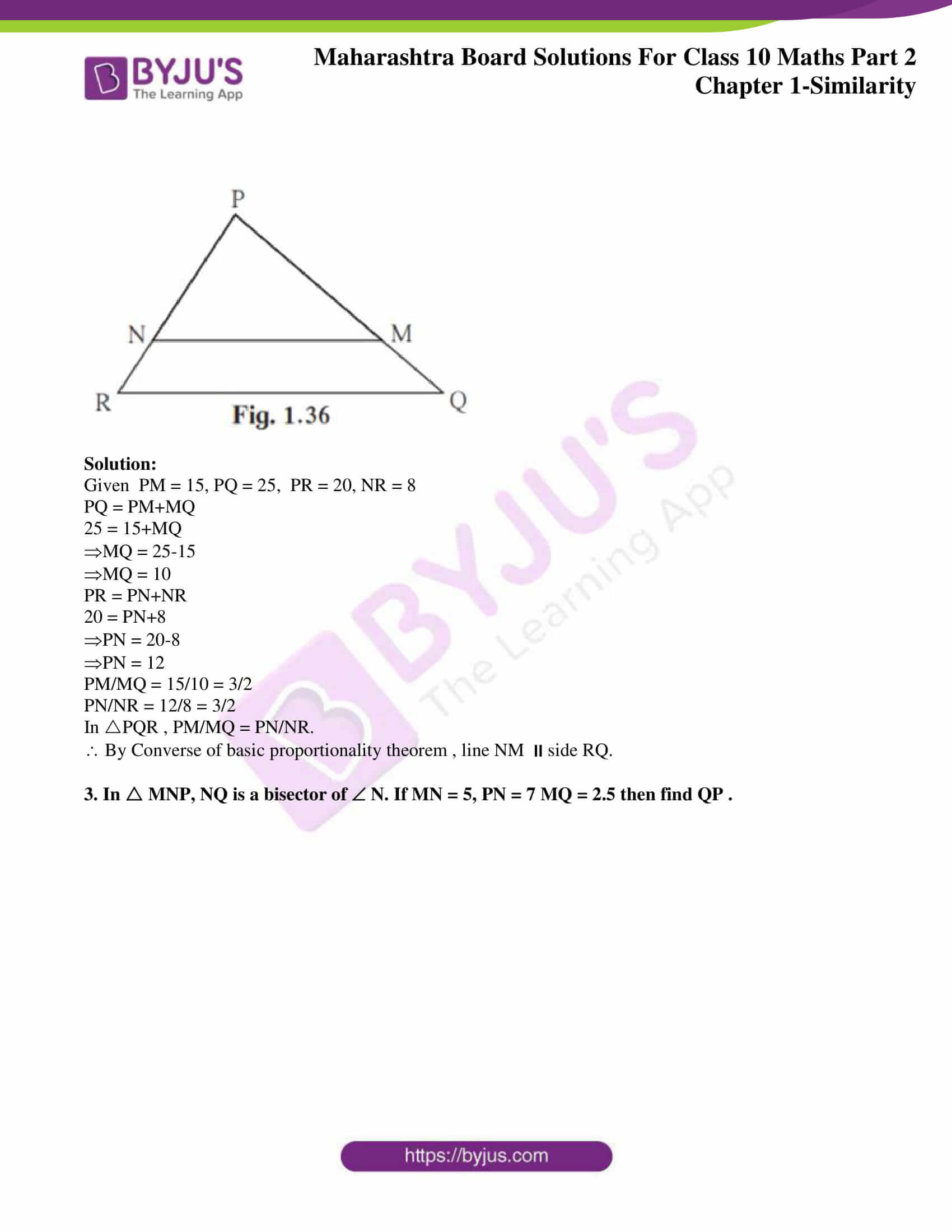
2. In PQR, PM = 15, PQ = 25 PR = 20, NR = 8. State whether line NM is parallel to side RQ. Give reason.
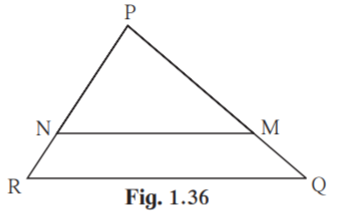
Solution:
Given PM = 15, PQ = 25, PR = 20, NR = 8
PQ = PM+MQ
25 = 15+MQ
MQ = 25-15
MQ = 10
PR = PN+NR
20 = PN+8
PN = 20-8
PN = 12
PM/MQ = 15/10 = 3/2
PN/NR = 12/8 = 3/2
In PQR , PM/MQ = PN/NR.
By Converse of basic proportionality theorem , line NM side RQ.
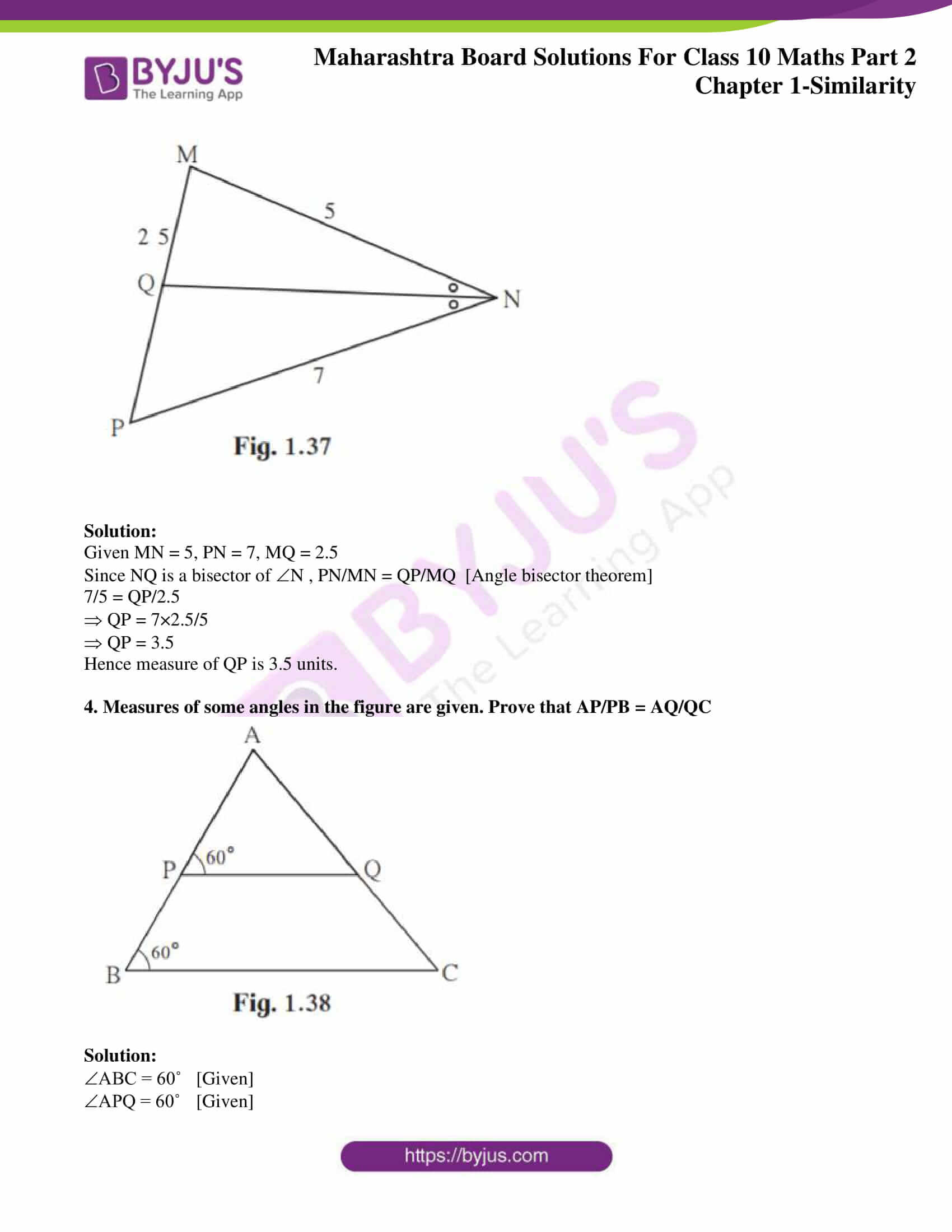
3. In MNP, NQ is a bisector of N. If MN = 5, PN = 7 MQ = 2.5 then find QP .
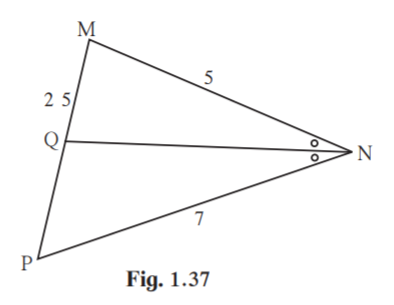
Solution:
Given MN = 5, PN = 7, MQ = 2.5
Since NQ is a bisector of N , PN/MN = QP/MQ [Angle bisector theorem]
7/5 = QP/2.5
QP = 7×2.5/5
QP = 3.5
Hence measure of QP is 3.5 units.
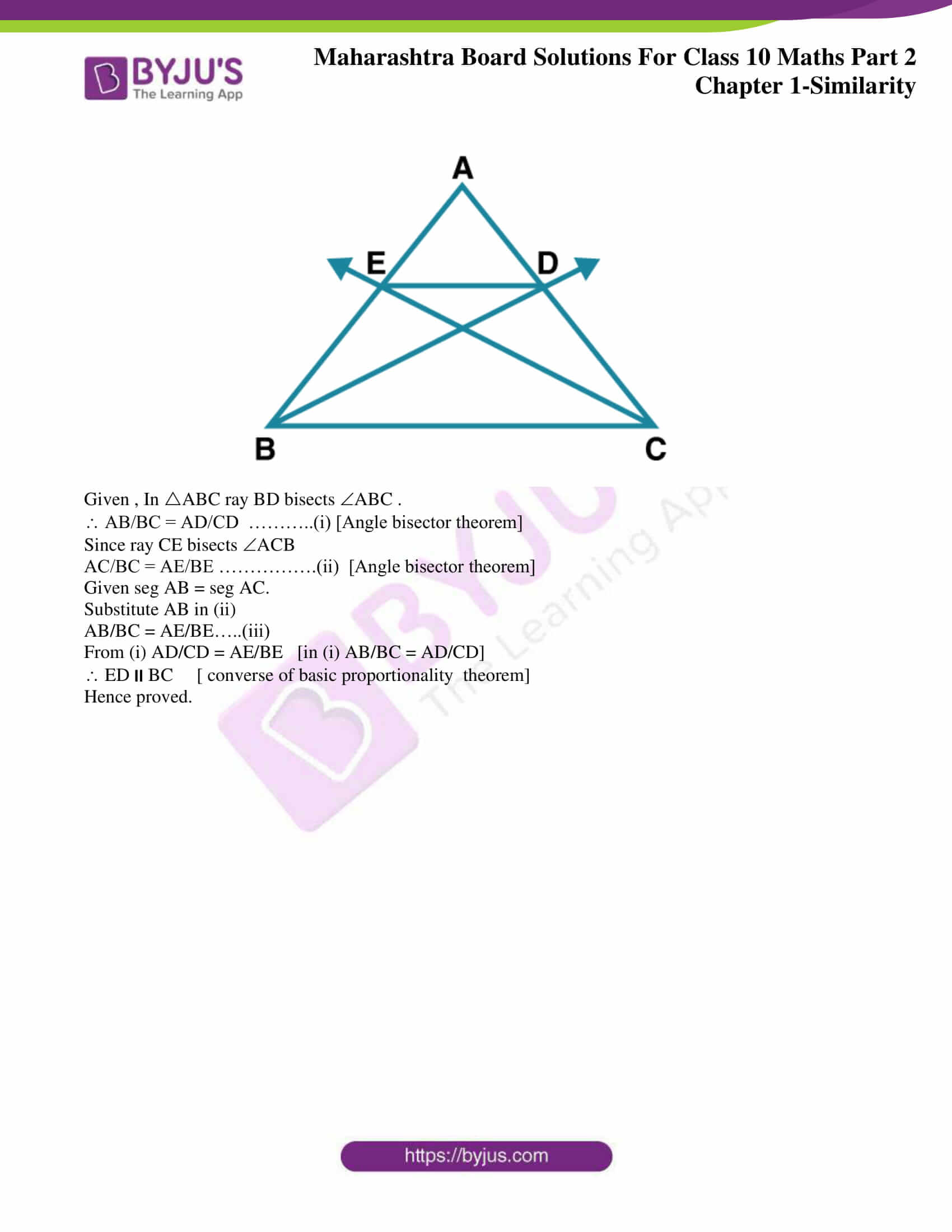
4. Measures of some angles in the figure are given. Prove that AP/PB = AQ/QC
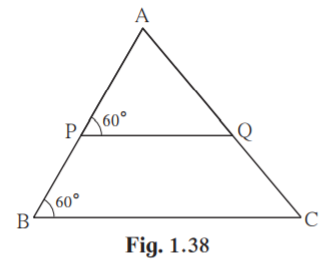
Solution:
ABC = 60˚ [Given]
APQ = 60˚ [Given]
Since the corresponding angles are equal, line PQBC.
In ABC , PQBC.
By basic proportionality theorem , AP/PB = AQ/QC
Hence proved.
5. In trapezium ABCD, side AB ||side PQ ||side DC, AP = 15, PD = 12, QC = 14, find BQ.
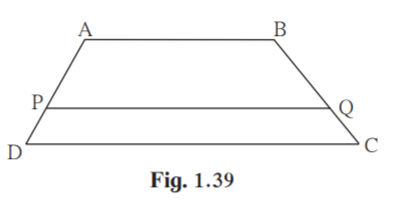
Solution:
Given ABPQDC.
AP = 15
PD = 12
QC = 14
AP/PD = BQ/QC [ Property of three parallel lines and their transversals]
15/12 = BQ /14
BQ = 15×14/12
BQ = 17.5 units.
Hence measure of BQ is 17.5 units.
6. Find QP using given information in the figure.
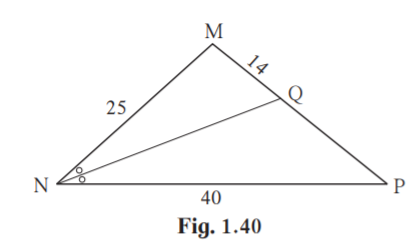
Solution:
From figure MN = 25, NP = 40, MQ = 14
Given NQ bisects MNP.
MN/NP = MQ/QP [Angle bisector theorem]
25/40 = 14/QP
QP = 40×14/25
QP = 22.5
Hence measure of QP is 22.5 units.
7. In figure 1.41, if AB || CD || FE then find x and AE.
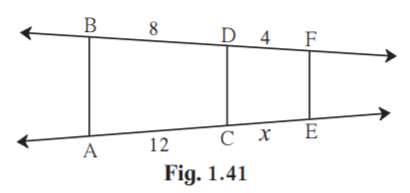
Solution:
From figure BD = 8, DF = 4, AC = 12 and CE = x
Given ABCDFE
BD/DF = AC/CE [Property of three parallel lines and their transversals]
8/4 = 12/x
x = 12×4/8
x = 6
CE = 6
AE = AC+CE
AE = 12+6
AE = 18
Hence measure of x is 6 units and AE is 18 units.
8. In D LMN, ray MT bisects LMN. If LM = 6, MN = 10, TN = 8, then find LT.

Solution:
Given ray MT bisects LMN.
LM = 6
MN = 10
TN = 8
Since ray MT bisects LMN , LM/MN = LT/TN [Angle bisector theorem]
6/10 = LT/8
LT = 6×8/10
LT = 4.8
Hence measure of LT is 4.8 units.
9. In ABC, seg BD bisects ABC. If AB = x, BC = x+5, AD = x-2, DC = x+2, then find the value of x.
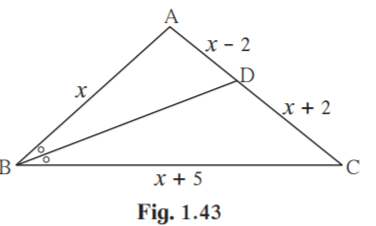
Solution:
Given BD bisects ABC.
Also AB = x, BC = x+5
AD = x-2, DC = x+2
Since BD bisects ABC, AB/BC = AD/DC [Angle bisector theorem]
x/(x+5) = (x-2)/(x+2)
Cross multiplying, we get
x(x+2) = (x+5)(x-2)
x2+2x = x2+5x-2x-10
x2+2x = x2+3x-10
x = 10
the value of x is 10 .
10. In the figure 1.44, X is any point in the interior of triangle. Point X is joined to vertices of triangle. Seg PQ || seg DE, seg QR || seg EF. Fill in the blanks to prove that, seg PR || seg DF.
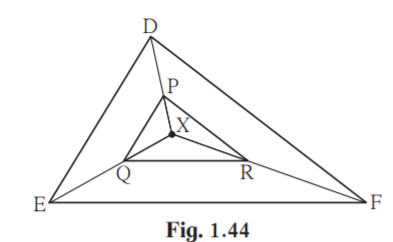
Proof : In XDE, PQ || DE ……..______
XP/_______ = ______/ QE ………. (I) (Basic proportionality theorem)
In XEF, QR || EF ………. _______
______ /______= ______ /______ ……….(II) ______
______ /______= ______ /______ ………. from (I) and (II)
seg PR || seg DE ………. (converse of basic proportionality theorem)
Solution:
In XDE, PQ || DE……. Given
XP/PD = XQ/QE…….. (I) (Basic proportionality theorem)
In XEF, QR || EF……. Given
XR/RF = XQ/QE……. .(II) (Basic proportionality theorem)
XP/PD = XR/RF ………. from (I) and (II)
seg PR || seg DE ………. (converse of basic proportionality theorem)
11*. In ABC, ray BD bisects ABC and ray CE bisects ACB. If seg AB seg AC then prove that ED || BC.
Solution:
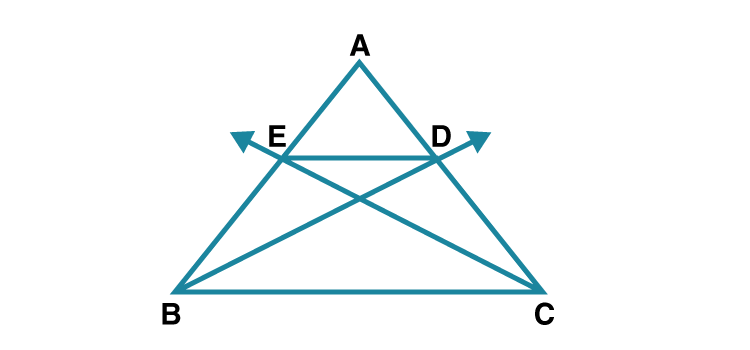
Given , In ABC ray BD bisects ABC .
AB/BC = AD/CD ………..(i) [Angle bisector theorem]
Since ray CE bisects ACB
AC/BC = AE/BE …………….(ii) [Angle bisector theorem]
Given seg AB = seg AC.
Substitute AB in (ii)
AB/BC = AE/BE…..(iii)
From (i) AD/CD = AE/BE [in (i) AB/BC = AD/CD]
EDBC [ converse of basic proportionality theorem]
Hence proved.
Practice set 1.3 Page 21
1. In figure1.55, ABC = 75°, EDC = 75° state which two triangles are similar and by which test? Also write the similarity of these two triangles by a proper one to one correspondence.

Solution:
Given ABC = 75˚ , EDC = 75˚
Consider ABC and EDC
ABC = EDC [Given ABC = 75˚ , EDC = 75˚]
ACB = DCE [Common angle]
ABC ~ EDC [AA test of similarity]
One to one correspondence is ABC↔ EDC
2. Are the triangles in figure 1.56 similar? If yes, by which test ?
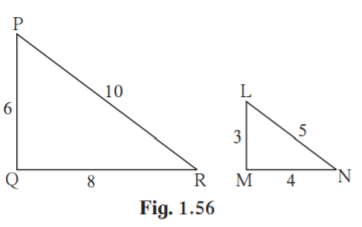
Solution:
Consider PQR and LMN ,
PQ/LM = 6/3 = 2/1 …………(i)
QR/MN = 8/4 = 2/1 ……….(ii)
PR/LN = 10/5 = 2/1 ……….(iii)
PQ/LM = QR/MN = PR/LN
PQR ~ LMN [SSS test of similarity]
3. As shown in figure 1.57, two poles of height 8 m and 4 m are perpendicular to the ground. If the length of shadow of smaller pole due to sunlight is 6 m then how long will be the shadow of the bigger pole at the same time ?
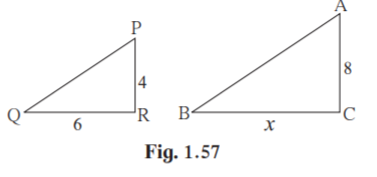
Solution:
Here PR and AC represents the smaller and bigger poles, and QR and BC represents their shadows respectively.
Given PR = 4m, QR = 6m , AC = 8m, BC = x
PRQ ~ ACB [ ∵Vertical poles and their shadows form similar figures]
PR/AC = QR/BC [ Corresponding sides of similar triangles]
4/8 = 6/x
x = 6×8/4
x = 12
Hence the length of shadow of the bigger pole is 12 m.
4. In ABC, AP ⊥ BC, BQ ⊥ AC B- P-C, A-Q – C then prove that, CPA ~ CQB. If AP = 7, BQ = 8, BC = 12 then find AC.
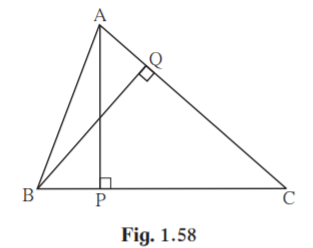
Solution:
Consider CPA and CQB,
CPA CQB [ From figure, angle is equal to 90˚]
PCA QCB [ Common angle]
CPA ~ CQB, [AA test of similarity]
Hence proved.
AC/BC = AP/BQ [ corresponding sides of similar triangles]
Given AP = 7, BQ = 8, BC = 12
AC/12 = 7/8
AC = 12×7/8
AC = 10.5
Hence measure of AC is 10.5 units.
5. Given : In trapezium PQRS, side PQ || side SR, AR = 5AP, AS = 5AQ then prove that, SR = 5PQ
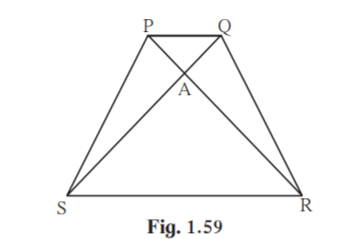
Solution:
Given side PQ side SR.
Also AR = 5AP, AS = 5AQ
SQ is the transversal of parallel sides PQ and SR.
QSR = PQS [ Alternate interior angles]
ASR = AQP….(i) [ Alternate interior angles]
Consider ASR and AQP
ASR = AQP From (i)
SAR = QAP [ vertical opposite angles]
ASR ~ AQP [ AA test of similarity]
AS/AQ = SR/PQ [ Corresponding sides of similar triangles]
AS = 5AQ [Given]
AS/AQ = 5/1
SR/PQ = 5/1
SR = 5PQ
Hence proved.
Practice set 1.4 Page 25
1. The ratio of corresponding sides of similar triangles is 3:5; then find the ratio of their areas
Solution:
When two triangles are similar, the ratio of areas of those triangles is equal to the ratio of the squares of their corresponding sides.
Given , the ratio of corresponding sides of the triangle is 3:5.
Ratio of their areas = 32/52 [Theorem of areas of similar triangles]
= 9/25
Hence ratio of their areas = 9:25
2. If ABC ~ PQR and AB: PQ = 2:3, then fill in the blanks.
A(ABC)/ A(PQR) = AB2/____ = 22/32 = ____/____
Solution:
A(ABC)/ A(PQR) = AB2/PQ2
= 22/32 = 4/9 [Theorem of areas of similar triangles]
3. If ABC ~ PQR, A( ABC) = 80, A( PQR) = 125, then fill in the blanks.
A( ABC) /A(… ) = 80/125 AB/PQ = ____/____
Solution:
Given A( ABC) = 80, A( PQR) = 125
( ABC) / A( PQR) = 80/125 = 16/25
( ABC) / A( PQR) = AB2/PQ2 [Theorem of areas of similar triangles]
AB2/PQ2 = 16/25
Taking square root on both sides
AB/PQ = 4/5
Hence AB/PQ = 4/5
4. LMN ~ PQR, 9 ×A(PQR ) = 16 ×A(LMN). If QR = 20 then find MN.
Solution:
Given 9 ×A(PQR ) = 16 ×A(LMN)
A(PQR )/ A(LMN) = 16/9…………(i)
LMN ~ PQR
A(PQR )/ A(LMN) = QR2/MN2 …..(ii)
From (i) and (ii)
QR2/MN2 = 16/9
Given QR = 20
202/MN2 = 16/9
Taking square root on both sides
20/MN = 4/3
MN = 20×3/4
MN = 15
Hence the measure of MN is 15 units.
Problem Set 1 Page 26
1. Select the appropriate alternative.
(1) In ABC and PQR, in a one to one correspondence AB/QR = BC/ PR = CA/ PQ then
(A) PQR ~ ABC
(B) PQR ~ CAB
(C) CBA ~ PQR
(D) BCA ~ PQR
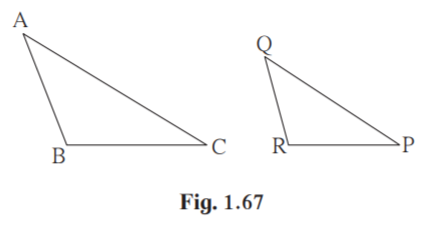
Solution:
Given AB/QR = BC/ PR = CA/ PQ
By SSS test of similarity , PQR ~ CAB .
Correct option is (B).
(2) If in DEF and PQR, D Q, R E then which of the following statements is
false?
(A) EF/PR = DF/ PQ
(B) DE/ PQ = EF/ RP
(C) DE/ QR = DF /PQ
(D) EF/ RP = DE/ QR
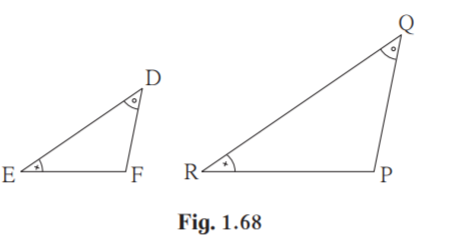
Solution:
Given D Q, R E
DEF ~QRP…. [AA test of similarity]
DE/QR = EF/RP = DF/QP [Corresponding sides of similar triangles]
DE/ PQ ≠ EF/ RP
Hence option (B) is false.
(3) In ABC and DEF B = E, F = C and AB = 3DE then which of the statements
regarding the two triangles is true?
(A)The triangles are not congruent and not similar
(B)The triangles are similar but not congruent.
(C)The triangles are congruent and similar.
(D) None of the statements above is true.
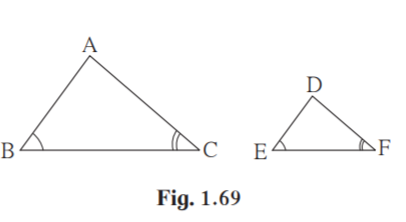
Solution:
Given B = E
F = C
ABC ~DEF [AA test of similarity]
Hence option B is the true statement.
(4) ABC and DEF are equilateral triangles, A (ABC):A(DEF)=1:2
If AB = 4 then what is length of DE?
(A)2√2
(B)4
(C)8
(D)4√2
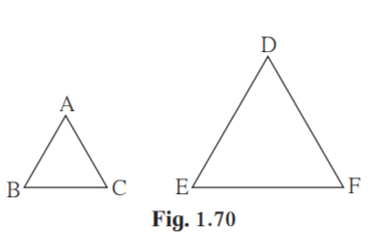
Solution:
Given A (ABC):A(DEF) = 1:2
ABC and DEF are equilateral triangles.
A = D [Angle equals 60˚]
B = E [Angle equals 60˚]
ABC ~ DEF [AA test of similarity]
A (ABC):A(DEF) = AB2/DE2 [Theorem of areas of similar triangles]
1/2 = 42/DE2
Taking square root on both sides
1/√2 = 4/DE
DE = 4√2
Hence option (D) is the correct answer.
(5) In figure 1.71, seg XY || seg BC, then which of the following statements is true?
(A) AB / AC = AX / AY
(B) AX / XB = AY / AC
(C) AX / YC = AY / XB
(D) AB / YC = AC / XB
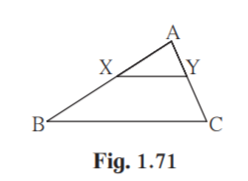
Solution:
Given seg XY || seg BC
AX/BX = AY/YC [Basic proportionality theorem]
(BX/AX ) +1 = (YC/AY) +1
(BX+AX)/AX = (YC+AY)/AY
AB/AX = AC/AY
AB/AC = AX/AY
Hence correct option is (A).
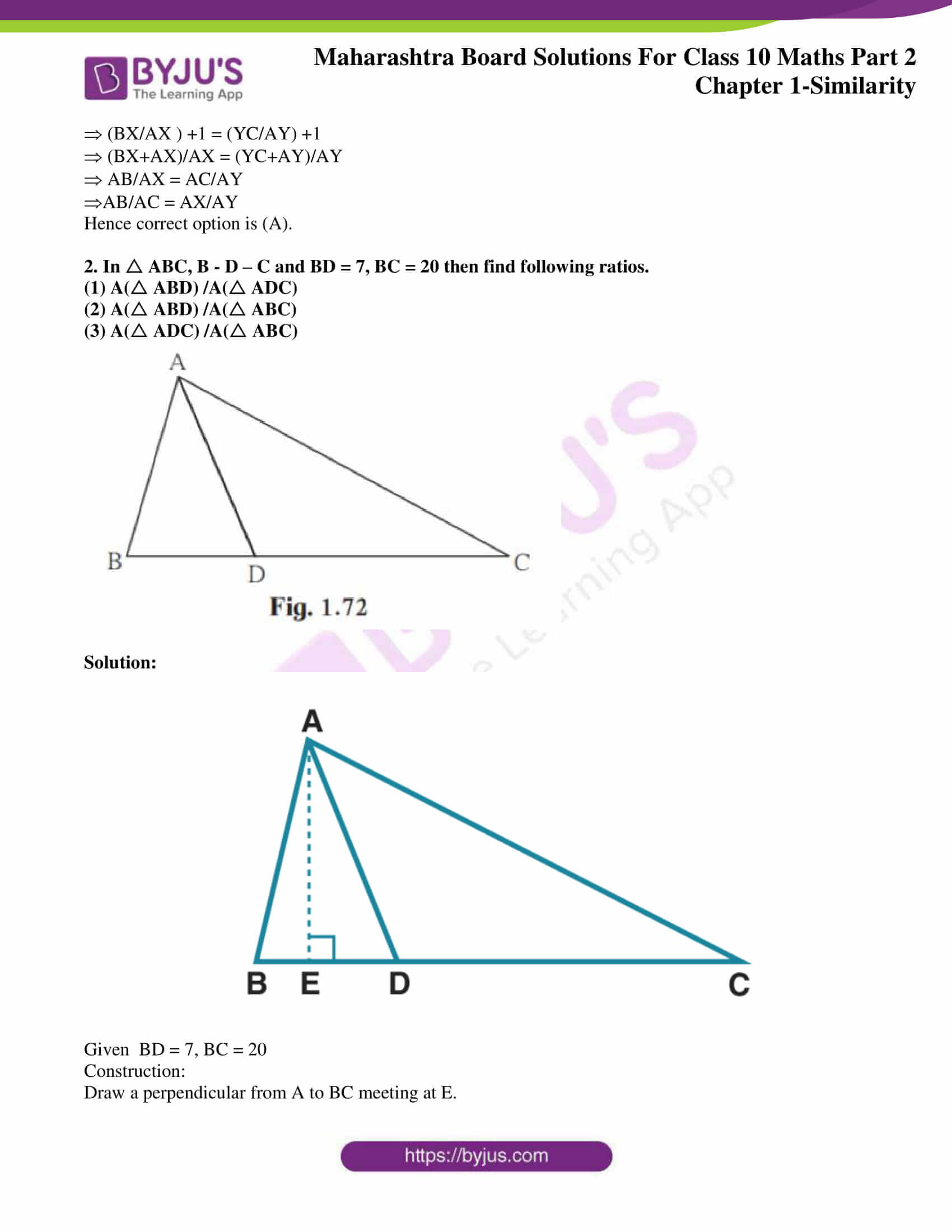
2. In ABC, B – D – C and BD = 7, BC = 20 then find following ratios.
(1) A( ABD) /A( ADC)
(2) A( ABD) /A( ABC)
(3) A( ADC) /A( ABC)
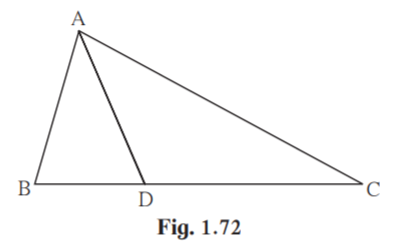
Solution:
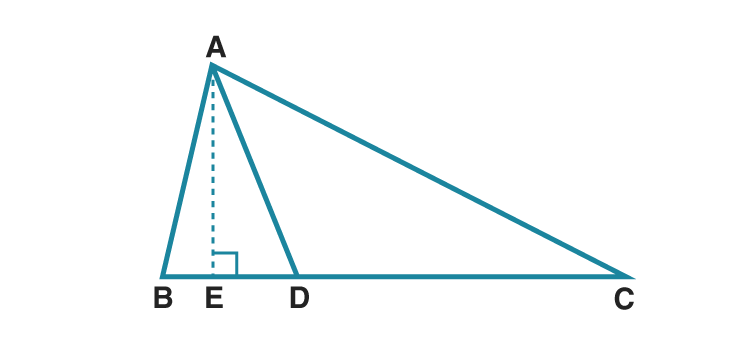
Given BD = 7, BC = 20
Construction:
Draw a perpendicular from A to BC meeting at E.
BC = BD+DC
20 = 7+DC
DC = 13
(1)A( ABD) /A( ADC) = BD/DC [Triangles having same height]
A( ABD) /A( ADC) = 7/13
(2) A( ABD) /A( ABC) = BD/BC [Triangles having same height]
A( ABD) /A( ABC) = 7/20
(3) A( ADC) /A( ABC) = DC/BC [Triangles having same height]
A( ADC) /A( ABC) = 13/20
3. Ratio of areas of two triangles with equal heights is 2:3. If the base of the smaller triangle is
6cm then what is the corresponding base of the bigger triangle ?
Solution:
Given ratio of two triangles with equal height is 2:3
Let b1 be base of smaller triangle and b2 be base of bigger triangle.
b1 = 6 cm
Let a1 and a2 be areas of the triangles.
Since triangles have equal height , a1/a2 = b1/b2
2/3 = 6/b2
b2 = 3×6/2
b2 = 9
Hence base of bigger triangle is 9 cm.
4. In figure 1.73, ABC = DCB = 90° AB = 6, DC = 8 then A( ABC) /A( DCB) = ?

Solution:
Given ABC = DCB = 90° AB = 6, DC = 8
BC is the common base of ABC and DCB
A( ABC) /A( DCB) = AB/DC
= 6/8
= 3/4
5. In figure 1.74, PM = 10 cm A(PQS) = 100 sq.cm A(QRS) = 110 sq.cm then find NR.
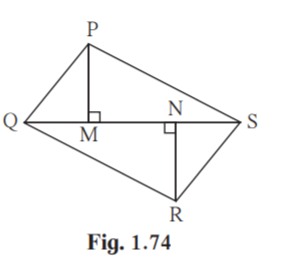
Solution:
Given PM = 10 cm
A(PQS) = 100 sq.cm
A(QRS) = 110 sq.cm
PQS and QRS have common base QS
A(PQS)/ A(QRS) = PM/NR
100/110= 10/NR
NR = 110×10/100
NR = 11
Hence NR = 11 cm.
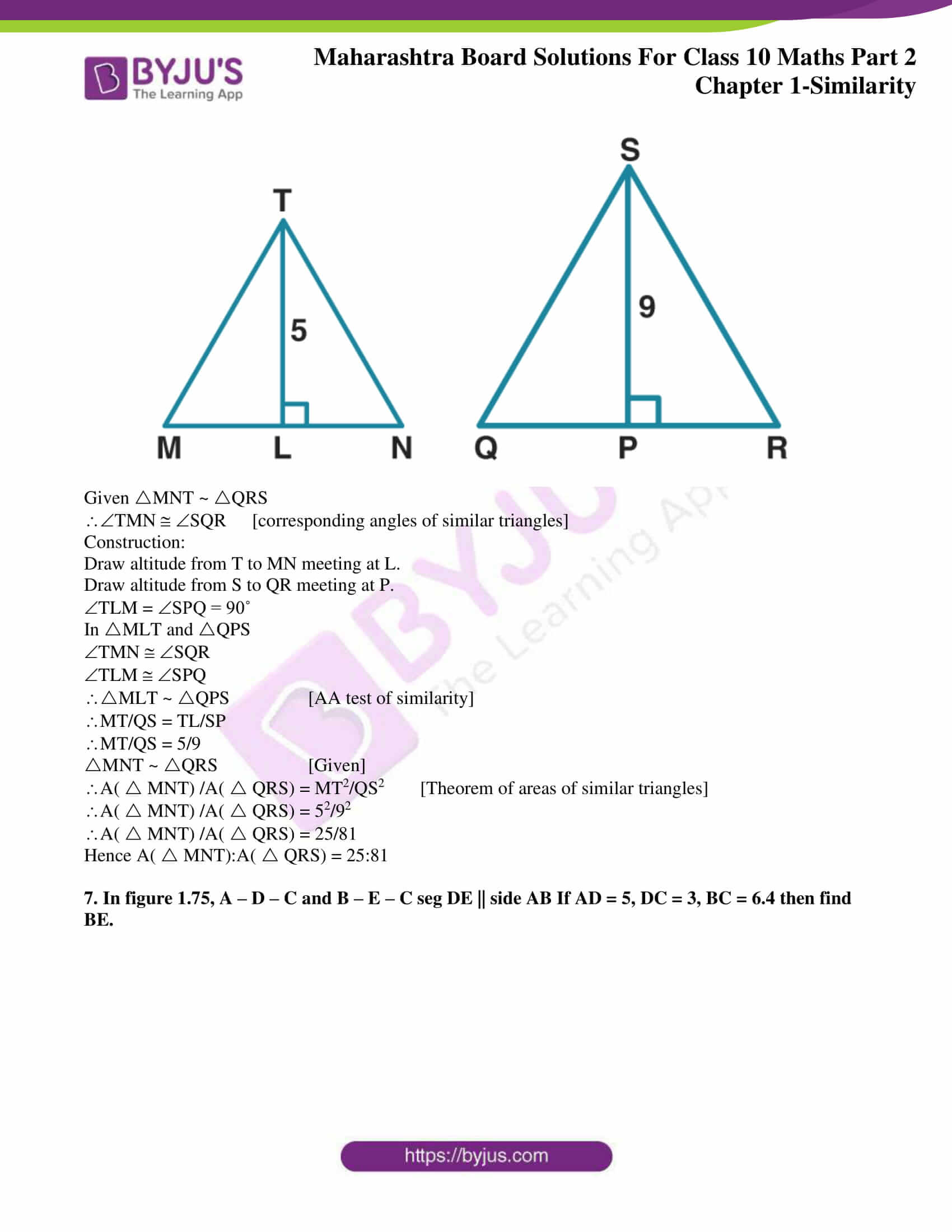
6. MNT ~ QRS. Length of altitude drawn from point T is 5 and length of altitude drawn
from point S is 9. Find the ratio A( MNT) /A( QRS) .
Solution:

Given MNT ~ QRS
TMN SQR [corresponding angles of similar triangles]
Construction:
Draw altitude from T to MN meeting at L.
Draw altitude from S to QR meeting at P.
TLM = SPQ = 90˚
In MLT and QPS
TMN SQR
TLM SPQ
MLT ~ QPS [AA test of similarity]
MT/QS = TL/SP
MT/QS = 5/9
MNT ~ QRS [Given]
A( MNT) /A( QRS) = MT2/QS2 [Theorem of areas of similar triangles]
A( MNT) /A( QRS) = 52/92
A( MNT) /A( QRS) = 25/81
Hence A( MNT):A( QRS) = 25:81
7. In figure 1.75, A – D – C and B – E – C seg DE || side AB If AD = 5, DC = 3, BC = 6.4 then find
BE.

Solution:
Given DE AB.
AD/DC = BE/EC [Basic proportionality theorem]
AD = 5, DC = 3, BC = 6.4 [Given]
BE = x , EC = 6.4-x [Given]
5/3 = x/(6.4-x)
Cross multiplying we get
5×(6.4-x) = 3× x
32-5x = 3x
32 = 8x
x = 32/8 = 4
Hence BE = 4 units.
In Class 10 Maths, Similarity is an important chapter where we learn AAA test, SAS test, AA test and SSS test for similarity of triangles. Also this chapter deals with basic proportionality theorem, property of angle bisector of a triangle and ratio of areas of two triangles.
Frequently Asked Questions on Maharashtra State Board Solutions for Class 10 Maths Part 2 Chapter 1 Similarity
Why are these Maharashtra State Board Class 10 Maths Part 2 Chapter 1 Solutions important?
Maharashtra State Board Class 10 Maths Part 2 Chapter 1 Solutions helps every student to easily comprehend the concept into their minds and clarify their doubts in a few seconds. The solutions are very self-explanatory and encourges the students to innovate and explore in Maths. Also, board exam aspirants can assess their learning abilities with these solutions.
How do we access these solutions?
The solutions are available are scrollable PDF online and the solutions and questions are also given directly on the webpage. We have also provided the PDF clickable links for those who wish to download the PDF format for future reference.
How to make the most of Maharashtra State Board Class 10 Maths Part 2 Chapter 1 Solutions?
Students are advised to refer to the questions from the Maharashtra State Board Class 10 Maths Part 2 Chapter 1 Solutions and solve them first before going back to check the answers. This will help the students to self analyse their preparation level and also to identify the mistakes, rectify them and avoid them for the exams. Timing the process also helps to manage time in a better way.





















Comments