In this article, we will discuss the speed of efflux, its calculation, Torricelli’s law, its derivation, venturimeter, its working principle and its working equation.
| Table of Contents |
Torricelli’s Law
As per Torricelli’s law for Newtonian fluids, the density of efflux of a fluid passing through a sharp-edged hole at the bottom of a tank filled with the fluid to a depth of h is the same as the speed that a body would acquire in a freely falling condition when falling from a height h.
Read More: Fluid Flow
Derivation
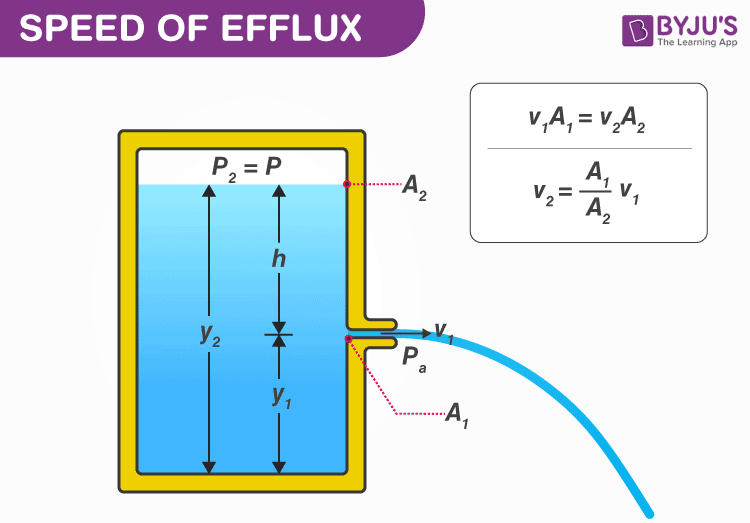
Consider a tank with a small hole in its side at a height y1 from the bottom, containing a liquid of density ρ. The air above the liquid is at pressure P, and its surface is at height y2.
From the equation of continuity, we can write
A1v1 = A2v2
Or v2 = A1v1/A2 ………………………….(1)
If the cross-sectional area of the tank A2 is much larger than that of the hole (A2 >>A1), then we may take the fluid to be approximately at rest at the top, i.e. v2 = 0. Now applying the Bernoulli equation at points 1 and 2 and noting that at the hole P1 = Pa (the atmospheric pressure), we have
Pa + 1/2ρv12+ ρgy1 = Pb + 1/2ρv22 + ρgy2 ……………………………(2)
Here, let the difference in the height = h (as shown in the figure) = y1-y2
From equations 1 and 2, we have
Read More: Bernoulli Principle
Venturimeter
Venturimeter is a flow measurement instrument. Here, a converging section of a pipe is used to increase the flow velocity and a corresponding pressure drop from which the flow rate of the fluid is deduced based on Bernoulli’s equation.
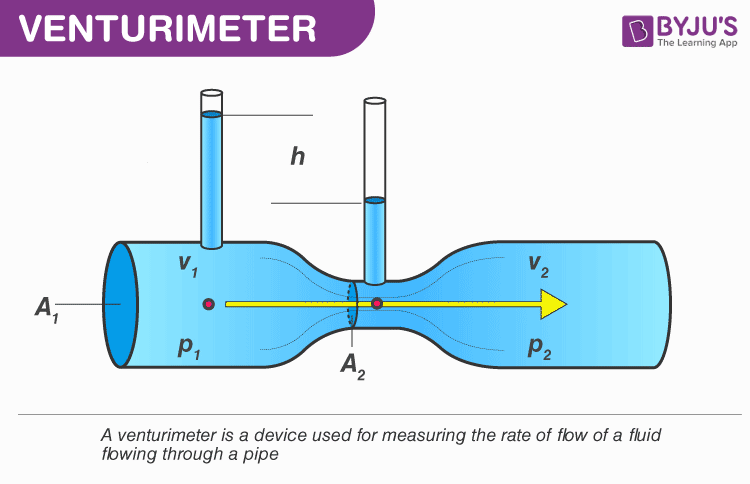
Let us consider the figure shown above. Here we can see the block diagram of a Venturimeter. Here we can see a small converging part, a throat and a diverging part. Here, we apply Bernoulli’s equation between the inline section and the throat section. The pressure difference is measured using a manometer.
P1 + 1/2ρV12 = P2 + 1/2ρV22
Where P1 is the pressure in the inline section and p2 is the pressure in the throat section, V1 is the velocity of the fluid passing through the inline section, and v2 and the velocity of the fluid passing through the throat section and ρ is the density of the liquid.
Now, from the equation of continuity, we can say
Volumetric flow rate = V = ¼ πD2u1 = ¼ πd2u2
Where V is the volumetric flow rate of the liquid, D is the diameter of the pipe, and d is the diameter of the throat.
Combining the two equations, we can write
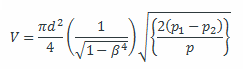
Where β is the ratio of diameters, d/D.
Here, we introduce a venture coefficient (C) considering the loss due to pipe friction and change in the total pressure,
Where Δp is the pressure difference and C is the coefficient of the Venturimeter.
Stay tuned with BYJU’S for more such interesting articles. Also, register to “BYJU’S – The Learning App” for loads of interactive, engaging Physics-related videos and unlimited academic assistance.
Understanding Continuity Equation


Good