Electromagnetic Waves

Electromagnetic waves were first postulated by James Clerk Maxwell and subsequently confirmed by Heinrich Hertz. Electromagnetic waves are created as a result of vibrations between an electric and a magnetic field. In this article, we will explore the definition and formation of electromagnetic waves along with the graphical and mathematical representations of electromagnetic waves in detail.

Table of Contents

What Are Electromagnetic Waves?

Electromagnetic waves are also known as EM waves. Electromagnetic radiations are composed of electromagnetic waves that are produced when an electric field comes in contact with the magnetic field. It can also be said that electromagnetic waves are the composition of oscillating electric and magnetic fields. Electromagnetic waves are solutions of Maxwell’s equations, which are the fundamental equations of electrodynamics.

Read More: Maxwell’s Equations

How Are Electromagnetic Waves Formed?

  • Generally, an electric field is produced by a charged particle. A force is exerted by this electric field on other charged particles. Positive charges accelerate in the direction of the field and negative charges accelerate in a direction opposite to the direction of the field.
  • The Magnetic field is produced by a moving charged particle. A force is exerted by this magnetic field on other moving particles. The force on these charges is always perpendicular to the direction of their velocity and therefore only changes the direction of the velocity, not the speed.
  • So, the electromagnetic field is produced by an accelerating charged particle. Electromagnetic waves are nothing but electric and magnetic fields travelling through free space with the speed of light c. An accelerating charged particle is when the charged particle oscillates about an equilibrium position. If the frequency of oscillation of the charged particle is f, then it produces an electromagnetic wave with frequency f. The wavelength λ of this wave is given by λ = c/f.  Electromagnetic waves transfer energy through space.

Graphical Representation of Electromagnetic Waves

Electromagnetic waves
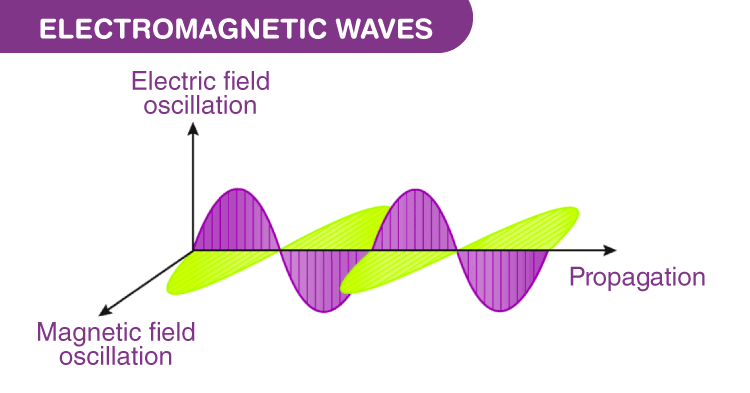
Electromagnetic waves are shown by a sinusoidal graph. It consists of time-varying electric and magnetic fields which are perpendicular to each other and are also perpendicular to the direction of propagation of waves. Electromagnetic waves are transverse in nature. The highest point of the wave is known as the crest while the lowest point is known as a trough. In vacuum, the waves travel at a constant velocity of 3 x 108 m.s-1.

Mathematical Representation of Electromagnetic Wave

A plane Electromagnetic wave travelling in the x-direction is of the form

\(\begin{array}{l}E(x,t)=E_{max}\cos (kx-\omega t+\Phi )\end{array} \)

\(\begin{array}{l}B(x,t)=B_{max}\cos (kx-\omega t+\Phi )\end{array} \)

In the electromagnetic wave, E is the electric field vector and B is the magnetic field vector.

Maxwell gave the basic idea of Electromagnetic radiations, while Hertz experimentally confirmed the existence of an electromagnetic wave.

The direction of propagation of the electromagnetic wave is given by the vector cross product of the electric field and magnetic field. It is given as:

\(\begin{array}{l}\vec{E}\times \vec{B}\end{array} \)
.

Read More: Magnetic Field

Electromagnetic Wave Equation

  • The electromagnetic wave equation describes the propagation of electromagnetic waves in a vacuum or through a medium.
  • The electromagnetic wave equation is a second-order partial differential equation.
  • It is a 3D form of the wave equation.
  • The homogeneous form of the equation is written as

\(\begin{array}{l}(\upsilon ^{2}_{ph}\bigtriangledown^{2}-\frac{\partial^2 }{\partial t^2})E=0\end{array} \)
\(\begin{array}{l}(\upsilon ^{2}_{ph}\bigtriangledown^{2}-\frac{\partial^2 }{\partial t^2})B=0\end{array} \)

Where,

\(\begin{array}{l}\upsilon _{ph}=\frac{1}{\sqrt{\mu \epsilon }}\end{array} \)

Intensity of an Electromagnetic Wave

\(\begin{array}{l}I=\frac{P}{A}=\frac{1}{2}c\epsilon _{0}E_{0}^{2}\\ \\ =\frac{1}{2}\frac{c}{\mu _{0}}B_{0}^{2}\end{array} \)

Speed of Electromagnetic Waves in Free Space

It is given by

\(\begin{array}{l}C=\frac{1}{\sqrt{(\mu _{0}\epsilon _{0})}}\end{array} \)

Where,

\(\begin{array}{l}\mu _{0}\end{array} \)
is called absolute permeability. Its value is
\(\begin{array}{l}1.257\times10^{-6}TmA^{-1}\end{array} \)

\(\begin{array}{l}\epsilon _{0}\end{array} \)
is called absolute permittivity. Its value is
\(\begin{array}{l}8.854\times 10^{-12}C^{2}N^{-1}m^{-2}\end{array} \)

C is the velocity of light in vacuum = velocity of electromagnetic waves in free space =

\(\begin{array}{l}3\times 10^{8}ms^{-1}\end{array} \)

Electromagnetic Spectrum

Electromagnetic Spectrum

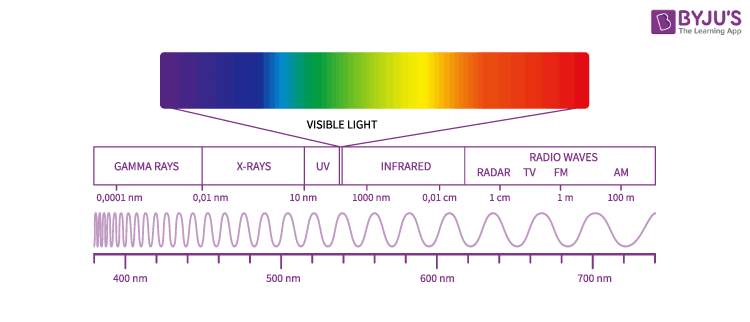
Electromagnetic waves are classified according to their frequency f or according to their wavelength

\(\begin{array}{l}\lambda =\frac{c}{f}.\end{array} \)

The wavelength ranges of different lights are as follows,

For visible light – approx. 400 nm to approx. 700 nm

For violet light – approx. 400 nm

For red light – approx. 700 nm

For more insights, stay tuned with BYJU ’s and fall in love with learning.

Applications of Electromagnetic Waves

Following are a few applications of electromagnetic waves:

  • Electromagnetic radiations can transmit energy in a vacuum or using no medium at all.
  • Electromagnetic waves play an important role in communication technology.
  • Electromagnetic waves are used in RADARS.
  • UV rays are used to detect forged bank notes. Real banknotes don’t turn fluorescent under UV light.
  • Infrared radiation is used for night vision and is used in security cameras.

Frequently Asked Questions

Q1

Name the property of an electromagnetic wave which is dependent on the medium in which it is travelling.

Velocity of an electromagnetic wave is a property which is dependent on the medium in which it is travelling. Other properties such as frequency, time period, and wavelength are dependent on the source that is producing the wave.

Q2

What is the wavelength of the photon of infrared light with the frequency 2.5 x 1014 Hz?

Since infrared light is a part of electromagnetic spectrum, the relation between the wavelength, frequency, and velocity is given by the formula:

\(\begin{array}{l}c=f\lambda\end{array} \)
Consider c = 3 x 108 m.s-1.
Substituting the values, we get wavelength = 1.2 x 10-6m.

Q3

State if the given statement is true or false: Radio waves and X-rays both are on the electromagnetic spectrum and can travel at the same speed.

The given statement is true. Any wave from the electromagnetic spectrum travels at a constant speed of light. Other properties such as frequency, energy, and wavelength vary depending on the type of wave and the source producing them. But the velocity remains constant.

Q4

What is the reason behind photons travelling at a speed of light while the other particles cannot?

Photons can travel at a speed of light while other particles cannot because they do not have mass.

Q5

State if the given statement is true or false: High frequency propagation is used so as to increase the accuracy.

The given statement is true. It is true that for increasing the accuracy, the frequency of propagation needs to be high.

Q6

What is the sequence for the propagation of electromagnetic waves?

The sequence for the propagation of electromagnetic waves is the generation, propagation, reflection, and reception.

Test Your Knowledge On Electromagnetic Waves!
Quiz Image

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz

Congrats!

Visit BYJU’S for all Physics related queries and study materials

Your result is as below

0 out of 0 arewrong
0 out of 0 are correct
0 out of 0 are Unattempted
PHYSICS Related Links
Doping Concentration Of Zener Diode Unit Of Force In Physics
Resonance Sheet Solution About Generator
State And Prove Bernoulli's Theorem Examples Of Refraction Of Light
Universal Law Of Gravitation Define Shm
Difference Between Thrust And Pressure Physics Project For Class 12 On Transformer

Comments

Leave a Comment

Your Mobile number and Email id will not be published.

*

*

  1.  Mithilesh
    April 13, 2022 at 2:02 am

    Very much helpful content is available on this site of Byjus

    Reply
  2. khushi
    May 17, 2022 at 2:02 pm

    exellent good help in study easy concept

    Reply