Maximum Power Transfer Theorem

The Maximum Power Transfer Theorem is one of the essential network theories. The maximum power transfer theorem helps us deduce the maximum external power generated with a finite internal resistance, in electrical circuit systems.

Table of Contents

What is the Maximum Power Transfer Theorem?


Maximum Power Transfer Theorem explains that to generate maximum external power through a finite internal resistance (DC network), the resistance of the given load must be equal to the resistance of the available source.

In other words, the resistance of the load must be the same as Thevenin’s equivalent resistance.

In the case of AC voltage sources, maximum power is produced only if the load impedance’s value is equivalent to the complex conjugate of the source impedance.

Maximum Power Transfer Formula

As shown in the figure, a dc source network is connected with variable resistance RL.


Maximum Power Transfer Theorem

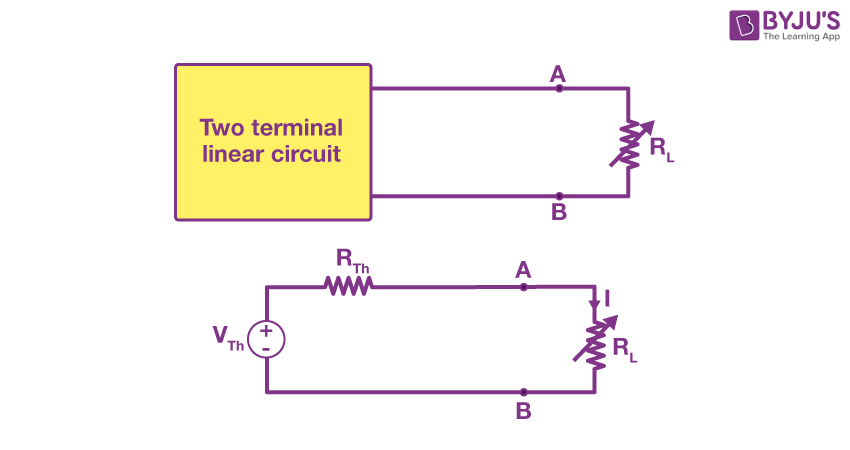
The fundamental Maximum Power Transfer Formula is

\(\begin{array}{l}P_{max} = \frac{V_{Th}^{2}}{4R_{Th}}\end{array} \)


The video below explains the concept of Maximum Power Transfer Theorem in detail.

Maximum Power Transfer Theorem Proof

The Maximum Power Transfer Theorem aims to figure out the value RL, such that it consumes maximum power from the source.

\(\begin{array}{l}\mathit{I}=\frac{V_{Th}}{R_{Th}+R_{L}} \end{array} \)

The total power connected to the resistive load,

\(\begin{array}{l}\mathit{P_{L}}=\mathit{I^{2}}\mathit{R_{L}}=\left ( \frac{V_{Th}}{R_{Th}+R_{L}} \right )^{2}\times R_{L}\end{array} \)

PL can be maximized by adjusting RL, therefore highest power can be generated when
(dPL/dRL) =0

But,

\(\begin{array}{l}\frac{dP_{L}}{dR_{L}}= \frac{1}{\left [\left (R_{Th}+R_{L} \right )^2 \right ]^{2}}\left [ \left ( R_{Th}+R_{L} \right )^2 \frac{d}{dR_{L}}\left ( V^2_{Th}R_{L} \right )-V^2_{Th}R_{L}\frac{d}{dR_{L}}\left ( R_{Th}+R_{L} \right )^2\right ]\end{array} \)
 
 
\(\begin{array}{l}=\frac{1}{\left ( R_{Th}+R_{L} \right )^4}\left [ \left (R_{Th}+R_{L} \right )^2V^2_{Th}-V^2_{Th}R_{L}\times 2(R_{Th}+R_{L}) \right ]\end{array} \)
 

\(\begin{array}{l}=\frac{V^2_{Th}\left ( R_{Th}+R_{L}-2R_{L} \right )}{\left ( R_{Th}+R_{L} \right )^3}=\frac{V^2_{Th}\left ( R_{Th}-R_{L} \right )}{\left ( R_{Th}+R_{L} \right )}\end{array} \)
 
 
\(\begin{array}{l}\frac{dP_{L}}{dR_{L}}=0\end{array} \)
 
 
\(\begin{array}{l}\frac{V^2_{Th}\left ( R_{Th}-R_{L} \right )}{\left ( R_{Th}+R_{L} \right )^3}=0\end{array} \)
 
 
\(\begin{array}{l}\left ( R_{Th}-R_{L} \right )=0\end{array} \)
 
 

\(\begin{array}{l}R_{Th}=R_{L}\end{array} \)

So, the highest power transmitted to the load resistance is,

\(\begin{array}{l}P_{max} = \frac{V_{Th}^{2}}{4R_{Th}}\end{array} \)

Application of Maximum Power Transfer Theorem

The presence of linked sources enables the network to be active, so the Maximum Power Transfer Theorem is applied for active networks & passive networks.

  • Maximum Power Transfer Theorem can also be implemented to linear networks, the network system, along with R, L, C, & restrained linear sources as elements.
  • Maximum power transfer theorem functions only when there is a variable load. If not, choose the least available internal sources of impedance, which paves in maximum current through the fixed load. Consequently, maximum power is expelled by the load circuit.
  • Large sound systems are built around this process. Maximum power transfer is generated in the circuit by making the speaker’s (load) resistance equivalent to the resistance of the amplifier. Once the speaker and amplifier have equal resistance, both are considered harmonised.
  • Another application is on the relationship between the starter motor and the battery of a car engine. Power applied to the starter will rely on the effectual resistance of the motor and battery resistance. When their values are equal, the highest power will be transmitted to kickstart the engine.

Related Links


Frequently Asked Questions – FAQs

Q1

What is the Maximum Power Transfer Theorem? Explain with an example.

Maximum Power Transfer Theorem explains that to generate maximum external power through a finite internal resistance (DC network), the resistance of the given load must be equal to the resistance of the available source.
Large sound systems are built around this process. Maximum power transfer is generated in the circuit by making the speaker’s (load) resistance equivalent to the resistance of the amplifier.
Once the speaker and amplifier have equal resistance, both are considered harmonised.

Q2

Does the Maximum Power Transfer Theorem apply to AC circuits?

Just like DC circuits, AC circuits work under the Maximum Power Transfer Theorem. But in contrast to DC circuits, resistance is swapped with impedance in AC electric circuits.

Q3

What is the Maximum Power Transfer Formula?

When

\(\begin{array}{l}R_{Th}=R_{L}\end{array} \)
Then
\(\begin{array}{l}P_{max} = \frac{V_{Th}^{2}}{4R_{Th}}\end{array} \)

Q4

What is Thevenin’s Resistance?

Thevenin’s Resistance is the resistance calculated at the given terminals with every voltage source reinstated with short circuits, and every current source replaced by open circuits.

Q5

What are the limitations of the Maximum Power Transfer Theorem?

The critical limitation of the Maximum Power Transfer Theorem is, it cannot be used in nonlinear and unilateral networks. As efficiency drops to 50%, it is also not applicable in power systems.

Watch the video and learn to solve problems based on Maximum Power Transfer Theorem.

Stay tuned to BYJU’S and Fall in Love with Learning!

PHYSICS Related Links
Convex Lens Examples Voltage Units
Moment Of Inertia Units Diamagnetic Elements
Difference Between Refrigeration And Air Conditioning Define Electromagnet
Physics Diagram How To Make A Water Clock?
Different Types Of Resistors Conductors And Insulators Examples

Comments

Leave a Comment

Your Mobile number and Email id will not be published.

*

*