You must have observed that even though molecules in a gas have high-speed ranging in the order of the speed of sound, yet a gas leaking from a cylinder in a kitchen takes considerable time to diffuse to the other corners of the room, the smell of garbage does not spread too far from its source or the fragrance of an essence stick takes some time to fill the room. This happens because molecules in a gas have a finite though the small size, so they are bound to undergo collisions. As a result, they cannot move straight unhindered; their paths keep getting incessantly deflected. In this section, we will learn more about the concept of the mean free path and its mathematical formulation.
| Table of Contents |
Mean Free Path
It is the average distance travelled by a moving particle between two successive impacts in a system of agitated particles, which results in the change in their energy, physical properties, or direction of motion.
Molecules of gas are considered to be spheres of diameter d. We will focus on a single molecule that is moving with an average speed v.
From the image shown above, we can say that it will suffer a collision with many molecules coming in its path. Let us say in time Δt, it sweeps a volume πd2vΔt wherein any other molecule will collide with it. Here, if n is the number of molecules per unit volume, the molecules will suffer nπd2vΔt collisions in the given time Δt.
The time between two successive collisions is given by,
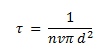
The average distance between two successive collisions, called the mean free path l is given by:
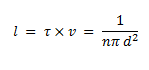
Factors affecting mean free path
Some mean free path factors are mentioned in the points below.
- Density: As the density increases, the molecules come closer to each other, thus increasing the number of collisions, and decreasing the mean free path.
- Number of molecules: As the number of molecules increases the probability of collision increases and thus the mean free path decreases.
- Radius of the molecule: As the radius of the molecule increases the space between the molecules decreases causing the number of collisions to increase, thus decreasing the mean free path.
- Pressure, temperature, and other physical factors also affect the density of the gas and thus affect the mean free path.
To learn more about mean free path and other related topics, download BYJU’S-The Learning App.
Frequently Asked Questions – FAQs
What is mean free path?
What are the factors that affect the mean free path?
- Density: As the density increases, the molecules come closer to each other, thus increasing the number of collisions, and decreasing the mean free path.
- Number of molecules: As the number of molecules increases the probability of collision increases and thus the mean free path decreases.
- Radius of the molecule: As the radius of the molecule increases the space between the molecules decreases causing the number of collisions to increase, thus decreasing the mean free path.
- Pressure, temperature, and other physical factors also affect the density of the gas and thus affect the mean free path.
What is the unit of molar mass?
What are the assumptions of the kinetic theory of gases?
- The molecules do not interact with each other.
- The collision of molecules with themselves or walls will be an elastic collision.
- The momentum is conserved.
- Kinetic energy will be conserved.
Give a daily life example of refraction of light.
What is the formula for the time between two successive collisions?
What is the significance of the Kinetic Theory of Gases
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
Comments