Scalar products and vector products are two ways of multiplying two different vectors which see the most application in physics and astronomy. The scalar product of two vectors is defined as the product of the magnitudes of the two vectors and the cosine of the angles between them.
| Table of Contents |
Scalar Product
“Scalar products can be found by taking the component of one vector in the direction of the other vector and multiplying it with the magnitude of the other vector”. It can be defined as:
Scalar product or dot product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number.
This can be represented as follows:
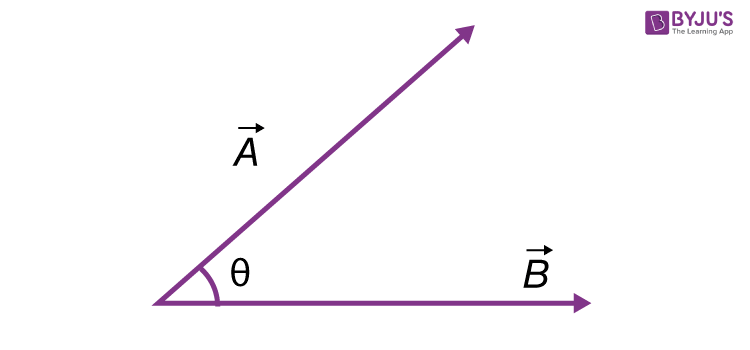
- \(\begin{array}{l}\vec{A}\,denotes\,the\,vector\end{array} \)
- \(\begin{array}{l}A\,denotes\,the\,magnitude\,of\,vector\, \vec{A}\end{array} \)
The scalar product is also termed as the dot product or inner product and remember that scalar multiplication is always denoted by a dot.
If the same vectors are expressed in the form of unit vectors i, j and k along the axis x, y and z respectively, the scalar product can be expressed as follows:
Where,
- \(\begin{array}{l}\vec{A}=A_{X}\hat{i}+A_{Y}\hat{j}+A_{Z}\hat{k}\end{array} \)
- \(\begin{array}{l}\vec{B}=B_{X}\hat{i}+B_{Y}\hat{j}+B_{Z}\hat{k}\end{array} \)
Read More: Scalar Product
Matrix Representation of Scalar Products
It is useful to represent vectors as row or column matrix, instead of as the above unit vectors. If we treat vectors as column matrices of their x, y and z components, then the transposes of these vectors would be row matrices.
Vector Product
The magnitude vector product of two given vectors can be found by taking the product of the magnitudes of the vectors times the sine of the angle between them. It can be defined as:
Vector product or cross product is a binary operation on two vectors in three-dimensional space.
The magnitude of the vector product can be represented as follows:
Remember the above equation is only for the magnitude, for the direction of the vector product, the following expression is used,
[The above equation gives us the direction of the vector product]
Vector Products Represented by Determinants
Now the above determinant can be solved as follows:
Application of scalar and vector products are countless especially in situations where there are two forces acting on a body in a different direction.
Example:
Calculation of the magnetic force acting on a moving charge in a magnetic field, other applications include determining the net force on a body.
Read More: Magnetic Field
Frequently Asked Questions – FAQs
Define the scalar product of two vectors.
What is the scalar product also known as?
The scalar product is also known as the dot product or inner product.
Define vector product.
How is the magnitude of the vector product represented?
How is the scalar product represented?
Stay tuned to BYJU’S and Fall in Love with Learning!
Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!
Select the correct answer and click on the “Finish” button
Check your score and answers at the end of the quiz
Visit BYJU’S for all Physics related queries and study materials
Your result is as below
Comments