RBSE Maths Class 8 Chapter 6: Important Questions and Solutions

RBSE Maths Chapter 6 – Polygons Class 8 Important questions and solutions can be accessed here. The important questions and solutions of Chapter 6, available at BYJU’S, contain detailed step by step explanations. All the questions solved on this page are based on the new pattern prescribed by the RBSE. Students can also get the syllabus, textbooks and additional questions on RBSE Class 8 solutions.

Chapter 6 of the RBSE Class 8 Maths will help the students to solve problems related to diagonal of a polygon, concave and convex polygon, regular and irregular polygons, the sum of the measure of exterior angles of a polygon, characteristic of a quadrilateral, different types of quadrilaterals, special cases of a parallelogram.

RBSE Maths Chapter 6: Exercise 6.1 Textbook Important Questions and Solutions

Question 1: Draw the diagonal for the following figures and answer the questions given below.

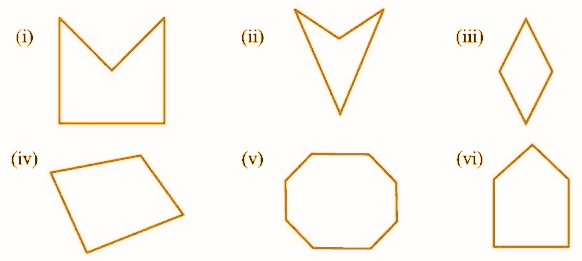
[viii] In which of the above shapes, the diagonal is outside the polygon?

[ix] Check whether the given polygons are concave or convex.

Solution:

Convex figures: (iii), (iv), (v), (vi).

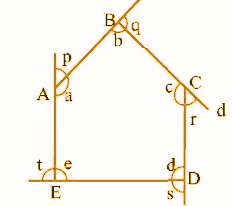
Question 2: Write the

[i] interior angles and

[ii] exterior angles of the given polygon ABCDE.

Question 3: Define a regular polygon. Write the names of the regular polygons with

[i] 5 sides

[ii] 6 sides

[iii] 8 sides

Solution:

A polygon is said to be a regular polygon if all the angles and sides are equal [otherwise it is an irregular polygon].

Question 4: Solve for unknown angles in the figures given below.

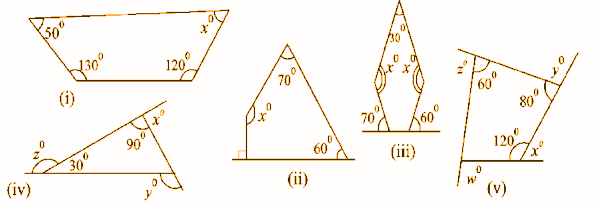
The given angles are

x^o + 50^o + 120^o + 130^o = 360^o

x^o + 300^o = 360^o

x^o = 360^o – 300^o

x^o = 60^o

The given angles are

x^o + 70^o + 60^o + 90^o = 360^o

x^o + 220^o = 360^o

x^o = 360^o – 220^o

x^o = 140^o

The sum of the interior angles of a pentagon = 180^o * [5 – 2] = 180^o x 3 = 540^o

The given angles are

2x^o + 30^o + [180^o – 70^o] + [180^o – 60^o] = 540^o

2x^o + 30^o + 110^o + 120^o = 540^o

2x^o + 260^o = 540^o

2x^o = 540^o – 260^o

x^o = [280^o] / 2

x^o = 140^o

The sum of the angles of a triangle = 180^o

30^o + 90^o + [180^o – y] = 180^o

120^o + 180^o – y = 180^o

300^o – y = 180^o

y = 120^o

x + 90^o = 180^o

x = 90^o

z + 30^o = 180^o

z = 150^o

x = 180^o – 120^o

x = 60^o

y + 80^o = 180^o

y = 180^o – 80^o

y = 100^o

z + 60^o = 180^o

z = 120^o

The sum of the interior angles of a quadrilateral = 360^o

180^o – w + 120^o + 60^o + 80^o = 360^o

440^o – w = 360^o

w = 440^o – 360^o

w = 80^o

Question 5: What is the number of sides of a regular polygon whose measure of each exterior angle is 45^o?

Solution:

Let the number of sides be x.

The sum of all exterior angles of a ‘x’ sided regular polygon = 360^o

Each exterior angle = [360^o] / n

45^o = [360^o] / n

n = [360^o] / [45^o]

n = 8

Hence, the number of sides is 8.

Question 6: What is the number of sides of a regular polygon whose measure of each interior angle is 165^o?

Solution:

Let the number of sides be x.

Each interior angle = 165^o

So, each exterior angle = 180^o – 165^o = 15^o

The sum of all exterior angles of a ‘x’ sided regular polygon = 360^o

Each exterior angle = [360^o] / n

15^o = [360^o] / n

n = [360^o] / [15^o]

n = 24

Hence, the number of sides is 24.

Question 7: What is the number of sides of a regular polygon whose measure of each exterior angle is 24^o?

Solution:

Let the number of sides be x.

The sum of all exterior angles of a ‘x’ sided regular polygon = 360^o

Each exterior angle = [360^o] / n

24^o = [360^o] / n

n = [360^o] / [24^o]

n = 15

Hence, the number of sides is 15.

Question 8: Find the value of each interior angle of a regular polygon of 10 sides.

Solution:

n = 10 [number of sides]

Each interior angle of ‘n’ sided regular polygon

= {[n – 2] * 180^o} / [n]

= {[10 – 2] * 180^o} / [10]

= {[8] * 180^o} / [10]

= 1440 / 10

= 144^o

The value of each interior angle of a regular polygon of 10 sides is 144^o.

Question 9: If the interior angle of any polygon is 115^o, then will it be a regular polygon?

Solution:

Each interior angle of ‘n’ sided regular polygon = {[n – 2] * 180^o} / [n]

115^o = {[n – 2] * 180^o} / [n]

115^o x n = {[n – 2] * 180^o}

115^o x n = 180^o (n – 2)

115^o x n = 180^o x n – 360^o

115^o x n = 180^o x n – 360^o

360^o = (180^o – 115^o) n

360^o / 65^o = n

n = 5.54

It is not a whole number.

Hence, it will not be a regular polygon.

Question 10: One interior angle of a hexagon is 165^o and the measure of the remaining interior angle is x^o. Find the measure of all the angles.

Solution:

The sum of interior angles of a hexagon = (n – 2) * 180^o = (6 – 2) * 180^o = 4 * 180^o = 720^o

165^o + x^o + x^o + x^o + x^o + x^o = 720^o

165^o + 5x^o = 720^o

5x^o = 720^o – 165^o

5x^o = 555^o

x^o = 555^o / 5

x^o = 111^o

Question 11: By increasing the sides of a triangle in a single direction, obtained exterior angles are 110^o, 115^o and x^o. Find the value of x.

Solution:

The sum of all exterior angles of a regular polygon = 360^o

110^o + 115^o + x^o = 360^o

225^o + x^o = 360^o

x^o = 360^o – 225^o

x = 135^o

Question 12: Find the sum of all interior angles of a regular heptagon.

Solution:

The sum of interior angles of a heptagon

= (n – 2) * 180^o

= (7 – 2) * 180^o

= 5 * 180^o

= 900^o

RBSE Maths Chapter 6: Exercise 6.2 Textbook Important Questions and Solutions

Question 1: Fill in the blanks choosing the right option.

(i) Adjacent angles of a parallelogram are ……… (equal/supplement).

(ii) Diagonals of a rectangle are ……… (equal/perpendicular bisector).

(iii) In any trapezium AB || CD, If A = 100° then the value of D will be ……….. (100⁰/80^o).

(iv) If in any quadrilateral, diagonals bisect each other on a right angle then, it is called ……… (parallelogram/rhombus).

(v) All squares are…….. (congruent/similar).

Solution:

(i) supplementary (ii) equal (iii) 80° (iv) rhombus (v) similar

Question 2: In the figure below, BEST is a parallelogram. Find the values of x, y and z.

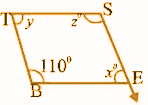
BEST is a parallelogram.

∠B + x^o = 180^o

In a parallelogram, adjacent angles are supplementary.

110^o + x^o = 180^o

x^o = 180^o – 110^o

x^o = 70^o

In a parallelogram, opposite angles are equal.

x^o = y^o

y^o = 70^o

110^o = z^o

z = 110^o

Question 3: Find the values of x, y and z in the following parallelograms.

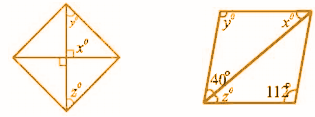
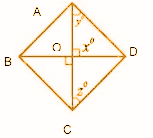
In △OAD, OA = AD

∠OAD = ∠ODA = y^o

∠AOD + ∠OAD + ∠ODA = 180^o [Because sum of the angles of a triangle is 180^o.]

90^o + y^o + y^o = 180^o

2y^o = 90^o

y^o = 45^o

Since the diagonals of a parallelogram bisect each other,

OA = AC

OA = AD

OC = OD

∠DOC = 90^o

z^o = 45^o

40° + z^o + y° = 180° [ As the adjacent angles of a parallelogram are supplementary]

40° + z^o + 112° = 180°

z^o = 180° – 152^o

z = 28^o

x^o + y^o + 40° = 180^o [As the sum of angles of a triangle is 180^o.]

x^o + 112° + 40^o = 180°

x^o + 152^o = 180°

x^o = 180^o – 152°

x^o = 28^o

Question 4: In any parallelogram, the ratio of two adjacent angles is 1:5. Find the value of all the angles of a parallelogram.

Solution:

According to the question, let ABCD be a parallelogram.

∠A : ∠B = 1:5

Since the sum of two adjacent angles of a parallelogram is 180°

∠A + ∠B = 180^o

Sum of Ratio = 1 + 5 = 6

Hence, ∠A = [⅙] * 180^o = 30°

∠B = [⅚] * 180^o = 150^o

Since, the opposite angles of a parallelogram are equal,

∠C = ∠A = 30^o and ∠D = ∠B= 150°

Angles of a parallelogram are 30°,150°, 30° and 150°.

Question 5: Given below are two parallelograms RISK and STEW. Find the values of x and y [length in cm].

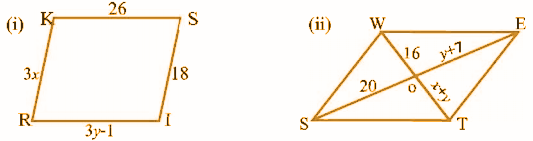
(i) The opposite sides of a parallelogram are equal.

3x = 18 and 3y – 1 = 26

x = 6 and 3y = 26 + 1

3y = 27

y = 9

So. x = 6 cm and y = 9 cm.

(ii) The diagonals of a parallelogram bisect each other

x + y = 16 …………(1) and y + 7 = 20 ……… (2)

From equation (2), y = 20 – 7 = 13

Puting y = 13 in equation (1) x + 13 = 16

So. x = 3 and y = 13 cm.

Question 6: The rectangle HOPE is given below. Its diagonals intersect each other at the point S. Find the value of x if SH = 2x + 4 and SE = 3x + 1.

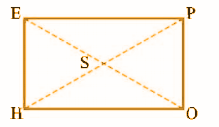
We know that the diagonals of a rectangle bisect each other.

SE = SO and SH = SP

EO = 2SE = 2 (3x + 1) and HP = 2 SH = 2 (2x + 4)

Since the diagonals of a rectangle are equal,

EO = HP

2 (3x + 1) = 2 (2x + 4)

3x + 1 = 2x + 4

3x – 2x = 4 -1

x = 3

Question 7: Given PEAR is a rhombus. Find the values of x, y and z. Also, write the causes.

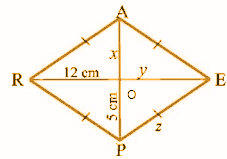
In a rhombus, the diagonals bisect each other.

OA = OP

Given that OP = 5 cm, OE = OR and OR = 12cm.

x = 5 cm

y = 12 cm

As the sides of a rhombus are equal, EP = PR

z = 13 cm.

Question 8: In the given trapezium PQRS, PQ || SR. Find the angles x and y.

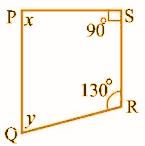
Given that PQ || SR

x + 90^o = 180^o

x = 90^o

Therefore PQRS is a quadrilateral.

x + y + 130^o + 90^o = 360^o

The sum of all angles of a quadrilateral = 360⁰

90^o + y + 130°+ 90^o = 360^o

310^o + y =360^o

y = 360^o – 310

y = 50^o

RBSE Maths Chapter 6: Additional Questions and Solutions

Question 1: A concrete slab was made by a mason and he wants it to be rectangular in shape. In what different ways can it be made a rectangular?

Solution:

The concrete slab will be rectangular in shape if the following is ensured:

• The opposite sides should be equal.

• The diagonals should be equal.

• Each angle should measure 90°.

Question 2: A square is defined as a rectangle with equal sides. Is it possible that a rhombus of equal angles be defined? Explain.

Solution:

It is not possible to define a square as a rhombus with equal angles as the diagonals will not be equal unless every angle is a right angle [90^o].

Question 3: Is it possible that a trapezium will have all sides and angles equal? Explain.

Solution:

In the case of a trapezium, it is not possible to have all angles equal as its opposite sides become parallel. A trapezium is a quadrilateral in which a pair of sides are parallel. It cannot have all sides equal as its opposite sides become parallel.

Question 4: Find the measure of each of the angles of a parallelogram in which two adjacent angles of a parallelogram are equal.

Solution:

Let the measures of the 2 adjacent angles be P and Q.

The adjacent angles of a parallelogram are supplementary.

∠P + ∠Q = 180^o

x + x =180^o

2x = 180^o

x = 90^o

Therefore, ∠P = ∠Q = 90^o

Since, the opposite angles of a parallelogram are equal, ∠P = ∠Q = ∠R = ∠S = 90^o.