A pyramid with a polygonal base and triangular faces equal to the number of sides in the base. In a pyramid, the triangular faces meet at a single point known as the apex. The base of the pyramid is connected with the faces of the pyramid. Since each and every triangular face will have different size and shape, we would need to find the area of each using the formula given.
The different types of pyramid are given as:
- Square Pyramid
- Triangular Pyramid
- Pentagonal Pyramid
- Hexagonal Pyramid
Square Pyramid Area Formula
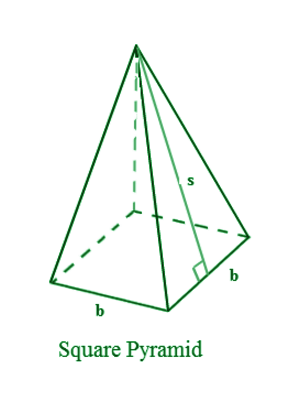
| Surface Area of a Square Pyramid | A = 2 x b × s + b2 |
Triangular Pyramid Area Formula

| Surface Area of a Triangular Pyramid | A =1⁄2(a × b) + 3⁄2(b × s) |
Pentagonal Pyramid Area Formula

| Surface Area of a Pentagon Pyramid | A =5⁄2(a × b) + 5⁄2(b × s) |
Hexagonal Pyramid Area Formula

| Surface Area of a Hexagonal Pyramid | A =3(a × b) + 3(b × s) |
Solved Example
Question: Find out the Surface area of the square pyramid with side 5 cm and base 4 cm
Solution:
Surface area of a square pyramid = 2bs + b2
Here, using the formula= 2 x 4 x 5 + 42 = 40 + 16 = 56 cm2
| More topics in Surface Area of a Pyramid Formula |
| Surface Area of a Square Pyramid Formula |
Comments