Uniform Circular Motion Formula

What is uniform circular motion?

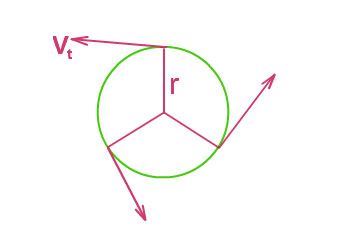
The term circular is applied to describe the motion in a curved path. The motion of an object along a circular path covering equal distance along the circumference in the same interval of time is known as uniform circular motion. In any uniform circular motion, the speed remains constant, but the direction of the velocity changes.

The tangential speed at every point on the circumference is found to be constant in a uniform circular motion, and the tangential velocity vector is tangent at every point over the circumference.

Tangential velocity is the vector formed to the tangential speed; therefore, the magnitude remains constant and equal to the tangential speed of the uniform circular motion.

The Tangential speed of the uniform circular motion is given by,

v = 2π r / T

The centripetal acceleration  is given by,

Where,

v= tangential velocity

R= radius

T= period (Time required to make one complete circle)

a= centripetal acceleration

Any object moving in uniform circular motion also has an angular velocity.

The object’s velocity changes continuously and therefore there is an acceleration in the circular motion, and this acceleration is always directed towards the center of the circle which is termed as centripetal acceleration.  

Solved Numericals

Example 1

A racer is moving with a constant tangential speed of 50 m/s, takes one lap around a circular track in 40 seconds. Calculate the magnitude of the acceleration of the car.

Solution:

Given:

Speed v = 50 m/s

T = 40 seconds.

We know that,

Acceleration, 

T = 2 π r / v

Therefore, r = Tv / 2π

When both the formulas are combined, we get

a = v2 / (Tv/2 π) = v / (T/2 π)

  = 50 /[ 40 / 6.28]

a = 7.86  

Example 2:

An object moving in a circular motion has a centripetal acceleration of 20 m/s2. If the radius of the motion is 0.5 m, calculate the frequency of the motion.

Solution:

Given:

Acceleration = 20 m/s²

Radius = 0.5 m

We know that

20 =  / 0.5

v = 3.16 m/s

v = 2 πr / t

3.16 =(2)(3.14)(0.5)/t

3.16 =3.14 / t

T = 1.006

Frequency,f= 1/t = 1/1.006

Therefore, f = 0.99 Hz

For more such valuable equations and formulas stay tuned with BYJU’S!!