Volume of a Pyramid Formula
In geometry, a pyramid is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle called a lateral face. The volume of a pyramid is the measure of the number of units occupied by the pyramid.
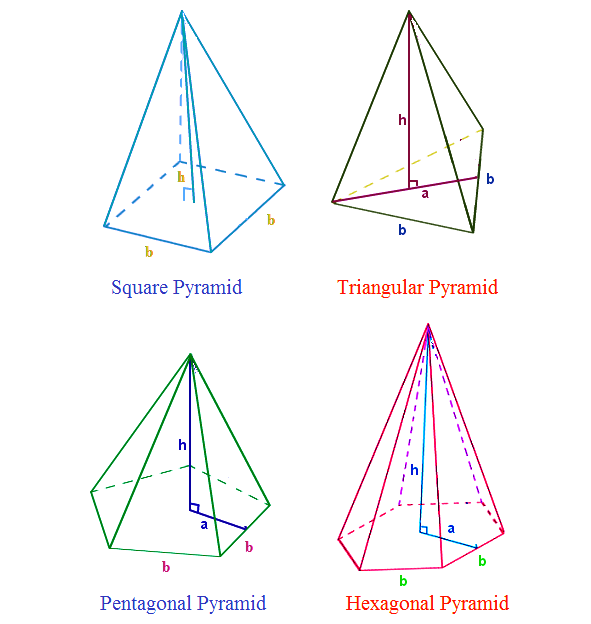
The Volume of a Pyramid Formula is given as,
\[\large Volume\;of\;a\;square\;pyramid=\frac{1}{3}b^{2}h\]
\[\large Volume\;of\;a\;triangular\;pyramid=\frac{1}{6}abh\]
\[\large Volume\;of\;a\;pentagonal\;pyramid=\frac{5}{6}abh\]
\[\large Volume\;of\;a\;hexagonal\;pyramid=abh\]
Where,
a – apothem length of the pyramid
b – base length of the pyramid
h – height of the pyramid
Volume of a Pyramid Formula Solved Example
Example: A pyramid has a square base of side 4 cm and a height of 9 cm. Find its volume.
Solution:
Given,
b = 4 cm
h = 9 cm
So, the volume is
| More topics in Volume of a Pyramid Formula | |
| Volume of a Square Pyramid Formula | |
Comments