Ellingham Diagram -Thermodynamics of Metallurgy

Gibbs equation helps us to predict the spontaneity of a reaction on the basis of enthalpy and entropy values directly. H.G.T Ellingham proposed the Ellingham diagram to predict the spontaneity of reduction of various metal oxides. Ellingham diagram was basically a curve which related the Gibbs energy value with the temperature. Gibbs energy is given as:

ΔG = ΔH – TΔS

Where ΔH is the change in enthalpy and ΔS is the change in entropy.

With respect to a reaction, Gibbs energy can be related to the equilibrium constant as:

ΔG^o= – RTlnK

Where K is the equilibrium constant.

Thus, when the reaction is exothermic, enthalpy of the system is negative, thus making Gibbs free energy negative. Hence, we can say that the reaction will proceed in the forward direction due to a positive value of the equilibrium constant. This law can be scaled for two different reactions taking place in a system too.  The overall reaction (combination of two reactions) will occur if and only if net ΔG (sum of ΔG’s of both the reactions) of the two possible reactions is negative.

Ellingham diagram for Reduction of Oxides:

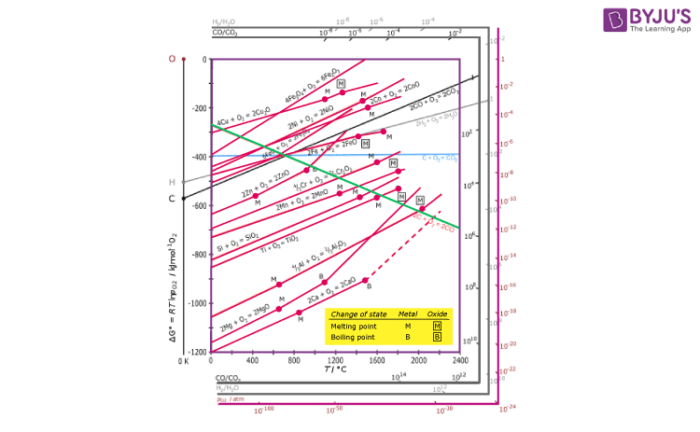
1. Ellingham diagram is a plot between Δ_fG^o and T for the formation of oxides of metals. A general reaction expressing oxidation is given by:

2xM(s) + O₂(g) → 2M_xO(s)

As is evident from the reaction, the gaseous amount of reactant is decreasing from left to right as the product formed is solid metal oxide on the right side. Hence, we can say that molecular randomness is also decreasing from left to right. Thus, ΔS is negative and ΔG shifts towards higher side despite rising T. Hence, for most of the reactions shown above for the formation of M_xO (s), the curve is positive.

2. Except for the processes in which change of phase takes place, each plot is a straight line. This temperature at which change of phase takes place is indicated by a positive increase in the slope. For example, the melting is indicated by an abrupt change in the curve in Zn, ZnO plot.
3. The metal oxide (M_xO) is stable at the point in a curve below which ΔG is negative. Above this point, the metal oxide is unstable and decomposes on its own.
4. Feasibility of reductions of the oxide of the upper line by the element represented by the lower line is determined by the difference in the two Δ_rG⁰ values after the point of intersection in the Ellingham diagram.

To learn more about Ellingham diagrams download BYJU’S – The Learning App.