Homogeneous Equilibrium

We encounter so many reactions around us in our day-to-day life; the rusting of iron, the burning of paper, the souring of curd, the formation of ozone, etc. Many of these reactions involve the presence of components in different phases, such as solid iron coming in contact with gaseous oxygen to form solid iron oxide, which we know as rust. Similarly, gaseous hydrogen combines with gaseous oxygen to form liquid water. Dealing with such reactions is a tedious task. If the components are in the same phase, the interaction of the components can be understood easily, while when the components are in different phases, the interaction gets more complicated.

Introduction to Homogeneous equilibrium

In order to simplify the problems and understand the concept, we divide such reactions into different categories, namely, the homogeneous reactions, where the components involved in the reaction are present in the same phase and the heterogeneous reactions, where the components involved are present in different phases. The methods of dealing with both the reactions are different and so is the determination of the equilibrium state. In this section, we will learn about a homogeneous equilibrium and the calculation of the equilibrium constant for a homogeneous reaction.

Equilibrium Constant for Homogeneous Reaction

Let us consider a homogeneous system, given by the following reaction

Here, we see that gaseous nitrogen reacts with gaseous hydrogen to form gaseous ammonia. Let us now calculate the equilibrium constant for the above reaction.

In terms of the molar concentration of the components in the reaction, we can write

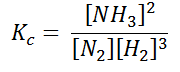
As we know, for reactions involving gases, we express the equilibrium concentration in terms of partial pressure.

Using the ideal gas equation,

Where P is the pressure of the system, V is the volume of the system, n is the number of moles of components present in the system, R is the universal gas constant and T is the temperature of the system.

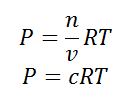
Here, c is the concentration of the system. We can also write it as,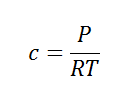

So equilibrium constant can also be written as,

Here, we note that the general expression for K_c and K_p can be written as,

Where Δn is defined as the number of moles of gaseous products – the number of moles of gaseous reactants.

Recommended Videos

To learn more about homogeneous equilibrium, heterogeneous equilibrium, and other related topics, register with BYJU’S and download BYJU’S – The Learning App.