In the case of k-way set associative mapping, the cache lines get grouped into various sets where all the individual sets consist of k number of lines. Here, a certain main memory block can map to only a particular cache set. However, within this very set, the memory block can be mapped to a freely available line of cache.
In this article, we will take a look at the K-way Set Associative Mapping according to the GATE Syllabus for CSE (Computer Science Engineering). Read ahead to learn more.
Table of Contents
What is K-way Set Associative Mapping?
The K-way set associative mapping is like a mix of fully associative and direct mapping. Here,
- The total number of sets = The total number of lines/K
- K refers to the K-way set associative
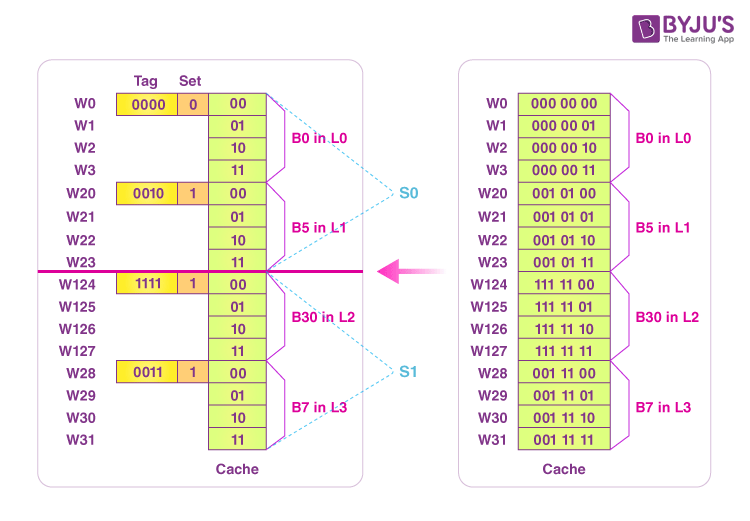
- K= 23 for a 2-way set associative
- The total number of sets = 4/2 or 2 sets (S1, S0)

The blocks mentioned above would be in which lines? We calculate it by the K MOD N formula. In this case, “K” refers to the Block Number, while “N” refers to the total number of sets in a cache.
For instance,
- In case the Block Number = 0, (0 MOD 2) would be = 0. Now, it means that Block 0 would be in Set 0.
- Also, in case the Block Number = 7, (7 MOD 2) would be = 1. Now, it means that Block 7 would be in Set 1.
- While in case the Block Number =10, (10 MOD 4) would be = 0. Now, it means that Block 10 would be in Set 0.
Thus,
One of these blocks would be in the S1 (set one) in the line L3 or L2 at any time B1, B3,………., B29, B31
One of these blocks would be in the S0 (set zero) in the line L1 or L0 at any time B0, B2,……, B28, B30
Physical Address
In case a cache has 4 lines, and we consider a 2-way set associative, then:

Here, we search for a certain block through the tag (leading to Cache Hit or Cache miss).
Now, suppose that the CPU generates the 0011000 address for a main memory of 128-word.
Here, the first two (00) bits represent the Block offset, and the next bit (0) is used to represent the set number. Also, the last 4 bits (0011) would represent the Tag in the Cache memory.
Since the tag bits of the CPU address do not match with the tag bits of a line of the S0 Set, it is a case of a cache miss.
Numerical Problems
The formula for K-way is as follows:
- Physical address = set + tag + block offset
- The comparator value in the case of a k-way set associative would be = (k-value) – (tag bit). For example, (7-8) would mean that the 7 lines of a certain set are compared with the 8-bits of a tag.
1. When the cache is 64 kilobytes in size and the size of Block/line is 8 bytes, how many bits would be required in order to represent the lines of a 4-way set-associative memory in cache?
Answer – Total number of lines = Size of Cache / Size of Block = 64 kilobytes / 8 bytes = 213 bytes
Thus, 13 bits are required in order to represent various lines in the cache.
The total number of bits for a set = Total number of lines / K-way = 213 bytes / 22 = 211
Thus, a total number of 11 bits are required in order to represent various sets in a cache.
2. In case there are 10 bits for a given set in a 4-way set-associative where the block size happens to be 16 kilobytes, then the cache size would be:
Answer – K-set associative cache size = number of sets x total number of lines per set x size of line.
Size of cache = 210 x 4 x 214 bytes = 64 megabytes
3. A certain 4-way set associative memory that has a 16KB capacity is built with about 8 words of block size. Here, the word length would be 32 bits. The total size of the space of the physical address is 4 gigabytes. Find the number of bits for a Tag field.
Answer – Block size = 4 Bytes × 8 = 32 Bytes = 25 Bytes
Total number of Sets in the cache = Cache Size / Block Size x K-way = 4 kilobytes / 25B x 4 = 27 Bytes
Space of Physical Address = 4 gigabytes = 232 bytes
Thus, according to the formula:
Space of Physical Address = Total number of sets + Tag + Size of Block
232 Bytes = 27 Bytes + Tag + 25 Bytes
Tag = 220 Bytes
Thus, 20 Bits are required in order to represent a tag number.
Pros and Cons
Pros: The comparison time is reduced in the K-way set associative mapping as compared to the fully associative mapping.
Cons: It involves the factor of conflict miss.
For example,
The person who lives in a single room indicates direct mapping. It’s because it is very easy for someone to find this person, but there’s a restriction for them to not at all move anywhere. On the other hand, fully associative mapping means a person could be easily living anywhere in India. So, the searching time is increased here, but the restriction is removed. Thus, k-way tells that a person can be living in any state in this country.
Keep learning and stay tuned to get the latest updates on GATE Exam along with GATE Eligibility Criteria, GATE 2023, GATE Admit Card, GATE Syllabus, GATE Previous Year Question Paper, and more.
Also Explore,
- Types of Instructions in Computer Architecture
- ALU (Arithmetic Logic Unit)
- Control Unit
- Microprogrammed Control Unit
- Instruction Formats
- Addressing Modes
- Memory Hierarchy
- Fully Associative Mapping
- Direct Mapping
- Conversion of Bases to Other Bases
- Flynn’s Classification of Computers
- SIMD
- SISD
- MIMD
- MISD
- De Morgan’s Theorems
Comments