Selina Solutions Concise Mathematics Class 6 Chapter 14 Fractions discusses the concepts related to Fractions, with illustrations for better learning. Subject experts have solved the questions clearly for every exercise. The solutions prepared in a simple language help to increase logical thinking among students. Selina Solutions is a key resource, which provides answers to all the queries of the students. Frequent practice of textbook problems is a must, for those who aspire to score more marks in the exams. Students can download the Selina Solutions Concise Mathematics Class 6 Chapter 14 Fractions PDF, from the below available links.
Chapter 14 of Selina Solutions explains basic topics like types of fractions and conversion of fractions. Various shortcut methods are also available to help students in grasping the concepts effortlessly, within a short duration.
Selina Solutions Concise Mathematics Class 6 Chapter 14: Fractions Download PDF
Exercises of Selina Solutions Concise Mathematics Class 6 Chapter 14: Fractions
Access Selina Solutions Concise Mathematics Class 6 Chapter 14: Fractions
Exercise 14(A)
1. For each expression, given below, write a fraction:
(i) 2 out of 7 = ………
(ii) 5 out of 17 = …….
(iii) three-fifths = …….
Solution:
(i)The fraction for 2 out of 7 is written as 2 / 7
(ii) The fraction for 5 out of 17 is written as 5 / 17
(iii) The fraction for three-fifths is written as 3 / 5
2. Fill in the blanks:
(i) 5 / 8 is …………. fraction
(ii) 8 / 5 is ………. fraction
(iii) -15 / -15 is …………fraction
(iv) The value of 5 / 5 = ………..
(v) The value of 5 / -5 = ………….
Solution:
(i) 5 / 8 is proper fraction
(ii) 8 / 5 is improper fraction
(iii) -15 / -15 is improper fraction
(iv) The value of 5 / 5 = 1
(v) The value of 5 / -5 = -1
3. From the following fractions, separate:
(i) Proper fractions
(ii) Improper fractions:
2 / 9, 4 / 3, 7 / 15, 11 / 20, 20 / 11, 18 / 23 and 27 / 35
Solution:
(i) A fraction whose numerator is less than denominator is known as proper fractions
The proper fractions are 2 / 9, 7 / 15, 11 / 20, 18 / 23 and 27 / 35
(ii) A fraction whose numerator is greater than denominator is known as improper fractions
The improper fractions are 4 / 3 and 20 / 11
4. Change the following mixed fractions to improper fractions:
(i) 
(ii)
(iii)
(iv) 
Solution:
(i)
The conversion of mixed fraction to an improper fraction is shown below
= (2 × 5 + 1) / 5
= (10 + 1) / 5
= 11 / 5
(ii)
The conversion of mixed fraction to an improper fraction is shown below
= (3 × 4 + 1) / 4
= (12 + 1) / 4
= 13 / 4
(iii)
The conversion of mixed fraction to an improper fraction is shown below
= (7 × 8 + 1) / 8
= (56 + 1) / 8
= 57 / 8
(iv)
The conversion of mixed fraction to an improper fraction is shown below
= (2 × 11 + 1) / 11
= (22 + 1) / 11
= 23 / 11
5. Change the following improper fractions to mixed fractions:
(i) 100 / 17
(ii) 81 / 11
(iii) – 209 / 7
(iv) – 113 / 15
Solution:
(i) 100 / 17
The conversion of an improper fraction into mixed fractions is shown below
100 / 17 =
(ii) 81 / 11
The conversion of an improper fraction into mixed fraction is shown below
81 / 11 =
(iii) -209 / 7
The conversion of an improper fraction into mixed fraction is shown below
-209 / 7 =
(iv) -113 / 15
The conversion of an improper fraction into mixed fraction is shown below
-113 / 15 =
6. Change the following groups of fractions to like fractions:
(i) 1 / 3, 2 / 5, 3 / 4, 1 / 6
(ii) 5 / 6, 7 / 8, 11 / 12, 3 / 10
(iii) 2 / 7, 7 / 8, 5 / 14, 9 / 16
Solution:
(i) 1 / 3, 2 / 5, 3 / 4, 1 / 6
The conversion of fractions to like fractions is shown below
LCM of the denominator 3, 5, 4, 6 = 60
= 2 × 3 × 1 × 5 × 2 × 1
= 60
1 / 3 = (1 × 20) / (3 × 20)
= 20 / 60
2 / 5 = (2 × 12) / (5 × 12)
= 24 / 60
3 / 4 = (3 × 15) / (4 × 15)
= 45 / 60
1 / 6 = (1 × 10) / (6 × 10)
= 10 / 60
Hence 1 / 3, 2 / 5, 3 / 4, 1 / 6 = 20 / 60, 24 / 60, 45 / 60, 10 / 60
(ii) 5 / 6, 7 / 8, 11 / 12, 3 / 10
The conversion of fractions to like fractions is shown below
LCM of the denominators 6, 8, 12, 10 = 120
= 2 × 2 × 3 × 1 × 2 × 1 × 5
= 120
5 / 6 = (5 × 20) / (6 × 20)
= 100 / 120
7 / 8 = (7 × 15) / (8 × 15)
= 105 / 120
11 / 12 = (11 × 10) / (12 × 10)
= 110 / 120
3 / 10 = (3 × 12) / (10 × 12)
= 36 / 120
Hence 5 / 6, 7 / 8, 11 / 12, 3 / 10 = 100 / 120, 105 / 120, 110 / 120, 36 / 120
(iii) 2 / 7, 7 / 8, 5 / 14, 9 / 16
LCM of the denominators 7, 8, 14, 16 = 112
= 2 × 7 × 4 × 1 × 1 × 1 × 2
= 112
2 / 7 = (2 × 16) / (7 × 16)
= 32 / 112
7 / 8 = (7 × 14) / (8 × 14)
= 98 / 112
5 / 14 = (5 × 8) / (14 × 8)
= 40 / 112
9 / 16 = (9 × 7) / (16 × 7)
= 63 / 112
Hence 2 / 7, 7 / 8, 5 / 14, 9 / 16 = 32 / 112, 98 / 112, 40 / 112, 63 / 112
Exercise 14(B)
1. Reduce the given fractions to their lowest terms:
(i) 8 / 10
(ii) 50 / 75
(iii) 18 / 81
(iv) 40 / 120
(v) 105 / 70
Solution:
(i) 8 / 10
The fraction 8 / 10 can be simplified as below
8 / 10 = (8 ÷ 2) / (10 ÷ 2)
= 4 / 5
Hence 4 / 5 is the simplified form of 8 / 10
(ii) 50 / 75
The fraction 50 / 75 can be simplified as below
50 / 75 = (50 ÷ 25) / (75 ÷ 25)
= 2 / 3
Hence 2 / 3 is the simplified form of 50 / 75
(iii) 18 / 81
The fraction 18 / 81 can be simplified as below
18 / 81 = (18 ÷ 9) / (81 ÷ 9)
= 2 / 9
Hence 2 / 9 is the simplified form of 18 / 81
(iv) 40 / 120
The fraction 40 / 120 can be simplified as below
40 / 120 = (40 ÷ 40) / (120 ÷ 40)
= 1 / 3
Hence 1 / 3 is the simplified form of 40 / 120
(v) 105 / 70
The fraction 105 / 70 can be simplified as below
105 / 70 = (105 ÷ 35) / (70 ÷ 35)
= 3 / 2
Hence 3 / 2 is the simplified form of 105 / 70
2. State, whether true or false?
(i) 2 / 5 = 10 / 15
(ii) 35 / 42 = 5 / 6
(iii) 5 / 4 = 4 / 5
(iv) 7 / 9 = 
(v) 9 / 7 = 
Solution:
(i) 2 / 5 = 10 / 15
The given expression can be solved as below
2 / 5 = (10 ÷ 5) / (15 ÷ 5)
2 / 5 ≠ 2 / 3
Hence false
(ii) 35 / 42 = 5 / 6
The given expression can be solved as below
(35 ÷ 7) / (42 ÷ 7) = 5 / 6
5 / 6 = 5 / 6
Hence true
(iii) 5 / 4 = 4 / 5
The given expression can be solved as below
5 / 4 ≠ 4 / 5
Hence false
(iv) 7 / 9 = 
The given expression can be solved as below
7 / 9 = (7 × 1 + 1) / 7
7 / 9 ≠ 8 / 7
Hence false
(v) 9 / 7 =
The given expression can be solved as below
9 / 7 = (7 × 1 + 1) / 7
9 / 7 ≠ 8 / 7
Hence false
3. Which fraction is greater?
(i) 3 / 5 or 2 / 3
(ii) 5 / 9 or 3 / 4
(iii) 11 / 14 or 26 / 35
Solution:
(i) 3 / 5 or 2 / 3
The given fractions can be simplified as follows
LCM of 5, 3 is 15
Hence 3 / 5 = (3 × 3) / (5 × 3)
= 9 / 15 and
2 / 3 = (2 × 5) / (3 × 5)
= 10 / 15
We know that
10 / 15 > 9 / 15 [Numerator is greater]
Thus, 2 / 3 > 3 / 5
Hence 2 / 3 is greater fraction
(ii) 5 / 9 or 3 / 4
The given expression can be simplified as follows
First convert the given expression into like fractions
So, 5 / 9 = (5 × 4) / (9 × 4)
= 20 / 36 and
3 / 4 = (3 × 9) / (4 × 9)
= 27 / 36
We know that
27 / 36 > 20 / 36 [Numerator is greater]
Thus 3 / 4 > 5 / 9
Hence 3 / 4 is greater fraction
(iii) 11 / 14 or 26 / 35
The given expression can be simplified as follows
First convert the given expression into like fractions
So, 11 / 14 = (11 × 5) / (14 × 5)
= 55 / 70 and
26 / 35 = (26 × 2) / (35 × 2)
= 52 / 70
We know that
55 / 70 > 52 / 70 [Numerator is greater]
Thus, 11 / 14 > 26 / 35
Hence 11 / 14 is greater fraction
4. Which fraction is smaller?
(i) 3 / 8 or 4 / 5
(ii) 8 / 15 or 4 / 7
(iii) 7 / 26 or 10 / 39
Solution:
(i) 3 / 8 or 4 / 5
The given expression can be simplified as follows
First convert the given expression into like fractions
So, 3 / 8 = (3 × 5) / (8 × 5)
= 15 / 40 and
4 / 5 = (4 × 8) / (5 × 8)
= 32 / 40
We know that
15 / 40 < 32 / 40 [Numerator is smaller]
Thus, 3 / 8 < 4 / 5
Hence 3 / 8 is the smaller fraction
(ii) 8 / 15 or 4 / 7
The given expression can be simplified as follows
First convert the given expression into like fractions
So, 8 / 15 = (8 × 7) / (15 × 7)
= 56 / 105 and
4 / 7 = (4 × 15) / (7 × 15)
= 60 / 105
We know that
56 / 105 < 60 / 105 [Numerator is smaller]
Thus, 8 / 15 < 4 / 7
Hence 8 / 15 is the smaller fraction
(iii) 7 / 26 or 10 / 39
The given expression can be simplified as follows
First convert the given expression into like fractions
So, 7 / 26 = (7 × 3) / (26 × 3)
= 21 / 78 and
10 / 39 = (10 × 2) / (39 × 2)
= 20 / 78
We know that
20 / 78 < 21 / 78 [Numerator is smaller]
Thus, 10 / 39 < 7 / 26
Hence 10 / 39 is the smaller fraction
5. Arrange the given fractions in descending order of magnitude:
(i) 5 / 16, 13 / 24, 7 / 8
(ii) 4 / 5, 7 / 15, 11 / 20, 3 / 4
(iii) 5 / 7, 3 / 8, 9 / 11
Solution:
(i) 5 / 16, 13 / 24, 7 / 8
The given expression can be simplified as follows
LCM of 16, 24, 8 = 2 × 2 × 2 × 2 × 3
= 48
Converting given expression into like fractions, we get
5 / 16 = (5 × 3) / (16 × 3)
= 15 / 48 and
13 / 24 = (13 × 2) / (24 × 2)
= 26 / 48 and
7 / 8 = (7 × 6) / (8 × 6)
= 42 / 48
Hence, fractions in descending order are 7 / 8, 13 / 24, 5 / 16
(ii) 4 / 5, 7 / 15, 11 / 20, 3 / 4
The given expression can be simplified as follows
LCM of 5, 15, 20, 4 = 4 × 5 × 3
= 60
Converting the given expression into like fractions, we get
4 / 5 = (4 ×12) / (5 × 12)
=48 / 60 and
7 / 15 = (7 × 4) / (15 × 4)
= 28 / 60 and
11 / 20 = (11 × 3) / (20 × 3)
= 33 / 60 and
3 / 4 = (3 × 15) / (4 × 15)
= 45 / 60
Hence, fractions in descending order are 4 / 5, 3 / 4, 11 / 20, 7 / 15
(iii) 5 / 7, 3 / 8, 9 / 11
The given expression can be simplified as follows
LCM of 5, 3, 9 = 3 × 3 × 5
= 45
Converting the given expression into like fractions, we get
5 / 7 = (5 × 9) / (7 × 9)
= 45 / 63 and
3 / 8 = (3 × 15) / (8 × 15)
= 45 / 120 and
9 / 11 = (9 × 5) / (11 × 5)
= 45 / 55
The fraction with the smallest denominator is the biggest fraction if the numerator is same
Hence, fractions in descending order are
45 / 55, 45 / 63, 45 / 120 i.e
9 / 11, 5 / 7, 3 / 8
6. Arrange the given fractions in ascending order of magnitude:
(i) 9 / 16, 7 / 12, 1 / 4
(ii) 5 / 6, 2 / 7, 8 / 9, 1 / 3
(iii) 2 / 3, 5 / 9, 5 / 6, 3 / 8
Solution:
(i) 9 / 16, 7 / 12, 1 / 4
The given fractions can be simplified as follows
LCM of 16, 12, 4 = 48
Converting the given expression into like fractions, we get
9 / 16 = (9 × 3) / (16 × 3)
= 27 / 48 and
7 / 12 = (7 × 4) / (12 × 4)
= 28 / 48 and
1 / 4 = (1 × 12) / (4 × 12)
= 12 / 48
Hence, fractions in ascending order are
12 / 48, 27 / 48, 28 / 48 i.e
1 / 4, 9 / 16, 7 / 12
(ii) 5 / 6, 2 / 7, 8 / 9, 1 / 3
The given fractions can be simplified as follows
LCM of 6, 7, 9, 3 = 3 × 3 × 2 × 7
= 126
Converting the given expression into like fractions, we get
5 / 6 = (5 × 21) / (6 × 21)
= 105 / 126 and
2 / 7 = (2 × 18) / (7 × 18)
= 36 / 126 and
8 / 9 = (8 × 14) / (9 × 14)
= 112 / 126 and
1 / 3 = (1 × 42) / (3 × 42)
= 42 / 126
Hence, fractions in ascending order are
36 / 126, 42 / 126, 105 / 126, 112 / 126 i.e
2 / 7, 1 / 3, 5 / 6, 8 / 9
(iii) 2 / 3, 5 / 9, 5 / 6, 3 / 8
The given fractions can be simplified as follows
LCM of 3, 9, 6, 8 = 72
Converting the given expressions into like fractions, we get
2 / 3 = (2 × 24) / (3 × 24)
= 48 / 72 and
5 / 9 = (5 × 8) / (9 × 8)
= 40 / 72 and
5 / 6 = (5 × 12) / (6 × 12)
= 60 / 72 and
3 / 8 = (3 × 9) / (8 × 9)
= 27 / 72
Hence, fractions in ascending order are
27 / 72, 40 / 72, 48 / 72, 60 / 72 i.e
3 / 8, 5 / 9, 2 / 3, 5 / 6
7. I bought one dozen bananas and ate five of them. What fraction of the total number of bananas was left?
Solution:
Given
Number of bananas bought = 1 dozen
We know there are 12 bananas in a dozen
Number of bananas eaten = 5
Number of bananas left = 12 – 5
= 7
Therefore, the required fraction is 7 / 12
8. Insert the symbol ‘=’ or ‘>’ or ‘<’ between each of the pairs of fractions, given below:
(i) 6 / 11 …. 5 / 9
(ii) 3 / 7 ….. 9 / 13
(iii) 56 / 64 …. 7 / 8
(iv) 5 / 12 …. 8 / 33
Solution:
(i) 6 / 11 …. 5 / 9
LCM of 11, 9 = 99
Converting the given expression into like fraction
We get
6 / 11 = (6 × 9) / (11 × 9)
= 54 / 99 and
5 / 9 = (5 × 11) / (9 × 11)
= 55 / 99
Therefore,
54 / 99 < 55 / 99 i.e
6 / 11 < 5 / 9
(ii) 3 / 7 ….. 9 / 13
LCM of 7, 13 = 91
Converting the given expression into like fraction
We get
3 / 7 = (3 × 13) / (7 × 13)
= 39 / 91 and
9 / 13 = (9 × 7) / (13 × 7)
= 63 / 91
Therefore,
39 / 91 < 63 / 91 i.e.
3 / 7 < 9 / 13
(iii) 56 / 64 …. 7 / 8
LCM of 64, 8 = 64
Converting the given expression into like fraction
We get
56 / 64 = (56 × 1) / (64 × 1)
= 56 / 64 and
7 / 8 = (7 × 8) / (8 × 8)
= 56 / 64
Therefore,
56 / 64 = 56 / 64 i.e.
56 / 64 = 7 / 8
(iv) 5 / 12 …. 8 / 33
LCM of 12, 33 = 132
Converting the given expression into like fractions
We get
5 / 12 = (5 × 11) / (12 × 11)
= 55 / 132 and
8 / 33 = (8 × 4) / (33 × 4)
= 32 / 132
55 / 132 > 32 / 132 i.e
5 / 12 > 8 / 33
9. Out of 50 identical articles, 36 are broken. Find the fraction of:
(i) The total number of articles and the articles broken.
(ii) The remaining articles and total number of articles.
Solution:
(i) Given
Total number of articles = 50
Number of articles broken = 36
Remaining articles = 50 – 36
= 14
The fraction of total number of articles and articles broken = 50 / 36
= 25 / 18
(ii) Given
Total number of articles = 50
Number of articles broken = 36
Remaining articles = 50 – 36
= 14
The fraction of remaining articles and total number of articles = 14 / 50
= 7 / 25
Exercise 14(C)
1. Add the following fractions:
(i) 
and 3 / 8
(ii) 2 / 5, 
and 7 / 10
(iii) 
, 
and 
(iv) 
, 
, and 
(v) 
, 11 / 18 and 
Solution:
(i)
and 3 / 8
The given fractions can be added as follows
7 / 4 + 3 / 8 = (7 × 2) / (4 × 2) + 3 / 8
= 14 / 8 + 3 / 8
= 17 / 8
=
Hence,
is the addition of given fractions
(ii) 2 / 5,
and 7 / 10
The given fractions can be added as follows
2 / 5 + 33 / 15 + 7 / 10 = (2 × 6) / (5 × 6) + (33 × 2) / (15 × 2) + (7 × 3) / (10 × 3)
= 12 / 30 + 66 / 30 + 21 / 30
= 99 / 30
= 33 / 10
=
Hence,
is the addition of given fractions
(iii)
,
and
The given fractions can be added as follows
15 / 8 + 3 / 2 + 7 / 4 = (15 × 1) / (8 × 1) + (3 × 4) / (2 × 4) + (7 × 2) / (4 × 2)
= 15 / 8 + 12 / 8 + 14 / 8
= 41 / 8
=
Hence,
is the addition of the given fractions
(iv)
,
and
The given fractions can be added as follows
15 / 4 + 13 / 6 + 13 / 8 = (15 × 6) / (4 × 6) + (13 × 4) / (6 × 4) + (13 × 3) / (8 × 3)
= 90 / 24 + 52 / 24 + 39 / 24
= 181 / 24
=
Hence,
is the addition of given fractions
(v)
, 11 / 18 and
The given fractions can be added as follows
26 / 9 + 11 / 18 + 23 / 6 = (26 × 2) / (9 × 2) + 11 / 18 + (23 × 3) / (6 × 3)
= 52 / 18 + 11 / 18 + 69 / 18
= 132 / 18
= 22 / 3
=
Hence,
is the addition of given fractions
2. Simplify:
(i) 
– 13 / 16
(ii) 
– 
(iii) 
+ 3 / 14 – 13 / 21
(iv) 
– 1 / 6 – 
(v) 6 + 3 / 10 – 
Solution:
(i)
– 13 / 16
The given expression can be simplified as below
23 / 12 – 13 / 16 = (23 × 4) / (12 × 4) – (13 × 3) / (16 × 3)
= (92 – 39) / 48
= 53 / 48
=
Hence, simplified form of the given expression is
(ii)
–
The given expression can be simplified as below
11 / 4 – 11 / 6 = (11 × 6) / (4 × 6) – (11 × 4) / (6 × 4)
= (66 – 44) / 24
= 22 / 24
= 11 / 12
Hence, simplified form of the given expression is 11 / 12
(iii)
+ 3 / 14 – 13 / 21
The given expression can be simplified as below
19 / 7 + 3 / 14 – 13 / 21 = (19 × 6) / (7 × 6) + (3 × 3) / (14 × 3) – (13 × 2) / (21 × 2)
= 114 / 42 + 9 / 42 – 26 / 42
= (114 + 9 – 26) / 42
= 97 / 42
=
Hence, simplified form of the given expression is
(iv)
– 1 / 6 –
The given expression can be simplified as below
23 / 6 – 1 / 6 – 13 / 12 = (23 × 2) / (6 × 2) – (1 × 2) / (6 × 2) – 13 / 12
= 46 / 12 – 2 / 12 – 13 / 12
= (46 – 2 – 13) / 12
= 31 / 12
=
Hence, simplified form of the given expression is
(v) 6 + 3 / 10 –
The given expression can be simplified as below
6 / 1 + 3 / 10 – 23 / 15 = (6 × 30) / (1 × 30) + (3 × 3) / (10 × 3) – (23 × 2) / (15 × 2)
= 180 / 30 + 9 / 30 – 46 / 30
= (180 + 9 – 46) / 30
= 143 / 30
=
Hence, simplified form of the given expression is
Exercise 14(D)
1. Simplify:
(i) 3 / 7 × 2 / 5
(ii) 4 / 9 × 3 / 5
(iii) 5 / 12 × 8
(iv) 7 / 6 of 3 / 14
(v) 
× 
Solution:
(i) 3 / 7 × 2 / 5
The given expression can be simplified as below
3 / 7 × 2 / 5 = (3 × 2) / (7 × 5)
= 6 / 35
Hence, the simplified form of the given expression is 6 / 35
(ii) 4 / 9 × 3 / 5
The given expression can be simplified as below
4 / 9 × 3 / 5 = (4 × 3) / (9 × 5)
= (4 × 1) / (3 × 5)
= 4 / 15
Hence, the simplified form of the given expression is 4 / 15
(iii) 5 / 12 × 8
The given expression can be simplified as below
5 / 12 × 8 / 1 = (5 × 8) / (12 × 1)
= (5 × 2) / (3 × 1)
= 10 / 3
=
Hence, the simplified form of the given expression is
(iv) 7 / 6 of 3 / 14
The given expression can be simplified as below
7 / 6 × 3 / 14 = (1 × 1) / (2 × 2)
= 1 / 4
Hence, the simplified form of the given expression is 1 / 4
(v)
×
The given expression can be simplified as below
×
= (27 × 27) / (8 × 7)
= 729 / 56
=
Hence, the simplified form of the given expression is
2. Simplify:
(i) 2 / 3 ÷ 
(ii) 
÷ 4 / 9
(iii) 1 ÷ 2 / 5
(iv) 4 / 9 ÷ 4 / 9
(v) 
÷ 
Solution:
(i) 2 / 3 ÷
The given expression can be simplified as below
2 / 3 ÷ 6 / 5 = (2 × 5) / (3 × 6)
= 5 / 9
Hence, the simplified form of the given expression is 5 / 9
(ii)
÷ 4 / 9
The given expression can be simplified as below
9 / 2 ÷ 4 / 9 = (9 × 9) / (2 × 4)
= 81 / 8
=
Hence, the simplified form of the given expression is
(iii) 1 ÷ 2 / 5
The given expression can be simplified as below
1 / 1 ÷ 2 / 5 = (1 × 5) / (1 × 2)
= 5 / 2
=
Hence, the simplified form of the given expression is
(iv) 4 / 9 ÷ 4 / 9
The given expression can be simplified as below
4 / 9 ÷ 4 / 9 = (4 × 9) / (9 × 4)
=1
Hence, the simplified form of the given expression is 1
(v)
÷
The given expression can be simplified as below
÷
= (7 × 4) / (3 × 7)
= 4 / 3
=
Hence, the simplified form of the given expression is
3. Simplify:
(i) 1 / 4 of 
÷ 3 / 5
(ii) 
× 1 / 2 ÷ 
(iii) 
× 0 × 
(iv) 3 / 4 × 
÷ 3 / 7 of 
(v) 
÷ 2 / 7 of 
× 2 / 3
Solution:
(i) 1 / 4 of
÷ 3 / 5
The given expression can be simplified as follows:
1 / 4 × 16 / 7 ÷ 3 / 5 = 4 / 7 ÷ 3 / 5
= (4 × 5) / (7 × 3)
= 20 / 21
Hence, 20 / 21 is the simplified form of the given expression
(ii) 
× 1 / 2 ÷
The given expression can be simplified as follows
× 1 / 2 ÷
= 5 / 4 × 1 / 2 × 3 / 4
= 5 / 8 × 3 / 4
= 15 / 32
Hence, 15 / 32 is the simplified form of the given expression
(iii)
× 0 × 
The given expression can be simplified as follows
× 0 × 
= (43 × 0 × 43) / (7 × 0 × 8)
= 0
Hence, 0 is the simplified form of the given expression
(iv) 3 / 4 ×
÷ 3 / 7 of
The given expression can be simplified as follows
3 / 4 ×
÷ 3 / 7 of
= 3 / 4 × 4 / 3 ÷ 9 / 8
∵ 3 / 7 of
= 3 / 7 × 21 / 8 = 9 / 8
= 3 / 4 × 4 / 3 × 8 / 9
= 8 / 9
Hence, 8 / 9 is the simplified form of the given expression
(v)
÷ 2 / 7 of
× 2 / 3
The given expression can be simplified as follows
[2 / 7 of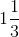
= 2 / 7 × 4 / 3 = 8 / 21]
We get
= 9 / 4 ÷ 8 / 21 × 2 / 3
= 9 / 4 × 21 / 8 × 2 / 3
= 63 / 16
=
Hence,
is the simplified form of the given expression
4. Simplify:
(i) 5 – (8 / 11 – 
)
(ii) 1 / 2 ÷ (7 / 8 – 3 / 5)
(iii) 
÷ (
+ 
)
(iv) (
–
) ÷ 1 / 2
(v) 4 / 7 ÷ (1 / 3 ×
)
Solution:
(i) 5 – (8 / 11 – 
)
The given expression can be simplified as below
5 – (8 / 11 –
) = 5 – (8 / 11 – 36 / 11)
= 5 – (8 – 36) / 11
= 5 – (-28 / 11)
On further calculation, we get
= 5 / 1 + 28 / 11
= 83 / 11
=
Hence,
is the simplified form of the given expression
(ii) 1 / 2 ÷ (7 / 8 – 3 / 5)
The given expression can be simplified as below
1 / 2 ÷ (7 / 8 – 3 / 5) = 1 / 2 ÷ (5 × 7 – 8 × 3) / 40
= 1 / 2 ÷ (35 – 24) / 40
= 1 / 2 ÷ (11 / 40)
= 1 / 2 × 40 / 11
We get
= 20 / 11
=
Hence,
is the simplified form of the given expression
(iii)
÷ (
+ 
)
The given expression can be simplified as below
÷ (
+ 
) = 7 / 3 ÷ (11 / 2 + 15 / 4)
= 7 / 3 ÷ (2 × 11 + 1 × 15) / 4
On further calculation, we get
= 7 / 3 ÷ (22 + 15) / 4
= 7 / 3 ÷ (37 / 4)
= 7 / 3 × 4 / 37
= 28 / 111
Hence, 28 / 111 is the simplified form of the given expression
(iv) (
–
) ÷ 1 / 2
The given expression can be simplified as below
(
–
) ÷ 1 / 2 = (31 / 8 – 18 / 5) ÷ 1 / 2
By taking LCM, we get
= [(31 × 5 – 18 × 8) / (8 × 5)] ÷ 1 / 2
= (155 – 144) / 40 ÷ 1 / 2
= (11 / 40) ÷ 1 / 2
By calculating further, we get
= 11 / 40 × 2 / 1
= 11 / 20
Hence, 11 / 20 is the simplified form of the given expression
(v) 4 / 7 ÷ (1 / 3 ×
)
The given expression can be simplified as below
4 / 7 ÷ (1 / 3 ×
) = 4 / 7 ÷ (1 / 3 × 14 / 5)
= 4 / 7 ÷ (14 / 15)
On further calculation, we get
= 4 / 7 × 15 / 14
= 2 / 7 × 15 / 7
= 30 / 49
Hence, 30 / 49 is the simplified form of the given expression
5. Simplify
(i) (1 / 2 + 1 / 3) ÷ (1 / 4 – 1 / 6)
(ii) (24 / 35 ÷ 6 / 7 + 5 / 9) × 3 / 4
(iii) 3 / 4 of 
– 2 / 3 of 
(iv) 7 / 30 of (1 / 3 + 7 / 15) ÷ (5 / 6 – 3 / 5)
(v) 
– 
× 
+ 
Solution:
(i) (1 / 2 + 1 / 3) ÷ (1 / 4 – 1 / 6)
The given expression can be simplified as follows
(1 / 2 + 1 / 3) ÷ (1 / 4 – 1 / 6) = [(3 + 2) / 6] ÷ [(3 – 2) / 12]
On further calculation, we get
= (5 / 6) ÷ (1 / 12)
= 5 / 6 × 12 / 1
= 5 × 2
= 10
Hence, the simplified form of the given expression is 10
(ii) (24 / 35 ÷ 6 / 7 + 5 / 9) × 3 / 4
The given expression can be simplified as follows
(24 / 35 ÷ 6 / 7 + 5 / 9) × 3 / 4 = (24 / 35 × 7 / 6 + 5 / 9) × 3 / 4
= (4 / 5 + 5 / 9) × 3 / 4
By taking LCM, we get
= [(36 + 25) / 45] × 3 / 4
= (61 / 45) × 3 / 4
We get
= 61 / 60
=
Hence, the simplified form of the given expression is
(iii) 3 / 4 of
– 2 / 3 of
The given expression can be simplified as below
3 / 4 of
– 2 / 3 of
= 3 / 4 of 49 / 8 – 2 / 3 of 9 / 4
= 3 / 4 × 49 / 8 – 2 / 3 of 9 / 4
= 147 / 32 – 2 / 3 × 9 / 4
We get
= 147 / 32 – 3 / 2
On taking LCM, we get
= [(147 – 48)] / 32
= 99 / 32
=
Hence, the simplified form of the given expression is
(iv) 7 / 30 of (1 / 3 + 7 / 15) ÷ (5 / 6 – 3 / 5)
The given expression can be simplified as below
7 / 30 of (1 / 3 + 7 / 15) ÷ (5 / 6 – 3 / 5) = 7 / 30 of [(5 + 7) / 15] ÷ [(25 – 18) / 30]
We get
= 7 / 30 of (4 / 5) ÷ (7 / 30)
= 7 / 30 × 4 / 5 × 30 / 7
= 4 / 5
Hence, the simplified form of the given expression is 4 / 5
(v)
– 
× 
+ 
The given expression can be simplified as below
–
×
+
= 5 / 2 – 7 / 2 × 7 / 4 + 5 / 2
= 5 / 2 – 49 / 8 + 5 / 2
= 5 / 2 + 5 / 2 – 49 / 8
By taking LCM, we get
= (20 + 20 – 49) / 8
= (40 – 49) / 8
= – 9 / 8
= –
Hence, –
is the simplified form of the given expression
Exercise 14(e)
1. From a rope of 
m long, 
m is cut off. Find the length of the remaining rope
Solution:
Given
Length of the rope =
m
Length of cut off rope =
m
Remaining rope =
–
We get
= 21 / 2 – 37 / 8
By taking LCM, we get
= (84 – 37) / 8
= 47 / 8 m
=
Hence, the length of the remaining rope is
m
2. A piece of cloth is 5 metre long. After washing, it shrinks by 1 / 25 of its length. What is the length of the cloth after washing?
Solution:
Given
Length of piece of cloth = 5 metre
After washing, it shrinks by = 1 / 25 of its length
Hence, the shrinked cloth can be calculated as below
Shrinked cloth = 1 / 25 of 5 m
= 1 / 5 m
Hence, length of cloth after washing can be calculated as below
Length of cloth after washing = 5 – 1 / 5
By taking LCM, we get
= (25 – 1) / 5
= 24 / 5
=
m
Hence the length of cloth after washing is
m
3. I bought wheat worth Rs 
, rice worth Rs 
and vegetables worth Rs 
. If I gave a hundred-rupee note to the shopkeeper; how much did he return to me
Solution:
Given
Wheat = Rs
Rice = Rs
Vegetables = Rs
Hence, total amount used to purchase the goods can be calculated as below
Total amount of goods = Rs (
+
+
)
We get
= 25 / 2 + 103 / 4 + 41 / 4
= Rs 194 / 4
Hence, money returned by shopkeeper can be calculated as below
Money returned = Rs (100 – 194 / 4)
By taking LCM, we get
= Rs (400 – 194) / 4
= Rs 103 / 2
= Rs
Hence, money returned by the shopkeeper is Rs
4. Out of 500 oranges in a box, 3 / 25 are rotten and 1 / 5 are kept for some guests. How many oranges are left in the box?
Solution:
Given
Number of oranges in a box = 500
Rotten oranges out of 500 = 3 / 25
Oranges for guests out of 500 = 1 / 5
Rotten oranges = 3 / 25 of 500
We get,
= 3 / 25 × 500
= 60
Oranges for guests = 1 / 5 of 500
We get,
= 1 / 5 × 500
= 100
Oranges left in box = 500 – 60 – 100
= 340
Hence, 340 oranges are left in the box
5. An ornament piece is made of gold and copper. Its total weight is 96 g. If 1 / 12 of the ornament is copper, find the weight of gold in it.
Solution:
Given
Weight of an ornament = 96 g
Weight of copper = 1 / 12 of 96 g
Weight of copper = 1 / 12 × 96
We get,
= 8 g
Weight of gold = 96 – 8
= 88 g
Hence, the weight of gold in ornament is 88 g
6. A girl did half of some work on Monday and one-third of it on Tuesday. How much will she have to do on Wednesday in order to complete the work?
Solution:
Given
Half of work is done on Monday and one-third on Tuesday by a girl
Let total work done by a girl is 1
Work done on Monday = 1 / 2
Work done on Tuesday = 1 / 3
Hence, remaining work done on Wednesday to complete the work is calculated as below
Remaining work done = 1 – [(1 / 2 + 1 / 3)]
Taking LCM, we get
= 1 – [(3 + 2) / 6]
= 1 – 5 / 6
= (6 – 5) / 6
= 1 / 6
Hence, work done by a girl on Wednesday to complete is 1 / 6
7. A man spends 3 / 8 of his money and 8 still has Rs 720 left with him. How much money did he have at first?
Solution:
Given
Man spends 3 / 8 of his money
Let us assume a man has Rs 1
Amount spent = 3 / 8 of 1
We get,
= Rs 3 / 8
Amount left = 1 – 3 / 8
We get,
= (8 – 3) / 8
= Rs 5 / 8
Since 5 / 8 of his total money = Rs 720
∴ Total money = Rs (720 × 8) / 5
= Rs 5760 / 5
= Rs 1152
Hence, total money a man has is Rs 1152
8. In a school, 4 / 5 of the students are boys, and the number of girls is 100. Find the number of boys
Solution:
Given
Total number of girls = 100
Number of boys = 4 / 5
Let us assume the total number of boys and girls be x
Total number of boys = 4 / 5 of x
We get,
= 4x / 5
According to question, total strength of school can be calculated as below
x – (4x/5) = 100
(5x – 4x)/5 = 100
x = 500
Number of boys = Total strength – Girls
= 500 – 400
= 400
Hence number of boys are 400
9. After finishing 3 / 4 of my journey, I find that 12 km of my journey is covered. How much distance is still left to be covered?
Solution:
Let x km be the total journey
Given that total distance covered = 3 / 4 of the journey is 12 km
According to the question, the distance covered can be calculated as below
3 / 4 of x = 12 km
x = 4 / 3 × 12
x = 4 × 4
x = 16 km
Remaining distance = 16 – 12
= 4 km
Hence, 4 km of distance is left to be covered
10. When Ajit travelled 15 km, he found that one-fourth of his journey was still left. What was the full length of the journey?
Solution:
Let the total journey = x km
Given total distance covered = 15 km
Journey left = 1 / 4 of x
Hence, according to the question, the total distance of journey can be calculated as below
1 / 4 of x = x – 15
x – x / 4 = 15
By calculating further, we get
(4x – x) / 4 = 15
3x / 4 = 15
3x = 60
x = 60 / 3
x = 20
Hence, the full length of the journey is 20 km
11. In a particular month, a man earns Rs 7, 200. Out of this income, he spends 3 / 10 on food, 1 / 4 on house rent, 1 / 10 on insurance and 2 / 25 on holidays. How much did he save in that month?
Solution:
Given
Money earned by a man in a particular month = Rs 7200
Amount spend on food, house rent, insurance and holidays by him are 3 / 10, 1 / 4, 1 / 10 and 2 / 25 respectively
Amount spend on food = 3 / 10 of 7200
= 3 / 10 × 7200
= 3 × 720
= Rs 2160
Amount spend on house rent = 1 / 4 of 7200
= 1 / 4 × 7200
= Rs 1800
Amount spend on insurance = 1 / 10 of 7200
= 1 / 10 × 7200
= Rs 720
Amount spend on holidays = 2 / 25 of 7200
= 2 / 25 × 7200
= Rs 576
Total amount spend = Rs (2160 + 1800 + 720 + 576)
= Rs 5256
Amount saved by man = 7200 – 5256
= Rs 1944
Hence, amount saved by a man in a month is Rs 1944
Comments