Conjugates of Complex Numbers

A conjugate of a complex number is another complex number that has the same real part as the original complex number, and the imaginary part has the same magnitude but opposite sign. If we multiply a complex number with its conjugate, we get a real number. The conjugates of complex numbers give the mirror image of the complex number about the real axis in the argand plane. In this article, we will learn the conjugates of complex numbers and their properties, along with solved examples.

A number of the form z = x + iy, where x and y are real numbers, is called a complex number. Here, x is called the real part, and y is called the imaginary part. The imaginary number ‘i’ is the square root of -1. Consider a complex number z = a + ib. The conjugate of this complex number is denoted by

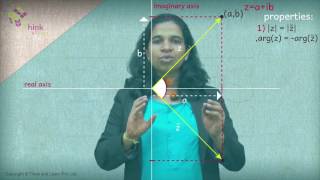
Here, the conjugate (a – ib) is the reflection of the complex number a + ib about the X-axis (real-axis) in the argand plane. In polar form, the complex conjugate of the complex number re^iθ is re^-iθ. To rationalise the complex number, the complex conjugate of a complex number is used. Consider the complex number 3 – 2i. Here, the complex conjugate is 3 + 2i. The following figure will give you a clear idea of the conjugate of a complex number.

Properties of Conjugates of Complex Numbers

1. \(\begin{array}{l}\text{The modulus of z is equal to the modulus of }\ \bar{z}.\end{array} \)
   \(\begin{array}{l}|z| = \left |\bar{z} \right |\end{array} \)
   \(\begin{array}{l}arg\ z = -arg(\bar{z})\end{array} \)
2. If z is purely real, then
   \(\begin{array}{l}z =\bar{z}\end{array} \)
3. If z is purely imaginary, then
   \(\begin{array}{l}z =-\bar{z}\end{array} \)
4. The complex conjugate of the product of two complex numbers is equal to the product of the complex conjugates of the two complex numbers.
   
   \(\begin{array}{l}\overline{z_{1}z_{2}}=\bar{z_{1}} .\bar{z_{2}}\end{array} \)
5. The complex conjugate of the quotient of two complex numbers is equal to the quotient of the complex conjugates of the two complex numbers.
   
   \(\begin{array}{l}\overline{\left ( \frac{z_{1}}{z_{2}} \right )}= \frac{\overline{z_{1}}}{\overline{z_{2}}};\ z_2 \neq 0.\end{array} \)
6. If we add a complex number and its conjugate, then the sum is equal to 2Re(z).
   
   \(\begin{array}{l}z+\bar{z}=2Re(z)\end{array} \)
7. \(\begin{array}{l}z\bar{z}=\left | z \right |^{2}\end{array} \)
8. \(\begin{array}{l}z-\bar{z}=2Im(z)\end{array} \)
9. \(\begin{array}{l}\overline{\overline{z}}= z\end{array} \)

Also, Read

Complex Number Solved Examples

Geometry of Complex Numbers

Solved Examples

Example 1:

If z = 2/(1-i), then the conjugate of z is

1) (1-i)

2) 1+i

3) 2/(1+i)

4) None of these

Solution:

If z = x + iy, then the conjugate of z is x – iy.

Z = 2/(1 – i)

= 2(1 + i)/(1 – i)(1 + i)

= 2(1 + i)/2

= (1 + i)

Hence, option (1) is the answer.

Example 2:

1) 3

2) 8

3) 10

4) None of these

Solution:

Given

Suppose, z = x+iy

Substituting the above values in (i), we get,

(3 + i)2x – (2 + i)2iy + 14i = 0

6x + 2ix – 4iy + 2y + 14i = 0

(6x + 2y) + (2x – 4y + 14)i = 0

Comparing the real part, we get

6x + 2y = 0

6x = -2y

y = 6x/-2

y = -3x

Comparing the imaginary part, we get

2x – 4y + 14 = 0

Put y = -3x in above equation

2x + 12x + 14 = 0

14x = -14

x = -1

So, y = 3

Now, z = -1 + 3i

= 1 + 9

= 10

Hence, option (3) is the answer.

Related Video