JEE Main 2020 Maths paper for September 4 Shift 1 with solutions are available on this page. Students can view or download the question paper and analyze the different aspects of the JEE Main exam paper including exam pattern, weightage of marks, difficulty level and more. Students can also practice solving the question and the solutions which have been prepared by our experts will help them understand the answers more clearly. These solutions are available in PDF format and can be accessed for free.
JEE Main 2020 Question Papers
September 4 Shift 1 – Maths
Download PDF 
September 4 Shift 1 – Maths
Question 1.Let y = y(x) be the solution of the differential equation, xy’-y = x2(xcosx+sinx),x > 0. If y(π) = π, then y’’(π/2)+y(π/2) is equal to:
a) 2+(π/2)+(π2/4)
b) 2+(π/2)
c) 1+(π/2)
d) 1+(π/2)+ (π2/4)
xy’-y = x2(x cosx + sinx) x > 0, y(π) =π
y’-(1/x)y = x(x cosx+sin x)
I.F =
\(\begin{array}{l}e^{-\int\frac{1}{x}dx }\end{array} \)
= e– ln x
= 1/x
y(1/x) = ∫(1/x)x(x cos x+sin x) dx
(y/x) = ∫(x cos x+ sin x) dx
(y/x) = ∫ (d/dx)(x sin x) dx
(y/x) = x sin x+C
y = x2 sin x+Cx
x = π, y = π
π = πC
C = 1
y = x2 sin x+x
y(π/2) = (π2/4)+(π/2)
y’ = 2x sinx+x2cosx+1
y’’ = 2sinx+2xcosx+2x cosx-x2sinx
y’’(π/2) = 2-(π2/4)
y(π/2)+ y’’(π/2) = 2+π/2
Answer:(b)
Question 2. The value of \(\begin{array}{l}\sum_{r=0}^{20} \: ^{50-r}C_{6}\end{array} \)
is equal to:
a) 51C7–30C7
b) 51C7+30C7
c) 50C7–30C7
d) 50C6–30C6
\(\begin{array}{l}\sum_{r=0}^{20} \: ^{50-r}C_{6}\end{array} \)
= 50C6+49C6+48C6+…+31C6+30C6
Add and subtract 30C7
Using nCr+ nCr-1 = n+1Cr
30C6+30C7 = 31C7
31C6+31C7 = 32C7
Similarly solving
51C7–30C7
Answer: (a)
Question 3. Let [t] denote the greatest integer ≤ t. Then the equation in x, [x]2+2[x+2]-7 = 0 has:
a) exactly four integral solutions.
b) infinitely many solutions.
c) no integral solution.
d) exactly two solutions.
[x]2+2[x+2]-7 = 0
[x]2 +2[x]-3 = 0
let [x] = y
y2+3y-y -3 = 0
(y -1)(y+3) = 0
[x] = 1 or [x] = -3
x ∈ [1,2) or x ∈ [-3,-2)
Answer: (b)
Question 4. Let P(3, 3) be a point on the hyperbola, (x2/a2)-(y2/b2) = 1. If the normal to it at P intersects the x-axis at (9, 0) and e is its eccentricity, then the ordered pair (a2, e2) is equal to:
a) (9, 3)
b) (9/2, 2)
c) (9/2, 3)
d) (3/2, 2)
(x2/a2)-(y2/b2) = 1
Point P(3, 3) on hyperbola.
(9/a2)-(9/b2) = 1 ..(i)
Equation of normal (a2x/3)+(b2y)/3 = a2e2
At x axis y = 0
a2x/3 = a2e2
x = 3e2 = 9
3e2 = 9
e2 = 3
e = √3
e2 = 1+b2/a2 = 3
b2 = 2a2 ..(ii)
Put in equation 1
(9/a2)-(9/2a2) = 1
(9/2a2) = 1
a2 = 9/2
(a2, e2) = (9/2,3)
Answer: (c)
Question 5. Let (x2/a2)+(y2/b2) = 1 (a>b) be a given ellipse, length of whose latus rectum is 10. If its eccentricity is the maximum value of the function, Φ(t) = (5/12)+t-t2, then a2+b2 is equal to:
a) 135
b) 116
c) 126
d) 145
L.R = 2b2/a = 10 ..(i)
Φ(t) = (5/12)-(t-1/2)2+(1/4)
= (8/12)-(t-1/2)2
Φ(t)max = 2/3 = e
e2 = 1-(b2/a2)
= 4/9
b2/a2 = 5/9
From (i)
b2/a.a = 5/9
5/a = 5/9
a = 9
b2 = 45
a2+b2 = 81+45 = 126
Answer: (c)
Question 6. Let \(\begin{array}{l}f(x) = \int \frac{\sqrt{x}}{(1+x)^{2}}dx\end{array} \)
, x≥0. Then f(3)-f(1) is equal to:
a) (-π/6)+(1/2)+(√3/4)
b) (π/6)+(1/2)-(√3/4)
c) (-π/12)+(1/2)+(√3/4)
d) (π/12)+(1/2)-(√3/4)
\(\begin{array}{l}f(x) = \int \frac{\sqrt{x}}{(1+x)^{2}}dx\end{array} \)
Substituting x = tan2t
dx = 2tan t sec2t dt
f(x) =
\(\begin{array}{l}\int \frac{\tan t. 2\tan t\sec ^{2}t}{\sec ^{4}t}dt\end{array} \)
f(x) = 2∫sin2t dt
x = 3 t = π/3
x = 1 t = π/4
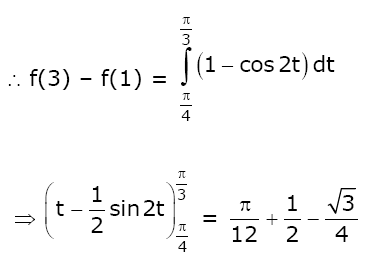
Answer: (d)
Question 7. If 1+(1-22×1)+(1-42×3)+(1-62×5)+……+(1-202×19) = α – 220β, then an ordered pair (α, β) is equal to:
a) (10,97)
b) (11,103)
c) (11,97)
d) (10,103)
Tn = 1-(2n)2(2n-1)
= 1-4n2(2n-1)
= 1-8n3+4n2
Sn =
\(\begin{array}{l}\sum_{n=1}^{10}T_{n}\end{array} \)
= n-∑8n3+∑4n2
= n-8×(n2(n+1)2/4)+4n(n+1)(2n+1)/6
S10 = 10-2×100×121 +(2/3)×10×11×21
= 10-24200+1540
= 10-22660
Sum of series = 11-220×103
= α – 220β
α = 11
β = 103
Answer: (b)
Question 8. The integral \(\begin{array}{l}\int \left ( \frac{x}{x\sin x+\cos x} \right )^{2}dx\end{array} \)
is equal to: (where C is a constant of integration)
a) tan x-(x sec x/(x sin x+cos x))+C
b) sec x-(x tan x/(x sin x+cos x))+C
c) sec x+(x tan x/(x sin x+cos x))+C
d) tan x+(x sec x/(x sin x+cos x))+C
\(\begin{array}{l}\int \left ( \frac{x}{x\sin x+\cos x} \right )^{2}dx\end{array} \)
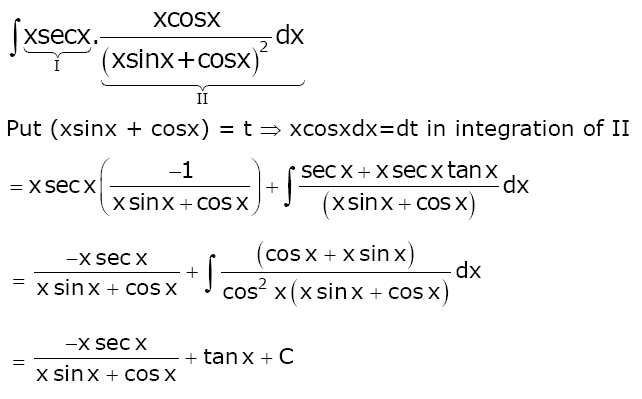
= tan x-(x sec x/(x sin x+cos x))+C
Answer: (a)
Question 9. Let f(x)= |x-2| and g(x) = f(f(x)) ,x∈0,4]. Then \(\begin{array}{l}\int_{0}^{3}(g(x)-f(x))dx\end{array} \)
is equal to:
a) 1/2
b) 0
c) 1
d) 3/2
f(x) = |x-2| =
\(\begin{array}{l}\left\{\begin{matrix} x-2, & x\geq 2\\ 2-x, & x< 2 \end{matrix}\right.\end{array} \)
g(x) = ||x-2|-2| =
\(\begin{array}{l}\left\{\begin{matrix} \left | x-4 \right |, & x\geq 2\\ \left | x \right |, & x< 2 \end{matrix}\right.\end{array} \)
=
\(\begin{array}{l}\left\{\begin{matrix} 4-x, & x\in [2,4)\\ x-4 ,&x\geq 4 \\ x, & x\in [0,2) \end{matrix}\right.\end{array} \)
\(\begin{array}{l}\int_{0}^{3}(g(x)-f(x))dx\end{array} \)
=
\(\begin{array}{l}\int_{0}^{3}g(x)dx-\int_{0}^{3}f(x)dx\end{array} \)
= [(1/2)×2×2+1+(1/2)×1×1]-[(1/2)×2×2+(1/2)×1×1)]
= (7/2)-(5/2)
= 1

Answer: (c)
Question 10. Let x0 be the point of local maxima of f(x) = \(\begin{array}{l}\vec{a}.(\vec{b}\times \vec{c})\end{array} \)
where \(\begin{array}{l}\vec{a}= x\hat{i}-2\hat{j}+3\hat{k}\end{array} \)
, \(\begin{array}{l}\vec{b}= -2\hat{i}+x\hat{j}-\hat{k}\end{array} \)
and \(\begin{array}{l}\vec{c}= 7\hat{i}-2\hat{j}+x\hat{k}\end{array} \)
. Then the value of \(\begin{array}{l}\vec{a}.\vec{b}+\vec{b}.\vec{c}+\vec{c}.\vec{a}\end{array} \)
at x = x0 is:
a) -22
b) -4
c) -30
d) 14
\(\begin{array}{l}\vec{a}.(\vec{b}\times \vec{c})\end{array} \)
=
\(\begin{array}{l}\begin{vmatrix} x & -2 & 3\\ -2 & x & -1\\ 7 & -2 & x \end{vmatrix}\end{array} \)
= x(x2-2)+2(-2x+7)+ 3(4-7x)
= x3-2x- 4x+14+12-21x
f(x) = x3– 27x+26
f’(x) = 3x2-27 = 0
x = 3
f’’(x) = 6x
at x = 3, f” (3) = 6×3= 18 > 0
at x = -3, f” (-3) = 6×3 = -18 < 0
Max at x0 = -3
\(\begin{array}{l}\vec{a}= (-3,-2,3)\end{array} \)
, \(\begin{array}{l}\vec{b}= (-2,-3,-1)\end{array} \)
, \(\begin{array}{l}\vec{c}= (7,-2,-3)\end{array} \)
So
\(\begin{array}{l}\vec{a}.\vec{b}+\vec{b}.\vec{c}+\vec{c}.\vec{a}\end{array} \)
= 6+6-3-14+6+3-21+4-9
= 25-47
= -22
Answer: (a)
Question 11.A triangle ABC lying in the first quadrant has two vertices as A(1,2) and B(3,1). If BAC = 900 and ar(ΔABC) = 5√5 s units, then the abscissa of the vertex C is:
a) 1+√5
b) 1+2√ 5
c) 2√5-1
d) 2+√5

AB = √(4+1) = √5
(1/2)×√5×x = 5√5
x = 10
mAB = -1/2
mAC = 2 = tanθ
Since sinθ = 2/√5
cosθ = 1/√5
by parametric co-ordinates
a = 1+ xcosθ = 1+10×1/√5
= 1+2√5
Answer: (b)
Question 12.Let f be a twice differentiable function on (1,6). If f(2) = 8, f’(2) = 5, f’(x) ≥1 and f’’(x) ≥4, for all x ∈ (1,6), then:
a) f(5)+f’(5) ≥28
b) f’(5)+f’’(5) ≤20
c) f(5) ≤10
d) f(5)+f’(5) ≤26
f(2) = 8, f’(2) = 5, f’(x) ≥1 and f’’(x) ≥4,
x∈(1,6)
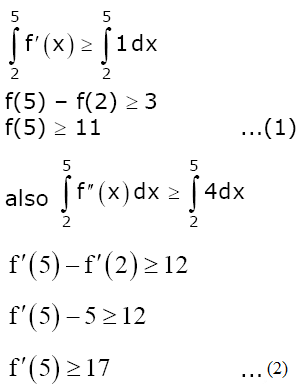
adding (1) and (2) we get,
f(5)+f’(5) ≥28
Answer: (a)
Question 13.Let α and β be the roots of x2-3x+p = 0 and 1/γ and 1/δ be the roots of x2-6x+q = 0. If α, β, γ, δ form a geometric progression. Then ratio (2q+p): (2q-p) is:
a) 33 :31
b) 9 : 7
c) 3 : 1
d) 5 : 3
Roots of x2-3x+p = 0 are α and β.
The roots of x2-6x+q = 0 are γ and δ.
α + β = 3
γ + δ = 6
α = a , β = ar, γ = ar2, δ = ar3
a(1+r) = 3 …(i)
ar2(1+r) = 6 …(ii)
Divide (ii) by (i)
r2 = 2
α.β = p = a2r
γ.δ = q = a2r5
(2q+p)/(2q-p) = (2r4+1)/( 2r4-1)
= (2×22+1)/( 2×22-1) = 9/7
Answer: (b)
Question 14. Let u = (2z+i)/(z-ki), z = x+iy and k>0. If the curve represented by Re(u) +Im(u) =1 intersects the y-axis at the points P and Q where PQ =5, then the value of k is:
a) 4
b) 1/2
c) 2
d) 3/2
u = (2z+i)/(z-ki)
z = x+iy

Re(u)+Img(u) = 1
2x2+(2y+1)(y -k )+x+2xk = x2 + (y-k)2
at y – axis, x = 0
(2y +1)(y- k) = (y- k )2
2y2 +y- 2yk- k = y2+k2-2yk
Roots of y2+y-(k +k2) = 0 are y1 and y2
Diff. of roots = 5
√(1+4k+4k2) = 5
4k2+4k = 24
k2+k-6 = 0
(k +3)(k-2) = 0
k = 2
Answer: (c)
Question 15. If A = \(\begin{array}{l}\begin{bmatrix} \cos \theta & i\sin \theta \\ i\sin \theta & \cos \theta \end{bmatrix}\end{array} \)
, (θ = π/24) and A5 = \(\begin{array}{l}\begin{bmatrix} a & b\\ c& d \end{bmatrix}\end{array} \)
, where i = √-1, then which one of the following is not true?
a) a2-d2 = 0
b) a2-c2 = 1
c) 0 ≤a2+b2 ≤1
d) a2-b2 = 1/2
A =
\(\begin{array}{l}\begin{bmatrix} \cos \theta & i\sin \theta \\ i\sin \theta & \cos \theta \end{bmatrix}\end{array} \)
A2 =
\(\begin{array}{l}\begin{bmatrix} \cos \theta & i\sin \theta \\ i\sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} \cos \theta & i\sin \theta \\ i\sin \theta & \cos \theta \end{bmatrix}\end{array} \)
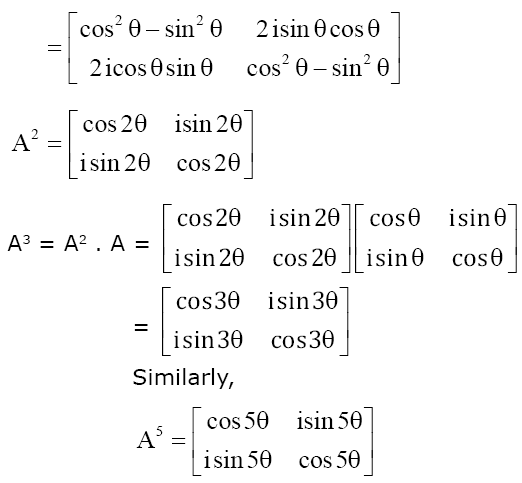
a = d = cos (5θ)
b = c = i sin (5θ)
a2-b2 = cos25θ + sin25θ
= 1
Answer: (d)
Question 16. The mean and variance of 8 observations are 10 and 13.5, respectively. If 6 of these observations are 5, 7, 10, 12, 14, 15, then the absolute difference of the remaining two observations is:
a) 3
b) 9
c) 7
d) 5
(5+7+10+12+14+15+x+y)/8 = 10
x+y = 17 ..(i)
Variance = (52+72+102+122+142+152+x2+y2)/8 -100 = 13.5
(739+x2+y2)/8 – 100 = 13.5
x2+y2 = 169 ..(ii)
∴ x = 12, y = 5
|x-y| = 7
Answer: (c)
Question 17. A survey shows that 63% of the people in a city read newspaper A whereas 76% read newspaper B. If x% of the people read both the newspapers, then a possible value of x can be:
a) 37
b) 29
c) 65
d) 55
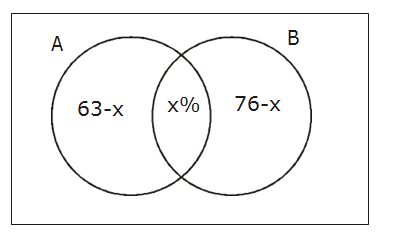
n(B) ≤n(A∪B) ≤n(U)
76 ≤76+63-x ≤100
-63 ≤-x ≤-39
63 ≥x ≥ 39
Answer (d)
Question 18.Given the following two statements
(S1): (q˅p)→(p ↔ ~q) is a tautology.
(S2): ~q ˄ (~p ↔ q) is a fallacy. Then:
a) only (S1) is correct.
b) both (S1) and (S2) are correct.
c) only (S2) is correct
d) both (S1) and (S2) are not correct.

Answer (d)
Question 19. Two vertical poles AB = 15 m and CD = 10 m are standing apart on a horizontal ground with points A and C on the ground. If P is the point of intersection of BC and AD, then the height of P (in m) above the line AC is:
a) 5
b) 20/3
c) 10/3
d) 6
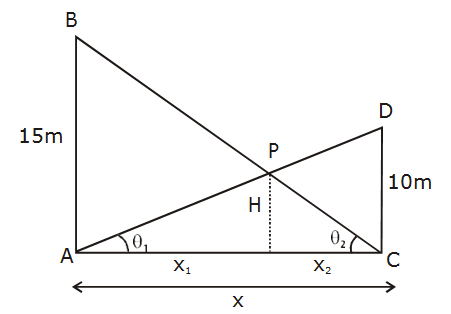
Using similar triangle concept
tan θ1 = 10/x = H/x1
x1 = Hx/10
tan θ2 = 15/x = H/x2
x2 = Hx/15
Since x1+x2 = x
(Hx/10)+( Hx/15) = x
15H+10H = 150
H = 150/25 = 6 m
Answer: (d)
Question 20. If (a+√2b cos x)( a-√2b cos y) = a2-b2, where a>b>0, then dy/dx at (π/4, π/4) is:
a) (a+b)/(a-b)
b) (a-2b)/(a+2b)
c) (a-b)/(a+b)
d) (2a+b)/(2a-b)
(a+√2b cos x)( a-√2b cos y) = a2-b2
Differentiating both sides w.r.t.y
-√2b sin x (dx/dy)(a-√2b cos y)+ (a+√2b cos x)(√2b sin y) = 0
x = y = π/4
-b(dx/dy) (a-b)+(a+b)b = 0
dx/dy = (a+b)/(a-b)
Answer: (a)
Question 21. Suppose a differentiable function f(x) satisfies the identity f(x+y) = f(x)+f(y)+xy2+x2y,for all real x and y. If \(\begin{array}{l}\lim_{x\to0}\frac{f(x)}{x}=1\end{array} \)
then f’(3) is equal to:
f(x+y) = f(x)+f(y)+xy2+x2y
x = y = 0
f(0) = 2f(0)
f(0) = 0
Now,

f’(x) = 1+0+x2
f’(x) = 1+x2
f’(3) = 10
Answer: (10)
Question 22.If the equation of a plane P, passing through the intersection of the planes, x+4y-z+7 = 0 and 3x+y+5z = 8 is ax+by+6z = 15 for some a, b∈R, then the distance of the point (3,2,-1) from the plane P is ….. units.
p1+λp2 = 0
(x +4y-z+7)+λ(3x+y+5z-8) = ax+by+6z-15
(1+3λ)/a = (4+λ)/b = (-1+5λ)/6 = (7-8λ)/-15
∴ 15-75λ = 42-48λ
-27 = 27λ
= -1
∴ plane is -2x+3y-6z+15 = 0
d = |-6+6+6+15)/√(4+9+36)|
= 3 units
Answer: (3)
Question 23. If the system of equations
x-2y+3z = 9
2x+y+z = b
x-7y+az = 24, has infinitely many solutions, then a-b is equal to:
D = 0
\(\begin{array}{l}\begin{vmatrix} 1 & -2& 3\\ 2 & 1 & 1\\ 1& -7 & a \end{vmatrix}\end{array} \)
= 0
1(a +7)+2(2a -1)+3(-14-1) = 0
a+7+4a-2-45 = 0
5a = 40
a = 8
D1 =
\(\begin{array}{l}\begin{vmatrix} 9 & -2& 3\\ b & 1 & 1\\ 24& -7 & 8 \end{vmatrix} = 0\end{array} \)
9(8+7)+2(8b-24)+3(-7b-24) = 0
135+16b-48-21b-72 = 0
15 = 5b
b = 3
Hence a – b = 8-3 = 5
Answer: (5)
Question 24.Let (2x2+3x+4)10 = \(\begin{array}{l}\sum_{r =0}^{20}a_{r}x^{r}\end{array} \)
. Then a7/a13 is equal to:
Given (2x2+3x+4)10 =
\(\begin{array}{l}\sum_{r =0}^{20}a_{r}x^{r}\end{array} \)
Replace x by 2/x in above identity:
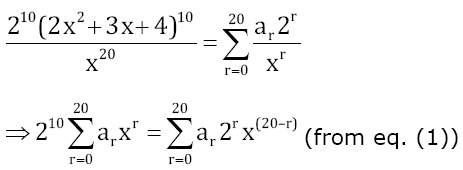
Now, comparing coefficient of x7 from both sides
(take r = 7 in L.H.S. and r = 13 in R.H.S)
210a7 = a13213
a7/a13 = 23 = 8
Answer: (8)
Question 25.The probability of a man hitting a target is 1/10. The least number of shots required, so that the probability of his hitting the target at least once is greater than 1/4 is:
Probability of hitting, P(H) = 1/10
probability of missing, P(M) = 9/10
We have, 1-(probability of all shots result in failure ) >1/4
= 1-P(M)n > 1/4
= 1-(9/10)n > 1/4
(9/10)n <3/4
n≥3
Answer (3)
Video Lessons – Maths
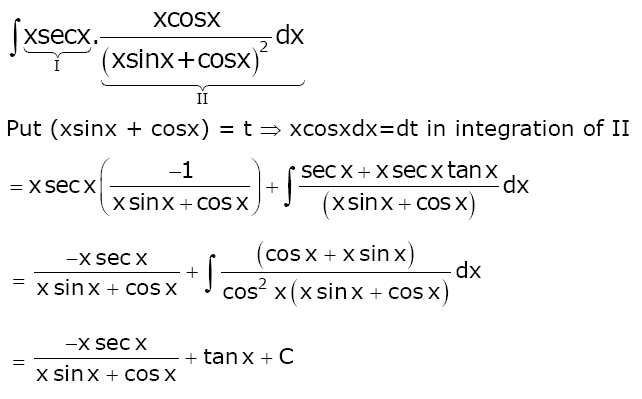


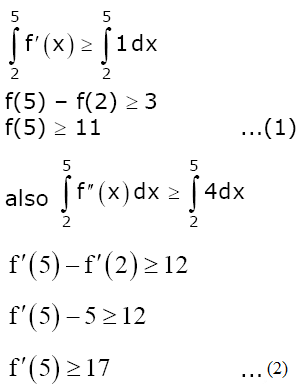

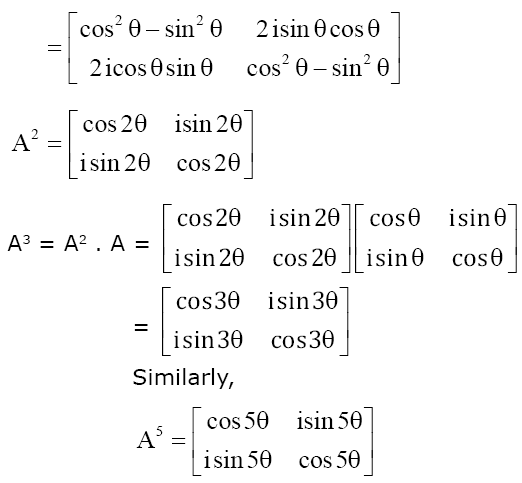




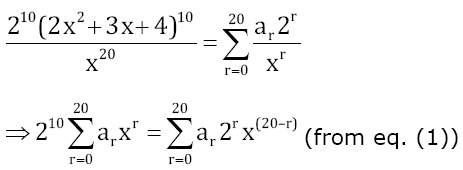




Comments