The admit card has been released KEAM 2017 by the Commissionerate of Entrance Examinations which can be downloaded from Official Website. The KEAM – is now conducting admissions, particularly to Pharmacy and Engineering courses. Earlier admission was conducted to Engineering, Medical and Agriculture courses across various colleges for Kerala.
The students can now download their admit cards by logging into the candidate’s profile through the link in an official website that is currently active now.
Guidelines to Download KEAM Admit Card
- Visit the official Website
- Click on a link displaying KEAM Admit Card download.
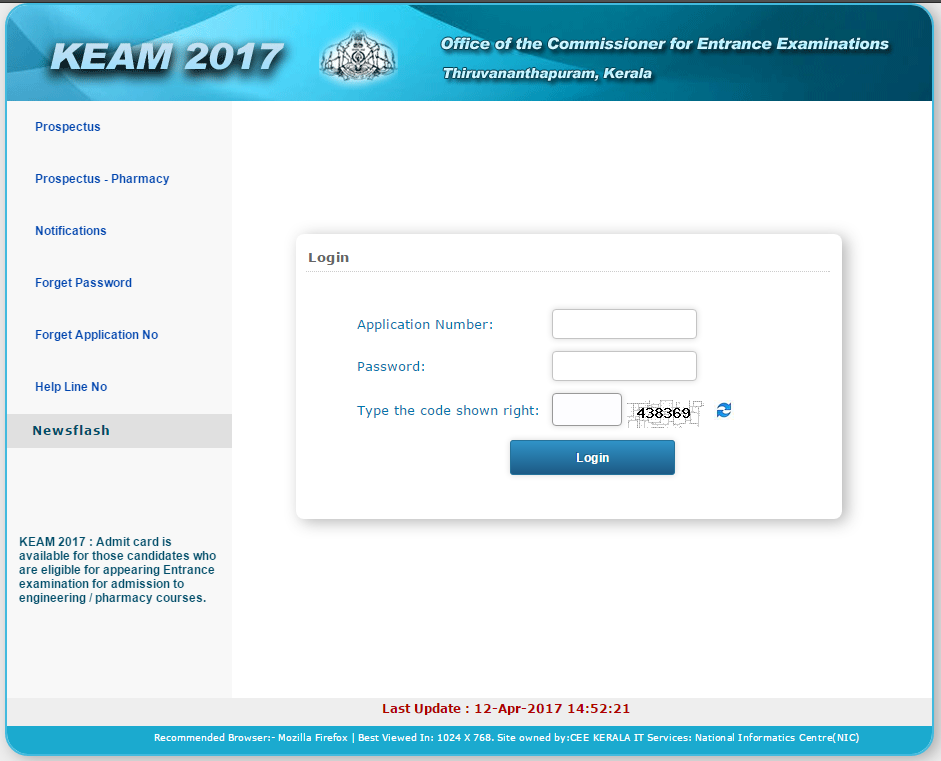
- Now click on the related link “admit card download “, click on KEAM 2017 Candidate Portal appearing on the new page.
- Enter the required details to log in to your account. The details encompass one’s password that was created during the time of registration, application number and security code provided on the screen.
- Now click on a menu button displaying ” admit card” and download the admit card.
The candidates should ensure to take a colour printout of the admit card as the candidates will not be allowed to enter the examination hall without it.
In certain cases, admit cards will be withheld for some candidates due to some issues with the thumbnail, signature image or photographs uploaded by them. These issues will be notified on the screen at the time of downloading the admit card. Such candidates should upload the relevant details through a relevant link provided on the website.
Examination Centers And Schedule
The centre for Kerala Engineering/Pharmacy Entrance Exam 2017 has been labelled in Dubai, New Delhi, Mumbai and different cities in Kerala. The examination will be held across labelled centres.
Comments