When we talk about the moment of inertia of a disk we can say that it is quite similar to that for a solid cylinder with any given measure of length. However, for a disk, we have to take it as a special character. Generally, it is used as a base for building the moment of inertia expression for different other shapes, such as a cylinder or a sphere.
Meanwhile, we can also find the moment of inertia of a circular disc with respect to different situations. They are as follows;
1. Solid disk
Here the axis of rotation is the central axis of the disk. It is expressed as;
| (½)MR2 |
2. Axis at Rim
In this case, the axis of rotation of a solid disc is at the rim. It is given as;
| 3/2 MR2 |
3. Disc With a Hole
Here the axis will be at the centre. It is expressed as;
| ½ M (a2 + b2) |
Moment Of Inertia Of A Disk Derivation
In order to explain how to calculate the moment of inertia of a disk, we will take the example of a uniform thin disk which is rotating about an axis through its centre.
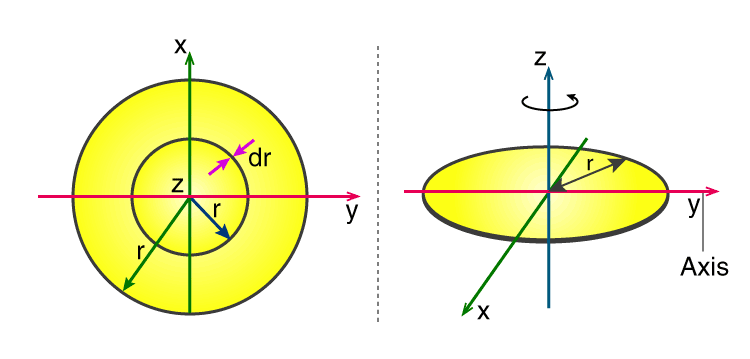
In the figure, we can see a uniform thin disk with radius r rotating about a Z-axis passing through the centre.
As we have a thin disk, the mass is distributed all over the x and y plane. Then, we move on to establishing the relation for surface mass density (σ) where it is defined as or said to be the mass per unit surface area. Since the disk is uniform, therefore, the surface mass density will also be constant where;
σ= m / A
or
σA=m
so
dm=σ(dA)
Now it is time for the simplification of the area where it can be assumed the area to be made of a collection of rings that are mostly thin in nature. The thin rings are said to be the mass increment (dm) of radius r which are at equal distance from the axis. The small area (dA) of every ring is further expressed by the length (2πr) times the small width of the rings (dr.) It is given as;
A = πr2, dA = d(πr2) = πdr2 = 2rdr
Now, we add all the rings from a radius range of 0 to R to get the full area of the disk. The radius range that is given is the value that is used in the integration of dr. If we put all these together then we get;
I = O∫R r2σ(πr)dr
I = 2 π σO∫R r3dr
I = 2 πσ r4 / 4 |oR
I = 2 πσ (R4 / 4 – 0)
I = 2 π (m / 4 )(R4 / 4)
I = 2 π (m / π r2 )(R4 / 4)
I = ½ mR2
This expression clearly proves all that we have discussed so far.
⇒ Check Other Object’s Moment of Inertia:
- Moment Of Inertia Of An Annular Disc
- Moment Of Inertia Of Circle
- Moment Of Inertia Of A Sphere
- Moment Of Inertia Of Triangle
- Moment Of Inertia Of Rod
Parallel Axis theorem


Comments