Moment of Inertia

Moment of inertia is an important topic and appears in most of the Physics problems involving mass in rotational motion. Usually, MOI is used to calculate angular momentum. We will learn more about this topic in the following paragraphs.

JEE Main 2021 LIVE Physics Paper Solutions 24-Feb Shift-1 Memory-based

What Is the Moment of Inertia?

The moment of inertia is defined as the quantity expressed by the body resisting angular acceleration, which is the sum of the product of the mass of every particle with its square of the distance from the axis of rotation. Or, in more simple terms, it can be described as a quantity that decides the amount of torque needed for a specific angular acceleration in a rotational axis. The moment of inertia is also known as the angular mass or rotational inertia. The SI unit of moment of inertia is kg m².

The moment of inertia is usually specified with respect to a chosen axis of rotation. It mainly depends on the distribution of mass around an axis of rotation. MOI varies depending on the axis that is chosen.

Table of Contents

• Formula
• Factors Affecting MOI
• Moment of Inertia of System of Particles
• For Rigid Bodies
• Calculation
• Moment of Inertia for Different Objects
• Parallel Axis Theorem
• Radius of Gyration
• Solved Examples
• Moment of Inertia of Different Shapes and Objects

Moment of Inertia Formula

In general form, moment of inertia is expressed as I = m × r² 

where,

m = Sum of the product of the mass.

r = Distance from the axis of the rotation.

And, integral form: I = ∫dI = ∫₀^M r² dm

⇒ The dimensional formula of the moment of inertia is given by, M¹ L² T⁰.

The role of the moment of inertia is the same as the role of mass in linear motion. It is the measurement of the resistance of a body to a change in its rotational motion. It is constant for a particular rigid frame and a specific axis of rotation.

Moment of inertia, I = ∑m_i r_i². . . . . . . (1)

Kinetic energy, K = ½ I ω² . . . . . . . . . (2)

What Are the Factors on Which the Moment of Inertia Depends?

The moment of inertia depends on the following factors:

• The density of the material
• Shape and size of the body
• Axis of rotation (distribution of mass relative to the axis)

We can further categorise rotating body systems as follows:

1. Discrete (System of particles)
2. Continuous (Rigid body)

Also Read:

• Area Moment of Inertia
• Polar Moment of Inertia
• Mass Moment of Inertia

Moment of Inertia of a System of Particles

The moment of inertia of a system of particles is given by,

I = ∑ m_i r_i² [from equation (1)]

where r_i is the perpendicular distance from the axis to the ith particle, which has mass m_i.

Example:

Moment of Inertia of Rigid Bodies

The moment of inertia of continuous mass distribution is found by using the integration technique. If the system is divided into an infinitesimal element of mass ‘dm’, and if ‘x’ is the distance from the mass element to the axis of rotation, the moment of inertia is:

I = ∫ r² dm . . . . . . (3)

Calculation of Moment of Inertia

A step-by-step guide to calculate the moment of inertia is given below:

Moment of Inertia of a Uniform Rod about a Perpendicular Bisector

Consider a uniform rod of mass M and length L, and the moment of inertia should be calculated about the bisector AB. Origin is at 0.

The mass element ‘dm’ considered is between x and x + dx from the origin.

As the rod is uniform, mass per unit length (linear mass density) remains constant.

∴  M/L = dm/dx

dm = (M/L)dx

Moment of inertia of dm,

dI = dm x²

dI = (M/L) x².dx

I =_-L/2 ∫^+L/2 dI = M/L × _-L/2∫^+L/2 x² dx

Here, x = -L/2 is the left end of the rod and ‘x’ changes from –L/2 to +L/2, the element covers the entire rod.

I = M/L × [x³/3]^+L/2_-L/2

I = ML²/12.

Therefore, the moment of inertia of a uniform rod about a perpendicular bisector (I) = ML²/12.

Moment of Inertia of a Circular Ring about Its Axis

Consider the line perpendicular to the plane of the ring through its centre. The radius of the ring is taken as R and its mass as M. All the elements are at the same distance from the axis of rotation, R.

Linear mass density is constant.

∴ M/2π = dm/dθ

dm = M/2π × dθ

I = ∫ R² dm = R² ₀∫^2π [M/2π] dθ

Limits: θ = 0 to 2π includes the whole mass of the ring

∴ I = R² [M/2π] × [θ]^2π₀

Therefore, the moment of inertia of a circular ring about its axis (I) = MR².

⇒ Note that in one-dimensional bodies, if it’s uniform, their linear mass density (M/L) remains constant. Similarly, for 2D and 3D, M/A (surface density) and M/V (volume density) remain constant, respectively.

⇒ Know the relation between torque and moment of inertia here

Moment of Inertia of a Rectangular Plate about a Line Parallel to an Edge and Passing through the Centre

The mass element can be taken between x and x + dx from the axis AB.

As the plate is uniform, M/A is constant.

M/A = dm/da

M/[l×b] = dm/dx.b

dm = (M/lb) × b × dx = (M/l) dx

I = ∫ x² dm = (M/l) × _-l/2∫^+l/2 [x²] dx

Limits: The left end of the rectangular plate is at x = -l/2, and the whole plate is covered by taking x from x = -l/2 to x = +l/2.

I = (M/l) [x³/3]_-l/2^+l/2 = Ml²/12

Therefore, the moment of inertia of a rectangular plate about a line parallel to an edge and passing through the centre (I) =  Ml²/12.

⇒ Note: If the mass element is chosen parallel to the length of the plate, then the moment of inertia would be, I = Mb²/12.

Moment of Inertia of a Uniform Circular Plate about Its Axis

Let the mass of the plate be M and the radius be R. The centre is at O, and the axis is perpendicular to the plane of the plate. The mass element considered is a thin ring between x and x+dx with thickness dx and mass dm.

As the plane is uniform, the surface mass density is constant.

M/A = dm/da

M/πR² = dm/[2π.x.dx]

I = ∫ x² dm = 2M/R² × ₀∫^R _x³ . dx

Limits: As we take the area of all mass elements from x = 0 to x = R, we cover the whole plate.

I = (2M/R²)[x⁴/4]^R₀ = (2M/R²) × R⁴/4 = MR²/2

Therefore, the moment of inertia of a uniform circular plate about its axis (I) = MR²/2.

Moment of Inertia of Thin Spherical Shell or Uniform Hollow Sphere

Let M and R be the mass, and the radius of the sphere, O at its centre and OY be the given axis. The mass is spread over the surface of the sphere, and the inside is hollow.

Let us consider the radii of the sphere at an angle θ and at an angle θ+dθ with the axis OY and the element (thin ring) of mass dm with radius Rsinθ is taken, as we rotate these radii about OY. The width of this ring is Rdθ, and its periphery is 2πRsinθ.

As the hollow sphere is uniform, the surface mass density (M/A) is constant.

M/A = dm/da

(M/4πR²)= dm/[2π × Rsinθ . Rdθ]

dm = [M/4πR²] × 2πR² . sinθ dθ = [M/2] × sinθ dθ

I = ∫ x² dm = ₀∫^π (R sin θ)² × [M/2] sinθ dθ

Limits: As θ increases from 0 to π, the elemental rings cover the whole spherical surface.

I = [MR²/2] × ₀∫^π sin³ θ dθ = MR²/2 × ₀∫^π [sin² θ . sin θ] × dθ

= [MR²/2] ₀∫^π (1 – cos² θ) sin θ × dθ

Now, on integrating the above equation by the substitution method, we get,

Take u = cos θ dθ

Then, du = – sin θ dθ

Changing limits, when θ = 0, u = 1

When, θ = π, u = -1

I = [MR²/2] × ₁∫^-1 (1 – u²) (-du)

= [MR²/2] × ₁∫^-1 (u² – 1) (du)

= [MR²/2] × [u³/3 – u]₁^-1

= [MR²/2] [-2/3 + 2] = [MR²/2 ]× [4/3] = 2MR²/3

Therefore, the moment of inertia of the thin spherical shell and uniform hollow sphere (I) = 2MR²/3.

Moment of Inertia of a Uniform Solid Sphere

Let us consider a sphere of radius R and mass M. A thin spherical shell of radius x, mass dm and thickness dx is taken as a mass element. Volume density (M/V) remains constant as the solid sphere is uniform.

M/V = dm/dV

M/[4/3 × πR³] = dm/[4πx².dx]

dm = [M/(4/3 × πR³) ]× 4πx² dx = [3M/R³] x² dx

I = ∫ dI = (2/3) × ∫ dm . x²

= (2/3) × ∫ [3M/R³ dx] x⁴

=( 2M/R³)× ₀∫^R x⁴ dx

Limits: As x increases from 0 to R, the elemental shell covers the whole spherical surface.

I = (2M/R³)[x⁵/5]^R₀

= (2M/R³)× R⁵/5

Therefore, the moment of inertia of a uniform solid sphere (I) = 2MR²/5.

Moment of Inertia for Different Objects

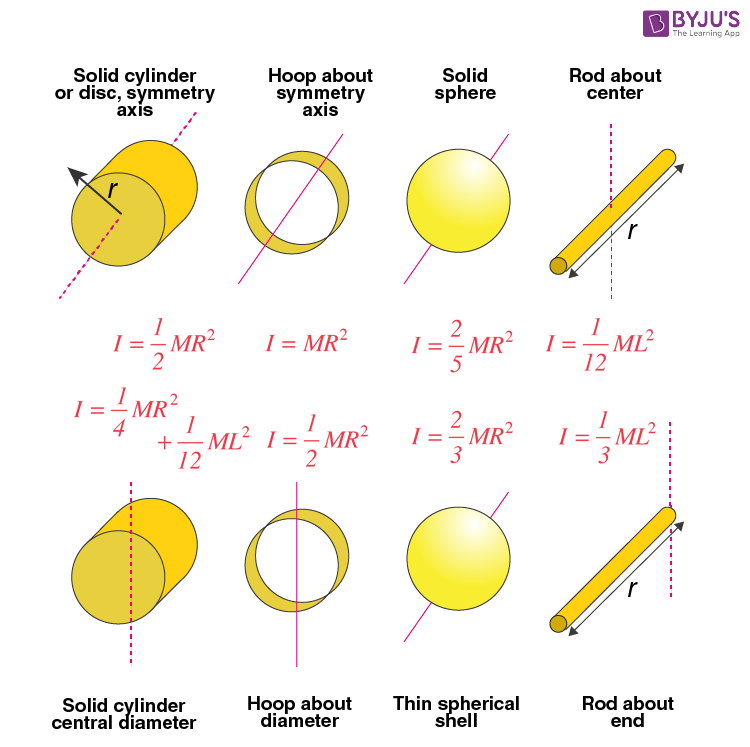
As we observed in the table above, the moment of inertia depends upon the axis of rotation. Whatever we have calculated so far is the moment of inertia of those objects when the axis is passing through their centre of masses (I_cm). Having chosen two different axes, you will observe that the object resists the rotational change differently. Therefore, to find the moment of inertia through any given axis, the following theorems are useful:

• Parallel Axis Theorem
• Perpendicular Axis Theorem

Parallel Axis Theorem

The moment of inertia of an object about an axis through its centre of mass is the minimum moment of inertia for an axis in that direction in space. The moment of inertia about an axis parallel to that axis through the centre of mass is given by,

I = I_cm + Md²

Where d is the distance between the two axes.

⇒ Read more on the Parallel and Perpendicular axis theorem

Radius of Gyration

The moment of inertia (I) of a body of mass m about an axis can be written in the form:

I = Mk²

Here, k is called the radius of gyration of the body about the given axis. It represents the radial distance from the given axis of rotation where the entire mass of the body can be assumed to be concentrated so that its rotational inertia remains unchanged.

The radius of gyration for a solid sphere about its axis is:

Mk² = 2MR²/5, or k = √[2/5] × R.

Solved Example

1. From a uniform circular disc of radius R and mass 9 M, a small disc of radius R/3 is removed, as shown in the figure. Calculate the moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through the centre of the disc.

Solution:

The moment of inertia of the removed part about the axis passing through the centre of mass and perpendicular to the plane of the disc = I_cm + md²

= [m × (R/3)²]/2 + m × [4R²/9] = mR²/2

Therefore, the moment of inertia of the remaining portion = moment of inertia of the complete disc – moment of inertia of the removed portion

= 9mR²/2 – mR²/2 = 8mR²/2

Therefore, the moment of inertia of the remaining portion (I _remaining) = 4mR².

2. Moment  Two balls connected by a rod, as shown in the figure below (Ignore the rod’s mass). The mass of ball X is 700 grams, and the mass of ball Y is 500 grams. What is the moment of inertia of the system about AB?

Given

The rotation axis is AB

m_X = 700 grams = 0.7 kg

m_Y = 500 grams = 0.5 kg

r_X = 10cm = 0.1m

r_Y = 40cm = 0.4m

Solution: 

I = m_X r_X² + m_Y r_Y²

I = (0.7)× (0.1)² + (0.5)× (0.4)²

I = (0.7) x (0.01) + (0.5) x (0.16)

I = 0.007 + o.08

I = 0.087 kg m²

Therefore, the moment of inertia of the system is 0.087 kg m².

3. Two balls are connected by a rod, as shown in the figure below (Ignore the rod’s mass). What is the moment of inertia of the system?

Given

m_X = 300 grams = 0.3 kg

m_Y = 500 grams = 0.5 kg

r_X = 0cm = 0m

r_Y = 30cm = 0.3m

Solution:

I = m_X r_X² + m_Y r_Y²

I = (0.3)× (0)² + (0.5)× (0.3)²

I = 0 + 0.045

I = 0.045 kg m²

Therefore, the moment of inertia of the system is 0.045kg m².

4. The mass of each ball is 200 grams, and connected by a cord. The length of the cord is 80 cm, and the width of the cord is 40 cm. What is the moment of inertia of the balls about the axis of rotation (Ignore cord’s mass)?

Given

Mass of ball = m₁ = m₂ = m₃ = m₄ = 200 gram = 0.2kg

Distance between the ball and the axis of rotation (r₁) = 40cm = 0.4 m

Distance between ball 2 and the axis of rotation (r₂) = 40 cm = 0.4 m

Distance between ball 3 and the axis of rotation (r₂) = 40 cm = 0.4 m

Distance between ball 4 and the axis of rotation (r₂) = 40 cm = 0.4 m

Solu:

I = m₁ r₁² + m₂ r₂² + m₃ r₃² + m₄ r₄²

I = (0.2) × (0.4)² + (0.2) × (0.4 )² + (0.2) × (0.4)² + (0.2) × (0.4)²

I = 0.032 + 0.032 + 0.032 + 0.032

I = 0.128 kg m²

Moment of inertia of the balls about the axis o.128 kg m²

Moment of Inertia of Different Shapes and Objects

Here is a list of the MOI of different shapes and objects.