Moment of inertia of a circle or the second-moment area of a circle is usually determined using the following expression;
| I = π R4 / 4 |
Here, R is the radius and the axis is passing through the centre. This equation is equivalent to I = π D4 / 64 when we express it taking the diameter (D) of the circle.
Similarly, a circle’s moment of inertia about an axis tangent to the circumference is given by;
| I = 5 π R4 / 4 |
The polar moment of inertia of a circle is expressed as;
| I = 5 π R4 / 2 |
Semi Circle
For a semi-circle the formula is given as;
| I = π R4 / 8 |
Quarter Circle
For a quarter circle the equation is expressed as;
| I = π R4 / 16 |
For the full derivation of the equations, students can visit the given links.
| Moment of Inertia Of a Semicircle |
| Moment of Inertia Of a Quarter Circle |
Moment Of Inertia Of Circle Derivation
For the derivation of the moment of inertia formula of a circle, we will consider the circular cross-section with the radius and an axis passing through the centre. In this derivation, we have to follow certain steps.
- Define the coordinate system.
- Find the differential area
- Integration
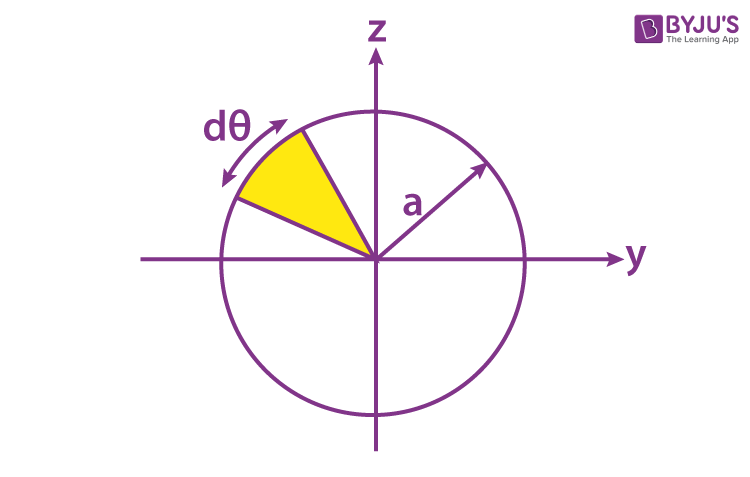
1. We will first begin with recalling the expression for the second-moment area. It is given as;
Iy = ∫A∫ z2dy dz
Iy = ∫ z2 da
Now we define the coordinates using the polar system. We get;
z = r sin θ
y = r cos θ
2. After this, we have to determine the differential area which is obtained by stating the area of the sector. It is given as;
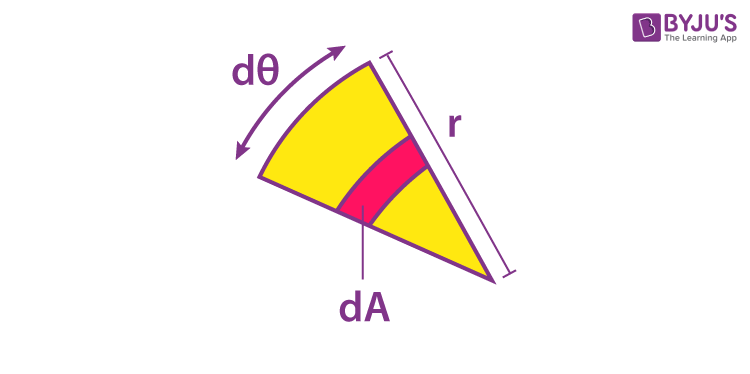
Area of the sector, A = ½ r2 dθ
We now carry out the differentiation and obtain;
dA =rdrd θ
3. We then write the integral for the moment of inertia of a circle. It is stated as;
Iy = o∫2πo∫r (r sin θ)2 rdrdr θ
We have to solve this.
Iy = o∫2πo∫r r3 sin2θ drd θ
Iy = o∫2π sin2θ [ o∫r r3dr ] d θ
Iy = o∫2π sin2θ [ r4 / 4]or d θ
Iy = r4 / 4 o∫2π sin2θ
Now we apply the trigonometric identity: sin2θ = 1-cos 2 θ / 2 and calculate the integral. It will be;
Iy = r4 / 4 o∫2π 1-cos 2 θ / 2 X d θ
Iy = r4 / 4 o∫2π ½ – ½ cos (2 θ) d θ
Iy = r4 / 4 [ ½ θ – ½ sin(2 θ)]o2π
Iy = r4 / 4 [ ½ (2π) – ¼ sin(4π) – ½ (0) + ¼ sin (0)]o2π
Iy = r4 / 4 (π – 0 – 0 + 0)
Iy = πr4 / 4
This equation also stands valid for the x-axis and similar derivation can be followed. In addition, the concept that we have discussed above can be further extended to find or determine the moment of inertia of a semicircle and a quarter circle.
Meanwhile, if we want to determine the M.O.I of the circle with respect to its axis tangent to the circumference we use the parallel axis theorem.
The theorem states;
II = I + Ad2
In this case, we have to consider,
d=R, A = πR2, I = πR4 / 4
If we apply the theorem we get;
II = πR4 / 4 + πR2 R2
II = 5 π R4 / 4
⇒ Check Other Object’s Moment of Inertia:
- Moment Of Inertia Of A Cylinder
- Moment Of Inertia Of A Disc
- Moment Of Inertia Of An Annular Disc
- Moment Of Inertia Of A Sphere
- Moment Of Inertia Of Ring
Parallel Axis Theorem


Comments