Area moment of inertia, also known as second area moment or 2nd moment of area, is a property of a two-dimensional plane shape, where it shows how its points are dispersed in an arbitrary axis in the cross-sectional plane. This property basically characterises the deflection of the plane shape under some load.
Area moment of inertia is usually denoted by the letter I for an axis in a plane. It is also denoted as J when the axis lies perpendicular to the plane. The dimension unit of the second area moment is Length to the power of four which is given as L4. If we take the International System of Units, its unit of dimension is a metre to the power of four or m4. If we take the Imperial System of Units, it can be inches to the fourth power, in4.
We will come across this concept in the field of structural engineering often. Here, the area moment of inertia is said to be the measure of the flexural stiffness of a beam. It is an important property that is used to measure the resistance offered by a beam to bending or in calculating a beam’s deflection. Here, we have to look at two cases.
- First, a beam’s resistance to bending can be easily described or defined by the planar second moment of the area, where the force lies perpendicular to the neutral axis.
- Secondly, the polar second moment of the area can be used to determine the beam’s resistance when the applied moment is parallel to its cross-section. It is basically the beam’s ability to resist torsion.
Area Moment of Inertia Formulas
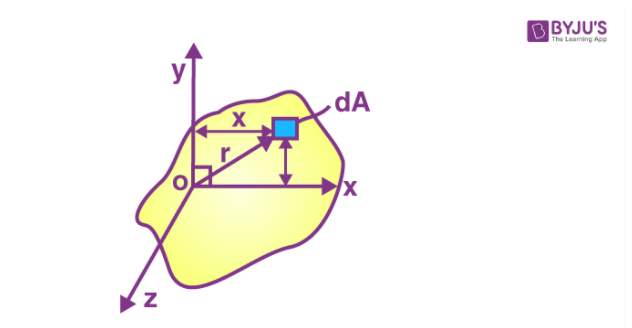
If we consider the second moment of area for the x-axis, then it is given as,
Meanwhile, the “product” moment of area is defined by
Determining Area Moment of Inertia
Parallel Axis Theorem

The moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis that passes through the centre of mass and the product of its mass and the square of the distance between the two lines.
I = Ig + Md2
M = Mass of the body
D = The perpendicular distance between the two lines
Perpendicular Axis Theorem
For the planar body, the moment of inertia about a perpendicular axis is equal to the sum of the moment of inertia about two perpendicular axes concurrent with this perpendicular axis, and it lies on the plane of the body. It is given by the expression,
IZ = Ix + Iy
Area Moments of Inertia for Some Common Shapes
Here is a list of area moments of inertia of some shapes.
| Shape/ Figure | Description of the Axis | Area Moments of Inertia |
| Rectangle | Centroid along the Cartesian Axis | \(\begin{array}{l}\begin{bmatrix} \frac{1}{2}ab^{3} & 0\\ 0 & \frac{1}{2}a^{3}b \end{bmatrix}\end{array} \) |
| Square | Centroid along the Cartesian Axis | \(\begin{array}{l}\begin{bmatrix} \frac{1}{12}a^{4} & 0\\ 0 & \frac{1}{12}a^{4} \end{bmatrix}\end{array} \) |
| Disk | Centroid | \(\begin{array}{l}\begin{bmatrix} \frac{1}{4}\Pi a^{4} & 0\\ 0 & \frac{1}{4}\Pi a^{4} \end{bmatrix}\end{array} \) |
| Ellipse | Centroid | \(\begin{array}{l}\begin{bmatrix} \frac{1}{4}\Pi ab^{3} & 0\\ 0 & \frac{1}{4}\Pi a^{3}b \end{bmatrix}\end{array} \) |
| Annulus | Centroid | \(\begin{array}{l}\begin{bmatrix} \frac{1}{4}\left (a^{4} – b^{4} \right )\Pi & 0\\ 0 & \frac{1}{4}\left (a^{4} – b^{4} \right )\Pi \end{bmatrix}\end{array} \) |
Parallel Axis Theorem


Comments