Moment of Inertia of a ring can be determined using various expressions. It includes;

• When the axis is passing through the centre (z-axis) and is perpendicular to it. For this we use;

• Along the axis which passes through the diameter. For this we have;

We will further look at how the equations are derived.

Moment Of Inertia Of Ring Formula Derivation

We will derive the moment of inertia of a ring for both instances below.

1. First, we will look at a ring about its axis passing through the centre.

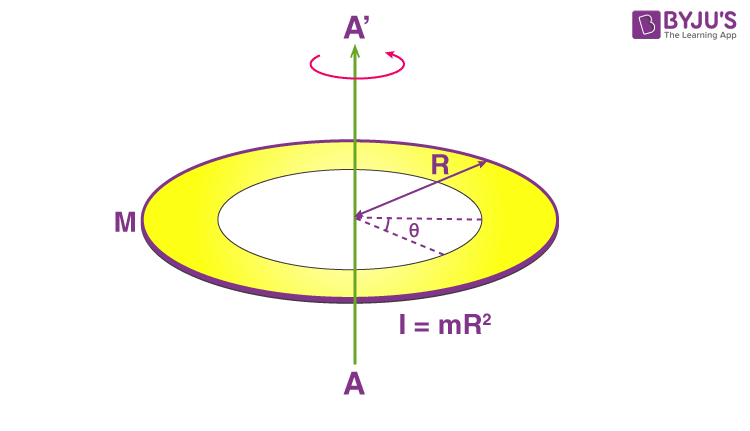
We will assume the mass of the ring to be M and radius be R.

Now we need to cut an elemental ring (dx) at the circumference of the ring. Hence, the mass (dm) of the elemental ring will be;

dm = (m / 2πR) dx

Next, we calculate dI = (dm) R²

dI =  [(m / 2πR) dx]R²

Substituting the values, we get;

dI = (m / 2πR) R² dx

Using integration;

I = (m R/ 2π) _o∫^2πR dx

I = (m / 2π) [x] ₀^2πR

I = (mR/2π) [2πR – 0]

I = mR²

2. For the second expression, we will be dealing with the moment of inertia of a ring about an axis passing through its diameter.

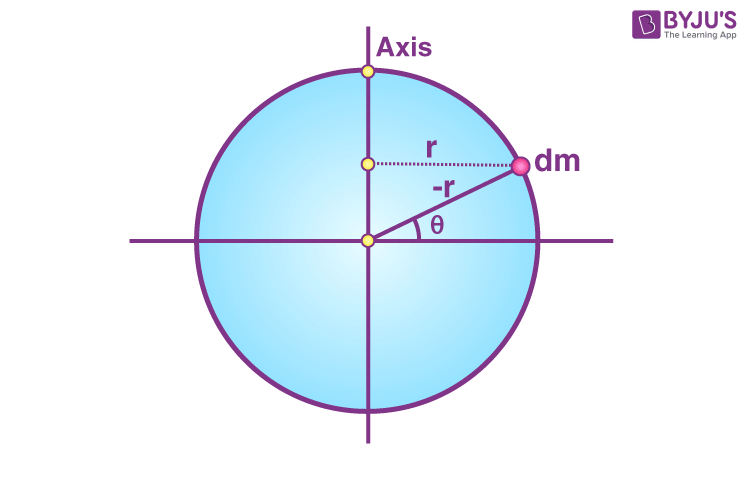
Here we will recall the formula;

I = ∫ r′²dm

We need to find dm. We will get;

dm = M / 2π dθ

Meanwhile, r′ = r cos θ

The next step is to carry out the integration. We will have;

I = _o∫^2π r² cos² θ (M / 2π) dθ

I = Mr² / 2π _o∫^2π cos² θ dθ

I = Mr² / 2π [θ / 2 + sin 2 θ / 4] |_o^2π

I = Mr² / 2π [ ( π + 0) – (0 + 0)]

I = Mr² / 2

⇒ Check Other Object’s Moment of Inertia:

• Moment Of Inertia Of Circle
• Moment Of Inertia Of A Quarter Circle
• Moment Of Inertia Of Semicircle
• Moment Of Inertia Of A Sphere
• Moment Of Inertia Of A Disc